1ICFO-Institut de Ciencies Fotoniques, Barcelona teaduse ja tehnoloogia instituut, 08860 Castelldefels, Hispaania
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Hispaania
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Prantsusmaa
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Hispaania
Kas see artikkel on huvitav või soovite arutada? Scite või jätke SciRate'i kommentaar.
Abstraktne
Vastastikku erapooletud alused vastavad kvantinformatsiooni teoorias väga kasulikele mõõtepaaridele. Väikseimas liitmõõtmes, kuues, on teada, et eksisteerib kolm kuni seitse vastastikku erapooletut alust ning aastakümneid vana oletus, mida tuntakse Zauneri oletusena ja mis väidab, et neid on kõige rohkem kolm. Siin käsitleme Zauneri oletusi arvuliselt, konstrueerides Belli võrratused iga täisarvude paari $n,d ge 2$ jaoks, mida saab maksimaalselt rikkuda dimensioonis $d$ siis ja ainult siis, kui selles dimensioonis on $n$ MUB. Seetõttu muudame Zauneri oletuse optimeerimisprobleemiks, mida käsitleme kolme numbrilise meetodi abil: kiik-optimeerimine, mittelineaarne poolmääratletud programmeerimine ja Monte Carlo tehnikad. Kõik kolm meetodit tuvastavad õigesti teadaolevad juhtumid madalates mõõtmetes ja kõik viitavad sellele, et kuues dimensioonis ei eksisteeri nelja vastastikku erapooletut alust, kusjuures kõik leiavad samad alused, mis arvuliselt optimeerivad vastavat Belli ebavõrdsust. Veelgi enam, need arvulised optimeerijad näivad langevat kokku kuuenda mõõtme „nelja kõige kaugema alusega”, mis leiti kauguse mõõtmise arvulise optimeerimise kaudu punktis [P. Raynal, X. Lü, B.-G. Englert, {Phys. Rev. A}, { 83} 062303 (2011)]. Lõpuks näitavad Monte Carlo tulemused, et kümnes dimensioonis on maksimaalselt kolm MUB-i.
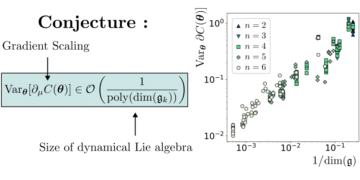
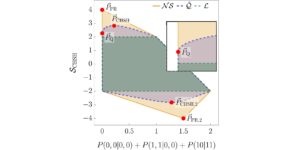
Esiletõstetud pilt: suhteline erinevus meie Belli ebavõrdsuse väärtuse, eeldades, et mõõtmes d on n MUB-i, ja meie arvuliste meetoditega leitud väärtuse vahel. Nullväärtused tähendavad, et meetodid leidsid dimensioonis d n MUB-i, samas kui nullist erinevad väärtused tähendavad, et meetodid ei leidnud dimensioonist d n MUB-i. Kõik teadaolevad juhtumid (dimensioonid kaks kuni viis ja mõõde kuus kahe ja kolme MUB-iga) on numbritega õigesti identifitseeritud. Kuuendas dimensioonis ei leia ükski meetoditest nelja MUB-i ja kõik meetodid koonduvad samasse nelja aluse komplekti.
Populaarne kokkuvõte
Vaatamata nende laialdasele kasutamisele on MUB-ide struktuuri kohta endiselt lahtisi küsimusi. Kõige silmatorkavam on see, et paarikaupa erapooletute mõõtmiste maksimaalne arv ("MUBide arv") pole teada, kui kvantsüsteemi mõõde on liitarv. Täpsemalt, kuuendas dimensioonis teame ainult seda, et MUB-ide arv on kolm kuni seitse. Pikaajaline avatud oletus on Zauneri oletus, mis väidab, et kuuendas dimensioonis pole rohkem kui kolm MUB-i. Seda aastakümnete pikkust oletust toetavad mõned arvulised tõendid, kuid tõendeid pole tänaseni.
Selles töös käsitleme Zauneri oletusi Belli mittepaiksuse kaudu. Belli mittepaiksus puudutab kahte eksperimenteerijat, kellel ei ole lubatud suhelda, kuid kes võivad jagada mõningaid korrelatsioone klassikalise juhuslikkuse või jagatud kvantoleku kujul. On näidatud, et kvantressursside jagamine võib viia eksperimentaalsete andmeteni, mida ei saa seletada klassikalise füüsikaga (täpsemalt nn lokaalsete varjatud muutujate mudelitega). Seda tuntakse Belli teoreemina ja seda on viimasel kümnendil katseliselt kontrollitud. Katseandmete mitteklassikalisuse tunnistajaks on kõige sagedamini nn Belli ebavõrdsus, mis on katses esinevate mõõtmistulemuste tõenäosuste funktsioonid. Klassikalised andmed peavad rahuldama Belli ebavõrdsust, samas kui kvantandmed võivad neid rikkuda.
Hiljuti on leitud Belli ebavõrdsusi, mida rikutakse maksimaalselt, kui üks osapooltest kasutab antud mõõtmega MUB-mõõtmiste paari. Selles töös laiendame neid ebavõrdsusi uutele, mida maksimaalselt rikub valitud arv MUB-i mõõtmisi antud mõõtmes. Veelgi enam, kui eksperimendi mõõde on fikseeritud, saavutatakse maksimaalne rikkumine siis ja ainult siis, kui kasutatud mõõtmised vastavad antud mõõtmes valitud MUB-ide arvule. Seetõttu on antud dimensioonis teatud arvu MUB-ide olemasolu otsustamine samaväärne vastava Belli ebavõrdsuse maksimaalse rikkumise leidmisega selles fikseeritud mõõtmes.
Kuigi selle maksimaalse rikkumise leidmine on üldiselt raske probleem, kasutame kolme erinevat numbrilist meetodit, et leida meie Belli ebavõrdsuse maksimaalne rikkumine fikseeritud mõõtmes. Kaks neist meetoditest on poolkindla programmeerimistehnika variandid, kolmas on aga inspireeritud statistilisest füüsikast ja seda nimetatakse simuleeritud lõõmutamiseks. Kuigi kõik need meetodid on heuristilised – see tähendab, et pole mingit garantiid, et nad leiavad probleemi tõelise optimumi –, saab nende toimivust hinnata, rakendades neid optimeerimisprobleemidele, mille optimum on teada. Eelkõige leiame, et kõik kolm meetodit suudavad MUB-i mõõtmisi õigesti tuvastada juhtudel, kui need on teadaolevalt olemas. Peale selle, juhtudel, kui neid teadaolevalt ei eksisteeri, lähenevad kõik kolm meetodit samale mõõtmiskomplektile kuni numbrilise täpsuseni. Seejärel rakendame oma meetodeid esimesele tundmatule juhtumile, st neljale MUB-ile kuues dimensioonis. Ükski meetoditest ei suuda tuvastada nelja MUB-i kuues dimensioonis, kuid jällegi lähenevad need kõik samale neljast mõõtmisest koosnevale komplektile kuni numbrilise täpsuseni. Lisaks ei leia simuleeritud lõõmutamise tehnika järgmises komposiitmõõtmes, kümnes mõõtmes, nelja MUB-i. Seetõttu, kuigi meie tehnikate heuristilise olemuse tõttu ei saa esitada rangeid väiteid, toetavad meie tulemused Zauneri oletust Belli mittepaiksuse uuest vaatenurgast.
► BibTeX-i andmed
► Viited
[1] ID Ivanovic. Kvantaalse oleku määramise geomeetriline kirjeldus. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kvantkrüptograafia: avaliku võtme jagamine ja müntide loopimine. IEEE rahvusvahelise arvutite, süsteemide ja signaalitöötluse konverentsi materjalid (IEEE, 1984), 175:8, 1984. doi: 10.1016/j.tcs.2011.08.039.
https:///doi.org/10.1016/j.tcs.2011.08.039
[3] Artur K. Ekert. Belli teoreemil põhinev kvantkrüptograafia. Phys. Rev. Lett., 67:661–663, 1991. doi: 10.1103/PhysRevLett.67.661.
https:///doi.org/10.1103/PhysRevLett.67.661
[4] Dagmar Bruß. Optimaalne pealtkuulamine kuue olekuga kvantkrüptograafias. Phys. Rev. Lett., 81:3018–3021, 1998. doi: 10.1103/PhysRevLett.81.3018.
https:///doi.org/10.1103/PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques ja Mohamed Bourennane. Kvant-jutujuurdepääsukoodid, kasutades üksikuid $d$-taseme süsteeme. Phys. Rev. Lett., 114:170502, 2015. doi: 10.1103/PhysRevLett.114.170502.
https:///doi.org/10.1103/PhysRevLett.114.170502
[6] Máté Farkas ja Jędrzej Kaniewski. Enesetestivad vastastikku erapooletud alused ettevalmistamise ja mõõtmise stsenaariumis. Phys. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https:///doi.org/10.1103/PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci ja N. Gisin. Bell ebavõrdsus binaarsete mõõtmistega kvintide jaoks. Kvantinfo. Comput., 3(2):157–164, 2003. doi: 10.26421/QIC3.2-6.
https:///doi.org/10.26421/QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos ja Remigiusz Augusiak. Maksimaalne mittelokaalsus maksimaalsest takerdumisest ja vastastikku erapooletutest alustest ning kahekvtritiliste kvantsüsteemide enesetestimine. Quantum, 3:198, 2019. doi: 10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal ja Jędrzej Kaniewski. Vastastikused erapooletud alused ja sümmeetrilised informatsiooniliselt täielikud mõõtmised Belli katsetes. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson ja Karol Życzkowski. Vastastikku erapooletutel alustel. International Journal of Quantum Information, 08(04):535–640, 2010. doi: 10.1142/S0219749910006502.
https:///doi.org/10.1142/S0219749910006502
[11] William K Wootters ja Brian D Fields. Optimaalse oleku määramine vastastikku erapooletute mõõtmiste abil. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan ja Thomas Beth. Uuskonstruktsioon vastastikku erapooletutest alustest ruudukujulistes mõõtmetes. Kvantinfo. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https:///doi.org/10.26421/QIC5.2-1
[13] Mihály Weiner. Lõhe vastastikku erapooletute aluste maksimaalse arvu jaoks. Proc. Amer. matemaatika. Soc., 141:1963–1969, 2013. doi: 10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Doktoritöö, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep ja Pawel Wocjan. Lie algebra vastastikku erapooletud alused ja ortogonaalsed dekompotsioonid. Kvantinfo. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https:///doi.org/10.26421/QIC7.4-6
[16] Stephen Brierley ja Stefan Weigert. Kuuendas dimensioonis vastastikku erapooletute aluste konstrueerimine. Phys. Rev. A, 79:052316, 2009. doi: 10.1103/PhysRevA.79.052316.
https:///doi.org/10.1103/PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi ja Mihály Weiner. Üldistatud Pauli probleem ja MUB-kolmikute lõpmatu perekond dimensioonis 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, mai 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer ja Afaq Tahir. Tõendid Zauneri MUB-oletuse poolt ja vastu dokumendis $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling ja Sven Polak. Vastastikused erapooletud alused: polünoomi optimeerimine ja sümmeetria. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej ja Karol Życzkowski. Vastastikuselt erapooletud alused ja kuuendat järku Hadamardi maatriksid. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https:///doi.org/10.1063/1.2716990
[21] Philippe Raynal, Xin Lü ja Berthold-Georg Englert. Kuues mõõtmes vastastikku erapooletud alused: neli kõige kaugemat baasi. Phys. Rev. A, 83:062303, 2011. doi: 10.1103/PhysRevA.83.062303.
https:///doi.org/10.1103/PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz ja Marcin Pawłowski. Ühendused vastastikku erapooletute aluste ja kvant juhusliku juurdepääsu koodide vahel. Phys. Rev. Lett., 121:050501, 2018. doi: 10.1103/PhysRevLett.121.050501.
https:///doi.org/10.1103/PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani ja Stephanie Wehner. Kella mittepaiksus. Rev. Mod. Phys., 86:419–478, 2014. doi: 10.1103/RevModPhys.86.419.
https:///doi.org/10.1103/RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API for C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe ja Kouhei Harada. Primaal-kahe sisepunkti meetod mittelineaarseks poolkindlaks programmeerimiseks. Matemaatiline programmeerimine, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https:///doi.org/10.1007/s10107-011-0449-z
[26] Stephen Boyd ja Lieven Vandenberghe. Kumer optimeerimine. Cambridge University Press, 2004. doi: 10.1017/CBO9780511804441.
https:///doi.org/10.1017/CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt ja MP Vecchi. Optimeerimine simuleeritud lõõmutamise teel. Science, 220 (4598): 671–680, 1983. doi: 10.1126/teadus.220.4598.671.
https:///doi.org/10.1126/science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller ja Edward Teller. Kiirarvutusmasinate olekuarvutuste võrrand. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https:///doi.org/10.1063/1.1699114
[29] Miguel Navascués, Stefano Pironio ja Antonio Acín. Kvantkorrelatsioonide hulga piiramine. Phys. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https:///doi.org/10.1103/PhysRevLett.98.010401
Viidatud
See raamat on avaldatud Quantum all Creative Commons Attribution 4.0 International (CC BY 4.0) litsents. Autoriõigus jääb algsetele autoriõiguste valdajatele, näiteks autoritele või nende institutsioonidele.