Uusi läpimurto tuo matriisikertomisen lähemmäksi ihannetta | Quanta-lehti

Tietojenkäsittelytieteilijät ovat vaativa joukko. Heille ei riitä, että saa oikean vastauksen ongelmaan – lähes aina tavoitteena on saada vastaus mahdollisimman tehokkaasti.

Kertokaa matriisit tai lukutaulukot. Vuonna 1812 ranskalainen matemaatikko Jacques Philippe Marie Binet keksi perussäännöt, joita opetamme edelleen opiskelijoille. Se toimii täydellisesti, mutta muut matemaatikot ovat löytäneet tapoja yksinkertaistaa ja nopeuttaa prosessia. Nyt tehtävänä nopeuttaa prosessia Matriisin kertolasku on matematiikan ja tietojenkäsittelytieteen risteyksessä, jossa tutkijat jatkavat prosessin parantamista tähän päivään asti – vaikka viime vuosikymmeninä saavutukset ovat olleet melko vaatimattomia. Vuodesta 1987 lähtien numeeriset parannukset matriisin kertomisessa ovat olleet "pieniä ja ... erittäin vaikeasti saavutettavissa", sanoi. François Le Gall, tietojenkäsittelytieteilijä Nagoyan yliopistossa.

Nyt kolme tutkijaa - Ran Duan ja Renfei Zhou Tsinghuan yliopistosta ja Hongxun Wu Kalifornian yliopistosta Berkeleystä - ovat ottaneet suuren askeleen eteenpäin hyökkääessään tätä ikuista ongelmaa vastaan. Heidän uusia tuloksia, joka esiteltiin viime marraskuussa Foundations of Computer Science -konferenssissa, johtuvat odottamattomasta uudesta tekniikasta, Le Gall sanoi. Vaikka parannus itsessään oli suhteellisen pieni, Le Gall kutsui sitä "käsitteellisesti suuremmiksi kuin muut aikaisemmat".

Tekniikka paljastaa aiemmin tuntemattoman ja siten hyödyntämättömän lähteen mahdollisille parannuksille, ja se on jo kantanut hedelmää: Toinen lehtiTammikuussa julkaistu julkaisu perustuu ensimmäiseen, joka osoittaa, kuinka matriisikertoa voidaan tehostaa entisestään.

"Tämä on merkittävä tekninen läpimurto", sanoi William Kuszmaul, teoreettinen tietotekniikan tutkija Harvardin yliopistosta. "Se on suurin parannus matriisin kertolaskussa, jonka olemme nähneet yli kymmeneen vuoteen."

Enter the Matrix

Se voi tuntua epäselvältä ongelmalta, mutta matriisikertominen on perustavanlaatuinen laskennallinen operaatio. Se on sisällytetty suureen osaan algoritmeja, joita ihmiset käyttävät päivittäin erilaisiin tehtäviin terävämmän tietokonegrafiikan näyttämisestä verkkoteorian logististen ongelmien ratkaisemiseen. Ja kuten muillakin laskennan aloilla, nopeus on ensiarvoisen tärkeää. Pienetkin parannukset voivat lopulta johtaa merkittäviin säästöihin aikaa, laskentatehoa ja rahaa. Mutta toistaiseksi teoreetikot ovat pääasiassa kiinnostuneita siitä, kuinka nopea prosessi voi koskaan olla.

Perinteinen tapa kertoa kaksi n-by-n matriisit - kertomalla ensimmäisen matriisin jokaisen rivin numerot toisen matriisin sarakkeiden luvuilla - vaatii n³ erilliset kertolaskut. 2 x 2 matriiseilla se tarkoittaa 2:ta³ tai 8 kertolaskua.

Vuonna 1969 matemaatikko Volker Strassen paljasti monimutkaisemman menetelmän, joka pystyi kertomaan 2 x 2 matriisit vain seitsemällä kertolaskuvaiheella ja 18 yhteenlaskolla. Kaksi vuotta myöhemmin tietojenkäsittelytieteilijä Shmuel Winograd osoitti, että seitsemän on todellakin ehdoton minimi 2 x 2 matriiseille.

Strassen hyödynsi samaa ideaa osoittaakseen, että kaikki suurempi n-by-n matriisit voidaan myös kertoa pienemmällä kuin n³ askeleet. Tämän strategian avainelementti sisältää prosessin, jota kutsutaan hajotukseksi – suuren matriisin hajottaminen peräkkäin pienemmiksi alimatriiseiksi, jotka voivat päätyä niinkin pieniksi kuin 2 x 2 tai jopa 1 x 1 (nämä ovat vain yksittäisiä lukuja).

Perustelut jättimäisen joukon jakamiselle pieniksi paloiksi ovat melko yksinkertaisia Virginia Vassilevska Williams, Massachusetts Institute of Technologyn tietojenkäsittelytieteilijä ja yhden uuden artikkelin toinen kirjoittaja. "Ihmisen on vaikea katsoa suurta matriisia (esim. luokkaa 100 x 100) ja ajatella parasta mahdollista algoritmia", Vassilevska Williams sanoi. Edes 3 x 3 matriiseja ei ole vielä täysin ratkaistu. "Voidaan kuitenkin käyttää nopeaa algoritmia, joka on jo kehitetty pienille matriiseille, jotta saadaan nopea algoritmi myös suuremmille matriiseille."

Avain nopeuteen, tutkijat ovat määrittäneet, on vähentää kertolaskuvaiheiden määrää alentamalla eksponenttia n³ (tavallinen menetelmä) niin paljon kuin pystyvät. Pienin mahdollinen arvo, n², on periaatteessa niin pitkä kuin vastauksen kirjoittaminen kestää. Tietojenkäsittelytieteilijät kutsuvat tätä eksponenttia nimellä omega, ω, with n^ω on pienin mahdollinen vaihe, joka tarvitaan kahden onnistuneeseen kertomiseen n-by-n matriisit kuten n kasvaa hyvin suureksi. "Tämän työn tarkoitus", sanoi Zhou, joka oli myös tammikuun 2024 paperin kirjoittaja, "on nähdä, kuinka lähelle kahta voit tulla ja voidaanko se saavuttaa teoriassa."

Laser Focus

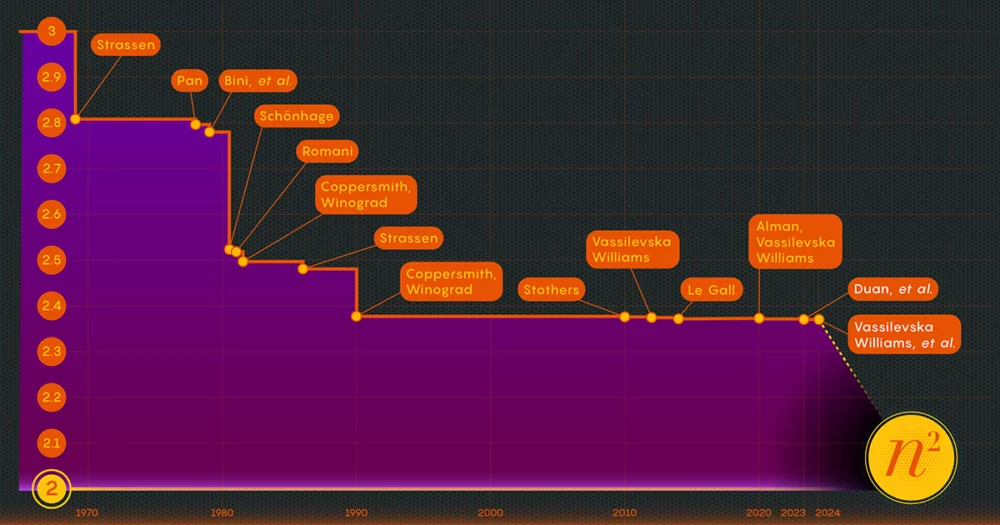
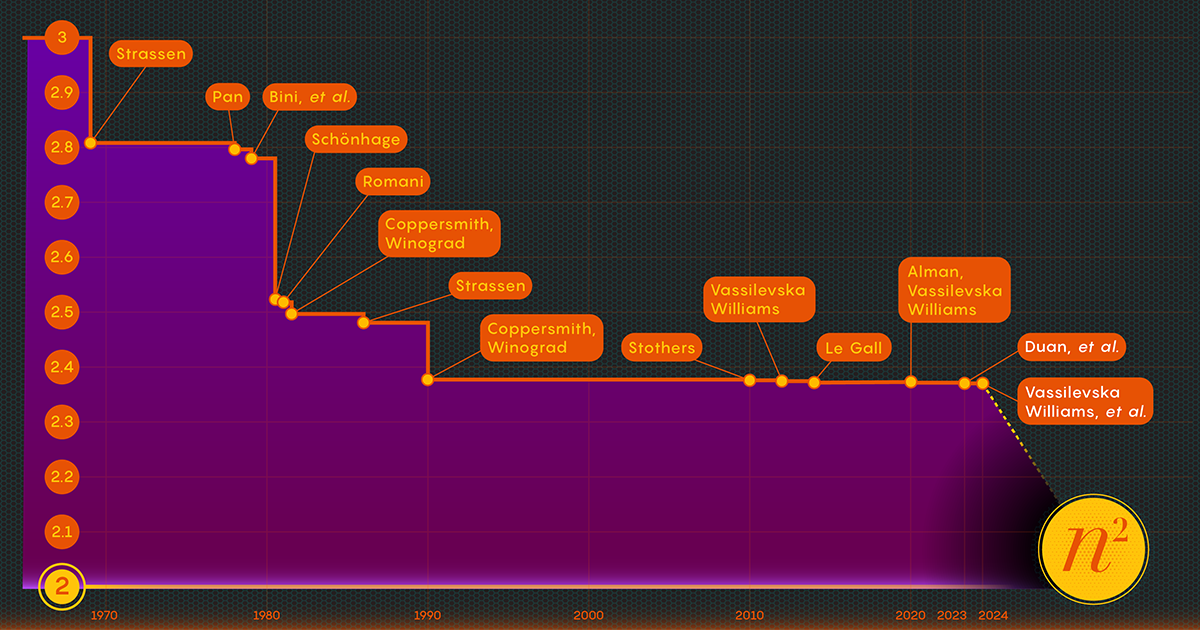
Vuonna 1986 Strassen teki toisen suuren läpimurron, kun hän käyttöön mitä kutsutaan lasermenetelmäksi matriisin kertolaskussa. Strassen käytti sitä määrittämään omegan yläarvon 2.48. Vaikka menetelmä on vain yksi askel suurissa matriisikertoloissa, se on yksi tärkeimmistä, koska tutkijat ovat jatkaneet sen parantamista.

Vuotta myöhemmin Winograd ja Don Coppersmith esittelivät uuden algoritmin, joka täydensi kauniisti lasermenetelmää. Tämä työkalujen yhdistelmä on esiintynyt käytännössä kaikissa myöhemmissä yrityksissä nopeuttaa matriisin kertomista.

Tässä on yksinkertaistettu tapa ajatella, kuinka nämä eri elementit sopivat yhteen. Aloitetaan kahdella suurella matriisilla, A ja B, jotka haluat kertoa yhdessä. Ensin jaat ne useiksi pienemmiksi alimatriiseiksi tai lohkoiksi, kuten niitä joskus kutsutaan. Seuraavaksi voit käyttää Coppersmithin ja Winogradin algoritmia eräänlaisena ohjekirjana lohkojen käsittelyyn ja lopulta kokoamiseen. "Se kertoo minulle, mitä kerrotaan ja mitä lisätään ja mitkä merkinnät menevät minne" tuotematriisissa C, Vassilevska Williams sanoi. "Se on vain resepti C:n rakentamiseen A:sta ja B:stä."

Siinä on kuitenkin saalis: joskus päädyt lohkoihin, joilla on yhteisiä merkintöjä. Näiden jättäminen tuotteeseen vastaisi kyseisten merkintöjen laskemista kahdesti, joten jossain vaiheessa sinun on päästävä eroon päällekkäisistä termeistä, joita kutsutaan päällekkäisiksi. Tutkijat tekevät tämän "tappaamalla" lohkot, joissa he ovat – asettamalla niiden komponentit nollaksi poistaakseen ne laskelmista.

Siellä Strassenin lasermenetelmä astuu vihdoin peliin. "Lasermenetelmä toimii tyypillisesti erittäin hyvin ja löytää yleensä hyvän tavan tappaa lohkojen osajoukko päällekkäisyyden poistamiseksi", Le Gall sanoi. Kun laser on poistanut tai "polttanut" kaikki päällekkäisyydet, voit muodostaa lopputuotematriisin, C.

Näiden erilaisten tekniikoiden yhdistäminen johtaa algoritmiin kahden matriisin kertomiseksi tarkoituksellisesti niukalla kertolaskumäärällä - ainakin teoriassa. Lasermenetelmää ei ole tarkoitettu käytännölliseksi; se on vain tapa ajatella ihanteellista tapaa kertoa matriiseja. "Emme koskaan suorita menetelmää [tietokoneella]", Zhou sanoi. "Analysoimme sen."

Ja tämä analyysi johti omegan suurimpaan parannukseen yli kymmeneen vuoteen.

Tappio löytyy

Viime kesän Duanin, Zhoun ja Wun paperi osoitti, että Strassenin prosessia voitaisiin vielä nopeuttaa merkittävästi. Se kaikki johtui käsitteestä, jota he kutsuivat piilotetuksi menetykseksi, joka on haudattu syvälle aikaisempiin analyyseihin - "se oli seurausta liian monien lohkojen tahattomasta tappamisesta", Zhou sanoi.

Lasermenetelmä toimii merkitsemällä päällekkäisiä lohkoja roskiksi, jotka on tarkoitettu hävitettäväksi; muut lohkot katsotaan kelvollisiksi ja ne pelastetaan. Valintaprosessi on kuitenkin jossain määrin satunnaistettu. Roskaksi luokiteltu lohko voi itse asiassa osoittautua hyödylliseksi. Tämä ei ollut täydellinen yllätys, mutta tutkimalla monia näistä satunnaisista valinnoista Duanin tiimi päätti, että lasermenetelmä aliarvioi järjestelmällisesti lohkoja: Lisää lohkoja pitäisi säästää ja vähemmän heittää pois. Ja kuten yleensä, vähemmän jätettä johtaa parempaan tehokkuuteen.

"Pystymys pitää enemmän lohkoja ilman päällekkäisyyttä johtaa siis … nopeampaan matriisin kertolaskualgoritmiin", Le Gall sanoi.

Todistettuaan tämän häviön olemassaolon Duanin tiimi muutti tapaa, jolla lasermenetelmä merkitsee lohkoja, mikä vähensi jätettä huomattavasti. Tämän seurauksena he asettivat omegan uudeksi ylärajaksi noin 2.371866:een, mikä on parannus aiempaan ylärajaan 2.3728596, asetettu vuonna 2020 Josh Alman ja Vassilevska Williams. Se saattaa tuntua vaatimattomalta muutokselta, mikä laskee rajaa vain noin 0.001:lla. Mutta se on suurin yksittäinen parannus, jonka tutkijat ovat nähneet vuoden 2010 jälkeen. Vertailun vuoksi Vassilevska Williamsin ja Almanin vuoden 2020 tulos parani edeltäjäänsä vain 0.00001.

Mutta tutkijoille jännittävintä ei ole vain itse uusi ennätys, joka ei kestänyt kauan. Se on myös se tosiasia, että lehti paljasti uuden parannustien, joka siihen asti oli jäänyt täysin huomaamatta. Lähes neljän vuosikymmenen ajan kaikki ovat luottaneet samaan lasermenetelmään, Le Gall sanoi. "Sitten he huomasivat, että no, voimme tehdä paremmin."

Tammikuun 2024 paperi tarkensi tätä uutta lähestymistapaa, jolloin Vassilevska Williams, Zhou ja heidän kirjoittajansa pystyivät edelleen vähentämään piilotettuja menetyksiä. Tämä johti omegan ylärajan lisäparannukseen, mikä pienensi sen arvoon 2.371552. Kirjoittajat myös yleistivät samaa tekniikkaa parantaakseen kertolaskuprosessia suorakaiteen (n-by-m) matriisit — menettely, jolla on sovelluksia graafiteoriassa, koneoppimisessa ja muilla aloilla.

Edistyminen näillä linjoilla on aivan varmaa, mutta rajoituksia on. Vuonna 2015 Le Gall ja kaksi yhteistyökumppania osoittautui että nykyinen lähestymistapa – lasermenetelmä yhdistettynä Coppersmith-Winogradin reseptiin – ei voi tuottaa omega-arvoa alle 2.3078:n. Lisäparannuksia varten Le Gall sanoi: "sinun on parannettava Coppersmithin ja Winogradin alkuperäistä [lähestymistapaa], joka ei ole oikeastaan ​​muuttunut vuoden 1987 jälkeen" Mutta toistaiseksi kukaan ei ole keksinyt parempaa tapaa. Ei ehkä ole edes yhtä.

"Omegan parantaminen on itse asiassa osa tämän ongelman ymmärtämistä", Zhou sanoi. ”Jos ymmärrämme ongelman hyvin, voimme suunnitella sille parempia algoritmeja. [Ja] ihmiset ovat vielä hyvin varhaisessa vaiheessa ymmärtämään tätä ikivanhaa ongelmaa.