Le modèle de mélange du procédé Dirichlet

• Le 23 juin 2014
• Vassilis Vryniotis
• . 2 Commentaires

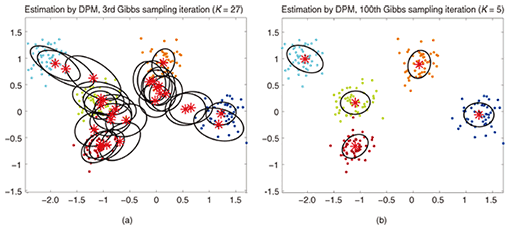
Ce billet de blog est la quatrième partie de la série sur Clustering avec les modèles de mélange de processus Dirichlet. Dans les articles précédents, nous avons discuté des modèles de mélange de Dirichlet fini et nous avons pris la limite de leur modèle pour les clusters k infinis, ce qui nous a conduit à l'introduction des processus de Dirichlet. Comme nous l'avons vu, notre objectif est de construire un modèle de mélange qui ne nous oblige pas à spécifier le nombre de k clusters / composants depuis le début. Après présentant différentes représentations des processus de Dirichlet, il est maintenant temps d'utiliser réellement les DP pour construire un modèle de mélange infini qui nous permet d'effectuer des regroupements. L'objectif de cet article est de définir les modèles de mélange de processus Dirichlet et de discuter de l'utilisation du processus de restaurant chinois et de l'échantillonnage de Gibbs. Si vous n'avez pas lu les articles précédents, il est fortement recommandé de le faire car le sujet est un peu théorique et nécessite une bonne compréhension de la construction du modèle.

Mise à jour: le Datumbox Machine Learning Framework est désormais open-source et gratuit pour download. Consultez le package com.datumbox.framework.machinelearning.clustering pour voir l'implémentation de Dirichlet Process Mixture Models en Java.

1. Définition du modèle de mélange du procédé Dirichlet

L'utilisation des processus de Dirichlet nous permet d'avoir un modèle de mélange avec des composants infinis qui peut être pensé comme prenant la limite du modèle fini pour k à l'infini. Supposons que nous avons le modèle suivant:

Équation 1: modèle de mélange de processus de Dirichlet

Où G est défini comme ainsi que utilisé comme une courte notation pour qui est une fonction delta qui prend 1 si et 0 ailleurs. Le θ_i sont les paramètres de cluster qui sont échantillonnés à partir de G. La distribution générative F est configurée par les paramètres de cluster θ_i et est utilisé pour générer x_i observations. Enfin, nous pouvons définir une distribution de densité qui est notre distribution de mélange (mélange infini dénombrable) avec des proportions de mélange et mélange de composants .

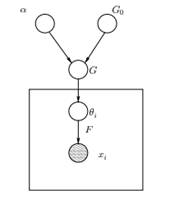
Figure 1: Modèle graphique du modèle de mélange du procédé Dirichlet

Ci-dessus, nous pouvons voir le modèle graphique équivalent du DPMM. Le G₀ est la distribution de base de DP et elle est généralement choisie pour être conjuguée avant notre distribution générative F afin de faciliter les calculs et d'utiliser les propriétés mathématiques attrayantes. L'α est l'hyperparamètre scalaire du processus de Dirichlet et affecte le nombre de clusters que nous obtiendrons. Plus la valeur de α est élevée, plus les grappes sont nombreuses; plus α est petit, moins il y a de grappes. Notons que la valeur de α exprime la force de croire en G₀. Une valeur élevée indique que la plupart des échantillons seront distincts et auront des valeurs concentrées sur G₀. Le G est une distribution aléatoire sur Θ l'espace des paramètres échantillonné à partir du DP qui attribue des probabilités aux paramètres. Le θ_i est un vecteur de paramètres qui est tiré de la distribution G et contient les paramètres du cluster, la distribution F est paramétrée par θ_i et x_i est le point de données généré par la distribution générative F.

Il est important de noter que le θ_i sont des éléments de l'espace des paramètres Θ et ils «configurent» nos clusters. Ils peuvent également être considérés comme des variables latentes sur x_i qui nous indiquent à partir de quel composant / cluster le x_i vient et quels sont les paramètres de ce composant. Ainsi pour chaque x_i que nous observons, nous dessinons un θ_i de la distribution G. A chaque tirage, la distribution change en fonction des sélections précédentes. Comme nous l'avons vu dans le schéma de l'urne Blackwell-MacQueen, la distribution G peut être intégrée et nos futures sélections de θ_i ne dépendent que de G₀: . L'estimation des paramètres θi à partir de la formule précédente n'est pas toujours réalisable car de nombreuses implémentations (telles que Chinese Restaurant Process) impliquent l'énumération via augmentation exponentielle des composants k. Ainsi, des méthodes de calcul approximatives sont utilisées telles que l'échantillonnage de Gibbs. Enfin, notons que même si les k clusters sont infinis, le nombre de clusters actifs est . Ainsi le θ_i va se répéter et présenter un effet de clustering.

2. Utilisation du processus de restaurant chinois pour définir un modèle de mélange infini

Le modèle défini dans le segment précédent est mathématiquement solide, néanmoins il présente un inconvénient majeur: pour chaque nouveau x_i que nous observons, nous devons échantillonner un nouveau θ_i en tenant compte des valeurs précédentes de θ. Le problème est que, dans de nombreux cas, l'échantillonnage de ces paramètres peut être une tâche difficile et coûteuse en calcul.

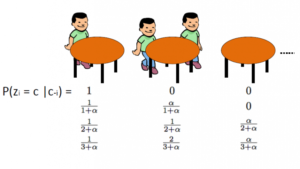
Une approche alternative consiste à utiliser le Chinese Restaurant Process pour modéliser les variables latentes z_i des affectations de cluster. De cette façon, au lieu d'utiliser θ_i pour désigner à la fois les paramètres du cluster et les affectations du cluster, nous utilisons la variable latente z_i pour indiquer l'ID du cluster, puis utilisez cette valeur pour affecter les paramètres du cluster. Par conséquent, nous n'avons plus besoin d'échantillonner a θ chaque fois que nous obtenons une nouvelle observation, mais à la place, nous obtenons l'affectation des grappes en échantillonnant z_i du CRP. Avec ce schéma, un nouveau θ n'est échantillonné que lorsque nous devons créer un nouveau cluster. Ci-dessous, nous présentons le modèle de cette approche:

Équation 2: modèle de mélange avec CRP

Ce qui précède est un modèle génératif qui décrit comment les données x_i et les clusters sont générés. Pour effectuer l'analyse de cluster, nous devons utiliser les observations x_i et estimer les affectations de cluster z_i.

3. Inférence du modèle de mélange et échantillonnage de Gibbs

Malheureusement, étant donné que les processus Dirichlet ne sont pas paramétriques, nous ne peut pas utiliser l'algorithme EM pour estimer les variables latentes qui stockent les affectations de cluster. Afin d'estimer les missions, nous utiliserons le Échantillonnage de Gibbs réduit.

L'échantillonnage de Gibbs réduit est un simple algorithme de chaîne de Markov Monte Carlo (MCMC). Il est rapide et nous permet d'intégrer certaines variables tout en échantillonnant une autre variable. Néanmoins, cet algorithme nous oblige à sélectionner un G₀ qui est un conjugué avant la distribution générative de F afin de pouvoir résoudre analytiquement les équations et pouvoir échantillonner directement à partir de .

Les étapes de l'échantillonnage de Gibbs effondré que nous utiliserons pour estimer les affectations de cluster sont les suivantes:

• Initialiser le z_i affectations de cluster au hasard
• Répéter jusqu'à convergence
• Sélectionner une hache au hasard_i
  
• Gardez l'autre z_j fixe pour chaque j ≠ i:
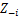
• Attribuer une nouvelle valeur sur z_i en calculant la «probabilité CRP» qui dépend de z_j et x_j de tout j ≠ i:

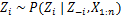
Dans le prochain article, nous nous concentrerons sur la façon d'effectuer une analyse de cluster en utilisant des modèles Dirichlet Process Mixture. Nous définirons deux modèles de mélange de processus Dirichlet différents qui utilisent le processus de restaurant chinois et l'échantillonnage de Gibbs réduit afin d'effectuer un regroupement sur des ensembles de données et des documents continus.