Les mathématiques mystérieuses des tables de billard | Magazine Quanta

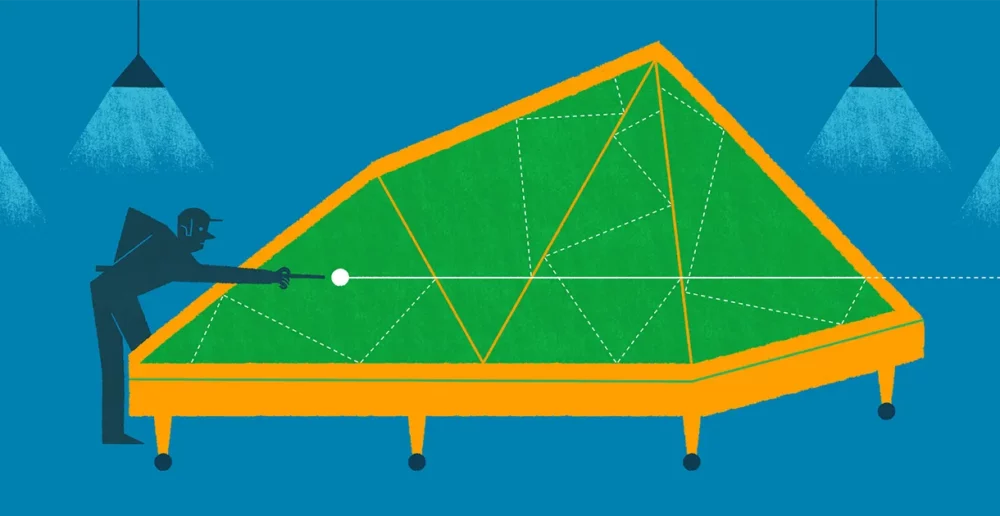
Dans le film de Disney de 1959 Donald au pays des mathématiques, Donald Duck, inspiré par les descriptions du narrateur sur la géométrie du billard, frappe énergiquement la bille blanche, l'envoyant ricocher autour de la table avant qu'il n'atteigne finalement les balles prévues. Donald demande : « Comment aimez-vous cela pour les mathématiques ? »

Étant donné que les tables de billard rectangulaires ont quatre murs se rejoignant à angle droit, les trajectoires de billard comme celle de Donald sont prévisibles et bien comprises, même si elles sont difficiles à réaliser en pratique. Cependant, les mathématiciens chercheurs ne peuvent toujours pas répondre aux questions fondamentales sur les trajectoires possibles des boules de billard sur des tables en forme d'autres polygones (formes à côtés plats). Même les triangles, les polygones les plus simples, recèlent encore des mystères.

Est-il toujours possible de frapper une balle pour qu'elle revienne à son point de départ en se déplaçant dans la même direction, créant ainsi une orbite dite périodique ? Personne ne sait. Pour d'autres formes plus complexes, on ne sait pas s'il est possible de frapper la balle de n'importe quel point de la table vers n'importe quel autre point de la table.

Bien que ces questions semblent s'adapter parfaitement aux limites de la géométrie telle qu'elle est enseignée au lycée, les tentatives pour les résoudre ont obligé certains des plus grands mathématiciens du monde à intégrer des idées issues de domaines disparates, notamment les systèmes dynamiques, la topologie et la géométrie différentielle. Comme pour tout grand problème mathématique, les travaux sur ces problèmes ont créé de nouvelles mathématiques et ont enrichi et fait progresser les connaissances dans ces autres domaines. Pourtant, malgré tous ces efforts et les connaissances apportées par les ordinateurs modernes, ces problèmes apparemment simples résistent obstinément à leur résolution.

Voici ce que les mathématiciens ont appris sur le billard depuis le tir épique de Donald Duck.

Ils supposent généralement que leur boule de billard est un point infiniment petit et sans dimension et qu'elle rebondit sur les murs avec une symétrie parfaite, partant selon le même angle qu'elle arrive, comme on le voit ci-dessous.

Sans friction, la balle se déplace indéfiniment jusqu'à ce qu'elle atteigne un coin qui l'arrête comme une poche. La raison pour laquelle le billard est si difficile à analyser mathématiquement est que deux coups presque identiques atterrissant de chaque côté d’un coin peuvent avoir des trajectoires extrêmement divergentes.

Une méthode clé pour analyser le billard polygonal n'est pas de considérer la balle comme rebondissant sur le bord de la table, mais plutôt d'imaginer que chaque fois que la balle heurte un mur, elle continue de voyager vers une nouvelle copie de la table qui est retournée sur son côté. bord, produisant une image miroir. Ce processus (vu ci-dessous), appelé déroulement du parcours du billard, permet à la balle de continuer selon une trajectoire en ligne droite. En rabattant les tables imaginées sur leurs voisines, vous pourrez récupérer la trajectoire réelle de la balle. Cette astuce mathématique permet de prouver des choses sur la trajectoire qui seraient autrement difficiles à voir.

Par exemple, il peut être utilisé pour montrer pourquoi de simples tableaux rectangulaires ont une infinité de trajectoires périodiques passant par chaque point. Un argument similaire s'applique à n'importe quel rectangle, mais pour des raisons concrètes, imaginez une table deux fois plus large que longue.

Supposons que vous souhaitiez trouver une orbite périodique qui traverse la table n fois dans le sens long et m fois dans le sens court. Puisque chaque image miroir du rectangle correspond à la balle rebondissant sur un mur, pour que la balle revienne à son point de départ en voyageant dans la même direction, sa trajectoire doit traverser la table un nombre pair de fois dans les deux sens. Donc m ainsi que n doit être pair. Disposez une grille de rectangles identiques, chacun étant considéré comme une image miroir de ses voisins. Dessinez un segment de ligne depuis un point de la table d'origine jusqu'au point identique sur une copie n tables éloignées dans le sens long et m tables plus loin dans la direction la plus courte. Ajustez légèrement le point d'origine si le chemin passe par un coin. Voici un exemple où n = 2 et m = 6. Une fois replié, le chemin produit une trajectoire périodique, comme indiqué dans le rectangle vert.

Une inégalité triangulaire

Le billard en triangles, qui n’a pas la belle géométrie rectangulaire des rectangles, est plus compliqué. Comme vous vous en souvenez peut-être en géométrie au lycée, il existe plusieurs types de triangles : les triangles aigus, où les trois angles internes sont inférieurs à 90 degrés ; des triangles rectangles, qui ont un angle de 90 degrés ; et les triangles obtus, dont un angle est supérieur à 90 degrés.

Les tables de billard en forme de triangles aigus et rectangles ont des trajectoires périodiques. Mais personne ne sait s’il en va de même pour les triangles obtus.

Pour trouver une trajectoire périodique dans un triangle aigu, tracez une ligne perpendiculaire allant de chaque sommet au côté opposé, comme on le voit à gauche ci-dessous. Rejoignez les points où se produisent les angles droits pour former un triangle, comme on le voit à droite.

Ce triangle inscrit est une trajectoire de billard périodique appelée orbite de Fagnano, du nom de Giovanni Fagnano, qui montra en 1775 que ce triangle avait le plus petit périmètre de tous les triangles inscrits.

Au début des années 1990, Fred Holt de l'Université de Washington et Grégory Galpérin et ses collaborateurs de l'Université d'État de Moscou indépendamment montré que tout triangle rectangle a des orbites périodiques. Une façon simple de le montrer est de refléter le triangle autour d’une jambe, puis de l’autre, comme indiqué ci-dessous.

Commencez par une trajectoire perpendiculaire à l’hypoténuse (le côté long du triangle). L'hypoténuse et sa seconde réflexion sont parallèles, donc un segment de ligne perpendiculaire les joignant correspond à une trajectoire qui rebondira indéfiniment : la balle quitte l'hypoténuse à angle droit, rebondit sur les deux jambes, revient à l'hypoténuse à droite. angle, puis retrace son itinéraire.

Mais les triangles obtus restent un mystère. Dans leur article de 1992, Galperin et ses collaborateurs ont proposé diverses méthodes permettant de réfléchir des triangles obtus de manière à créer des orbites périodiques, mais ces méthodes ne fonctionnaient que dans certains cas particuliers. Puis, en 2008, Richard Schwartz à l'Université Brown a montré que tous les triangles obtus avec angles de 100 degrés ou moins contiennent une trajectoire périodique. Son approche consistait à décomposer le problème en plusieurs cas et à vérifier chaque cas à l'aide des mathématiques traditionnelles et de l'assistance informatique. En 2018, Jacob Garber, Boyan Marinov, Kenneth Moore et George Tokarsky à l'Université de l'Alberta étendu ce seuil à 112.3 degrés. (Tokarski et Marinov avait passé plus d'une décennie poursuivre cet objectif.)

Un tournant topologique

Une autre approche a été utilisée pour montrer que si tous les angles sont rationnels, c'est-à-dire qu'ils peuvent être exprimés sous forme de fractions, les triangles obtus avec des angles encore plus grands doivent avoir des trajectoires périodiques. Au lieu de simplement copier un polygone sur un plan plat, cette approche mappe des copies de polygones sur des surfaces topologiques, des beignets comportant un ou plusieurs trous.

Si vous réfléchissez un rectangle sur son côté court, puis réfléchissez les deux rectangles sur leur côté le plus long, en créant quatre versions du rectangle d'origine, puis collez le haut et le bas ensemble et la gauche et la droite ensemble, vous aurez fait un beignet, ou tore, comme indiqué ci-dessous. Les trajectoires du billard sur la table correspondent aux trajectoires sur le tore, et vice versa.

Dans un article historique de 1986, Howard Masur a utilisé cette technique pour montrer que toutes les tables polygonales avec des angles rationnels ont des orbites périodiques. Son approche fonctionnait non seulement pour les triangles obtus, mais aussi pour des formes beaucoup plus complexes : des tables irrégulières à 100 côtés, par exemple, ou des polygones dont les murs zigzaguent créant des coins et recoins, ont des orbites périodiques, à condition que les angles soient rationnels.

De manière assez remarquable, l’existence d’une orbite périodique dans un polygone implique l’existence d’une infinité de plusieurs ; décaler légèrement la trajectoire donnera une famille de trajectoires périodiques liées.

Le problème de l'éclairage

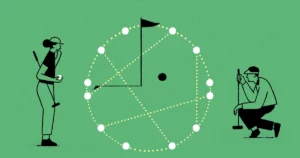
Les formes avec des coins et des recoins soulèvent une question connexe. Plutôt que de s'interroger sur les trajectoires qui reviennent à leur point de départ, ce problème demande si les trajectoires peuvent visiter chaque point d'une table donnée. C'est ce qu'on appelle le problème de l'éclairage, car nous pouvons y réfléchir en imaginant un faisceau laser se réfléchissant sur les murs en miroir entourant la table de billard. Nous demandons si, étant donné deux points sur une table particulière, vous pouvez toujours projeter un laser (idéalisé comme un rayon de lumière infiniment fin) d'un point à l'autre. En d’autres termes, si nous placions une ampoule qui brille dans toutes les directions à la fois, à un moment donné sur la table, éclairerait-elle toute la pièce ?

Il y a eu deux axes de recherche principaux sur le problème : trouver des formes qui ne peuvent pas être éclairées et prouver que de grandes classes de formes peuvent l'être. Alors que trouver des formes étranges qui ne peuvent pas être éclairées peut être réalisé grâce à une application intelligente de mathématiques simples, prouver qu'un grand nombre de formes peuvent être éclairées n'a été possible que grâce à l'utilisation de machines mathématiques lourdes.

En 1958, Roger Penrose, un mathématicien qui a remporté le Prix ​​Nobel de physique 2020, a trouvé une table courbe dans laquelle aucun point d'une région ne pouvait éclairer aucun point d'une autre région. Pendant des décennies, personne n’a pu imaginer un polygone ayant la même propriété. Mais en 1995, Tokarsky a utilisé un simple fait concernant les triangles pour créer un polygone en forme de bloc à 26 côtés avec deux points mutuellement inaccessibles, illustré ci-dessous. Autrement dit, un faisceau laser tiré depuis un point, quelle que soit sa direction, ne peut pas atteindre l'autre point.

L'idée clé utilisée par Tokarsky lors de la construction de sa table spéciale était que si un faisceau laser commence à l'un des angles aigus d'un triangle 45°-45°-90°, il ne pourra jamais revenir vers ce coin.

Sa table déchiquetée est composée de 29 triangles de ce type, disposés pour exploiter intelligemment ce fait. En 2019 Amit Wolecki, alors étudiant diplômé à l'Université de Tel Aviv, a appliqué cette même technique à produire une forme avec 22 côtés (illustré ci-dessous), ce qui, selon lui, était le plus petit nombre possible de côtés pour une forme comportant deux points intérieurs qui ne s'éclairent pas.

Il a été beaucoup plus difficile de prouver des résultats dans l’autre sens. En 2014, Maryam Mirzakhani, mathématicienne à l'Université de Stanford, est devenue la première femme à remporter la médaille Fields, la récompense la plus prestigieuse en mathématiques, pour ses travaux sur les espaces de modules des surfaces de Riemann — une sorte de généralisation des beignets que Masur a utilisée pour montrer que toutes les tables polygonales avec des angles rationnels ont des orbites périodiques. En 2016, Samuel Lelièvre de l'Université Paris-Saclay, Thierry Monteil du Centre National de la Recherche Scientifique et Barak Weiss de l'Université de Tel Aviv a appliqué un certain nombre de résultats de Mirzakhani pour montrer que tout point d'un polygone rationnel éclaire tous les points sauf un nombre fini. Il peut y avoir des points sombres isolés (comme dans les exemples de Tokarsky et Wolecki) mais pas de régions sombres comme dans l'exemple de Penrose, qui a des parois courbes plutôt que droites. Dans Article de Wolecki 2019, il a renforcé ce résultat en prouvant qu'il n'existe qu'un nombre fini de paires de points non éclairables.

Malheureusement, Mirzakhani est mort en 2017 à 40 ans, après une lutte contre le cancer. Son travail semblait très éloigné des coups pièges dans les salles de billard. Et pourtant, l’analyse des trajectoires du billard montre comment même les mathématiques les plus abstraites peuvent être connectées au monde dans lequel nous vivons.