नई सफलता मैट्रिक्स गुणन को आदर्श के करीब लाती है | क्वांटा पत्रिका

कंप्यूटर वैज्ञानिक अत्यधिक मांग वाले समूह हैं। उनके लिए, किसी समस्या का सही उत्तर प्राप्त करना ही पर्याप्त नहीं है - लक्ष्य, लगभग हमेशा, यथासंभव कुशलतापूर्वक उत्तर प्राप्त करना है।

आव्यूहों या संख्याओं की सारणी को गुणा करने का कार्य करें। 1812 में, फ्रांसीसी गणितज्ञ जैक्स फिलिप मैरी बिनेट नियमों का एक बुनियादी सेट लेकर आए, जिसे हम अभी भी छात्रों को पढ़ाते हैं। यह पूरी तरह से अच्छी तरह से काम करता है, लेकिन अन्य गणितज्ञों ने इस प्रक्रिया को सरल और तेज करने के तरीके खोजे हैं। अब का कार्य प्रक्रिया में तेजी लाना मैट्रिक्स गुणन गणित और कंप्यूटर विज्ञान के चौराहे पर स्थित है, जहां शोधकर्ता आज भी इस प्रक्रिया में सुधार कर रहे हैं - हालांकि हाल के दशकों में लाभ काफी मामूली रहा है। 1987 के बाद से, मैट्रिक्स गुणन में संख्यात्मक सुधार "छोटे और ... प्राप्त करना बेहद कठिन" रहे हैं। फ्रांकोइस ले गैल, नागोया विश्वविद्यालय में एक कंप्यूटर वैज्ञानिक।

अब, तीन शोधकर्ताओं - सिंघुआ विश्वविद्यालय के रैन डुआन और रेनफेई झोउ और कैलिफोर्निया विश्वविद्यालय, बर्कले के होंगक्सुन वू - ने इस बारहमासी समस्या पर हमला करने के लिए एक बड़ा कदम आगे बढ़ाया है। उनका नए परिणामले गैल ने कहा, पिछले नवंबर में फाउंडेशन ऑफ कंप्यूटर साइंस कॉन्फ्रेंस में प्रस्तुत किया गया, यह एक अप्रत्याशित नई तकनीक से उपजा है। हालाँकि यह सुधार अपेक्षाकृत छोटा था, ले गैल ने इसे "पिछले अन्य सुधारों की तुलना में वैचारिक रूप से बड़ा" कहा।

यह तकनीक संभावित सुधारों के पहले से अज्ञात और इसलिए अप्रयुक्त स्रोत का खुलासा करती है, और इसका फल पहले ही मिल चुका है: एक दूसरा पेपरजनवरी में प्रकाशित, पहली बार यह दर्शाता है कि मैट्रिक्स गुणन को और भी अधिक कैसे बढ़ाया जा सकता है।

"यह एक बड़ी तकनीकी सफलता है," उन्होंने कहा विलियम कुस्ज़मॉल, हार्वर्ड विश्वविद्यालय में एक सैद्धांतिक कंप्यूटर वैज्ञानिक। "यह मैट्रिक्स गुणन में सबसे बड़ा सुधार है जो हमने एक दशक से अधिक समय में देखा है।"

मैट्रिक्स दर्ज करें

यह एक अस्पष्ट समस्या की तरह लग सकता है, लेकिन मैट्रिक्स गुणन एक मौलिक कम्प्यूटेशनल ऑपरेशन है। यह एल्गोरिदम के एक बड़े हिस्से में शामिल है जिसका उपयोग लोग हर दिन विभिन्न प्रकार के कार्यों के लिए करते हैं, जिसमें तेज कंप्यूटर ग्राफिक्स प्रदर्शित करने से लेकर नेटवर्क सिद्धांत में लॉजिस्टिक समस्याओं को हल करना शामिल है। और गणना के अन्य क्षेत्रों की तरह, गति सर्वोपरि है। यहां तक ​​कि थोड़े से सुधार से भी अंततः समय, कम्प्यूटेशनल शक्ति और धन की महत्वपूर्ण बचत हो सकती है। लेकिन अभी, सिद्धांतकार मुख्य रूप से यह पता लगाने में रुचि रखते हैं कि प्रक्रिया कितनी तेज़ हो सकती है।

दो को गुणा करने का पारंपरिक तरीका n-द्वारा-n मैट्रिक्स - पहले मैट्रिक्स में प्रत्येक पंक्ति से संख्याओं को दूसरे में कॉलम में संख्याओं से गुणा करने की आवश्यकता होती है n³ अलग गुणन. 2-बाय-2 मैट्रिक्स के लिए, इसका मतलब 2 है³ या 8 गुणा.

1969 में, गणितज्ञ वोल्कर स्ट्रैसेन ने एक अधिक जटिल प्रक्रिया का खुलासा किया जो केवल सात गुणक चरणों और 2 अतिरिक्त में 2-ब-18 मैट्रिक्स को गुणा कर सकता था। दो साल बाद, कंप्यूटर वैज्ञानिक शमूएल विनोग्राड ने प्रदर्शित किया कि सात, वास्तव में, 2-बाय-2 मैट्रिक्स के लिए पूर्ण न्यूनतम है।

स्ट्रैसेन ने उसी विचार का उपयोग यह दिखाने के लिए किया कि सब कुछ बड़ा है n-द्वारा-n आव्यूहों को कम से भी गुणा किया जा सकता है n³ कदम। इस रणनीति में एक प्रमुख तत्व में अपघटन नामक एक प्रक्रिया शामिल है - एक बड़े मैट्रिक्स को क्रमिक रूप से छोटे सबमैट्रिस में तोड़ना, जो अंततः 2-बाय-2 या 1-बाय-1 जितना छोटा हो सकता है (ये केवल एकल संख्याएं हैं)।

के अनुसार, एक विशाल सरणी को छोटे टुकड़ों में विभाजित करने का तर्क बहुत सरल है वर्जीनिया वासिलेवस्का विलियम्स, मैसाचुसेट्स इंस्टीट्यूट ऑफ टेक्नोलॉजी में एक कंप्यूटर वैज्ञानिक और नए पेपर में से एक के सह-लेखक। वासिलिव्स्का विलियम्स ने कहा, "एक इंसान के लिए एक बड़े मैट्रिक्स को देखना (मान लीजिए, 100-बाय-100 के क्रम पर) और सर्वोत्तम संभव एल्गोरिदम के बारे में सोचना कठिन है।" यहां तक ​​कि 3-बाय-3 मैट्रिक्स भी अभी तक पूरी तरह से हल नहीं किया जा सका है। "फिर भी, कोई व्यक्ति बड़े मैट्रिक्स के लिए तेज़ एल्गोरिदम प्राप्त करने के लिए पहले से ही छोटे मैट्रिक्स के लिए विकसित किए गए तेज़ एल्गोरिदम का उपयोग कर सकता है।"

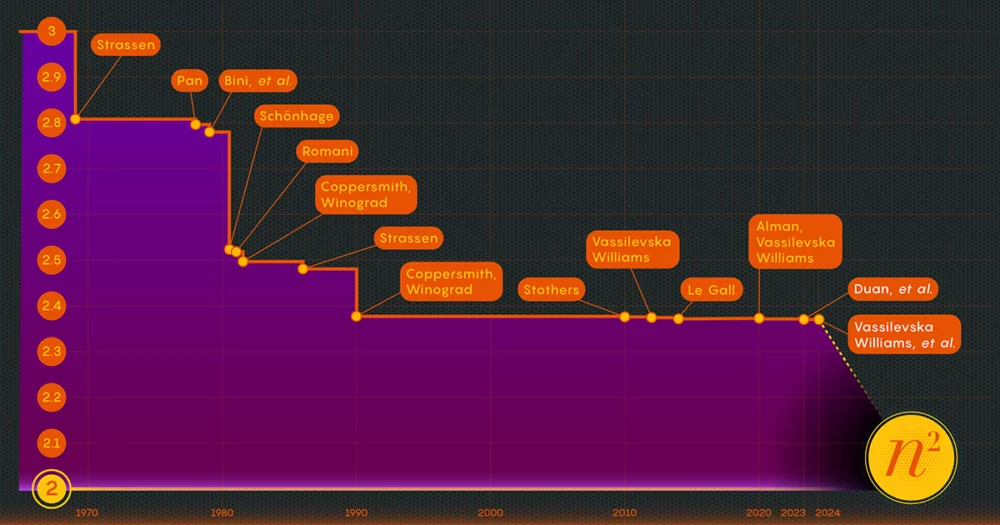
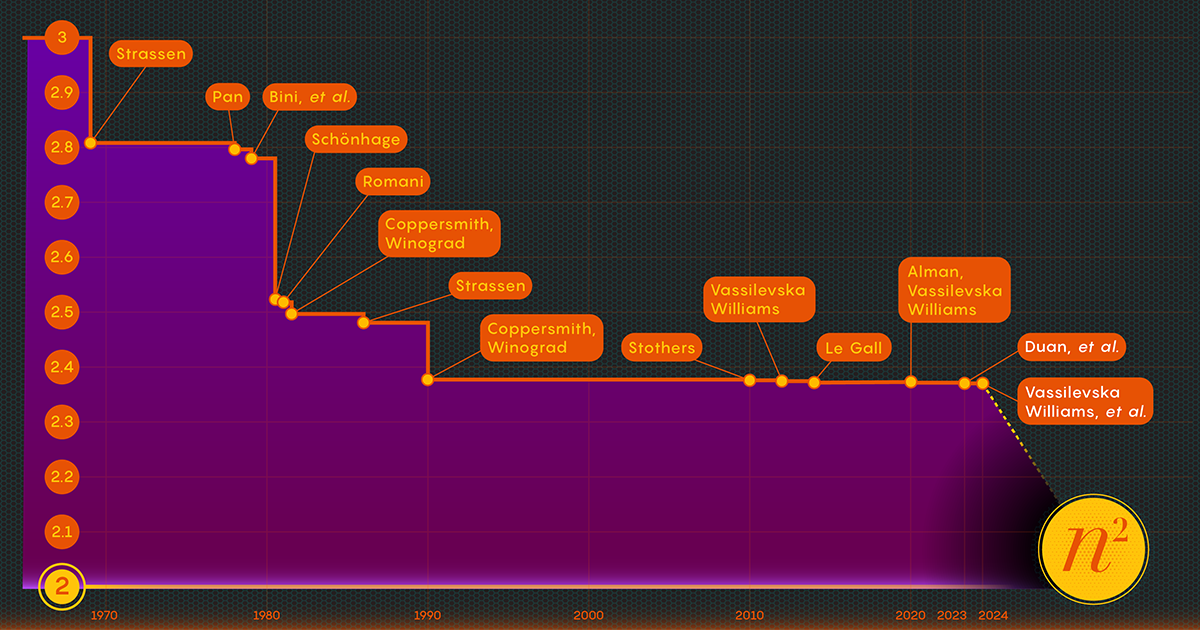
गति की कुंजी, शोधकर्ताओं ने निर्धारित की है, गुणन चरणों की संख्या को कम करना है, उस घातांक को कम करना है n³ (मानक विधि के लिए) जितना वे कर सकते हैं। न्यूनतम संभव मूल्य, n², मूलतः उतना ही समय है जितना उत्तर लिखने में लगता है। कंप्यूटर वैज्ञानिक उस प्रतिपादक को ओमेगा, ω, के रूप में संदर्भित करते हैं n^ω दो को सफलतापूर्वक गुणा करने के लिए आवश्यक न्यूनतम संभव कदम होना n-द्वारा-n मैट्रिक्स के रूप में n बहुत बड़ा हो जाता है. जनवरी 2024 के पेपर के सह-लेखक झोउ ने कहा, "इस काम का उद्देश्य यह देखना है कि आप 2 के कितने करीब आ सकते हैं, और क्या इसे सिद्धांत रूप में हासिल किया जा सकता है।"

एक लेजर फोकस

1986 में, स्ट्रैसेन को एक और बड़ी सफलता मिली जब उन्होंने शुरू की मैट्रिक्स गुणन के लिए लेजर विधि क्या कहलाती है? स्ट्रैसन ने इसका उपयोग ओमेगा के लिए 2.48 का ऊपरी मूल्य स्थापित करने के लिए किया। हालाँकि यह विधि बड़े मैट्रिक्स गुणन में केवल एक कदम है, यह सबसे महत्वपूर्ण में से एक है क्योंकि शोधकर्ताओं ने इसमें सुधार करना जारी रखा है।

एक साल बाद, विनोग्राड और डॉन कॉपरस्मिथ ने एक नया एल्गोरिदम पेश किया जो लेजर विधि को खूबसूरती से पूरक करता था। उपकरणों के इस संयोजन को मैट्रिक्स गुणन को गति देने के लगभग सभी बाद के प्रयासों में शामिल किया गया है।

यहां यह सोचने का एक सरल तरीका है कि ये विभिन्न तत्व एक साथ कैसे फिट होते हैं। आइए दो बड़े मैट्रिक्स, ए और बी से शुरू करें, जिन्हें आप एक साथ गुणा करना चाहते हैं। सबसे पहले, आप उन्हें कई छोटे सबमैट्रिस या ब्लॉक में विघटित करते हैं, जैसा कि उन्हें कभी-कभी कहा जाता है। इसके बाद, आप ब्लॉकों को संभालने और अंततः असेंबल करने के लिए एक प्रकार के निर्देश पुस्तिका के रूप में काम करने के लिए कॉपरस्मिथ और विनोग्राड के एल्गोरिदम का उपयोग कर सकते हैं। "यह मुझे बताता है कि क्या गुणा करना है और क्या जोड़ना है और कौन सी प्रविष्टियाँ कहाँ जाती हैं" उत्पाद मैट्रिक्स सी में, वासिलिव्स्का विलियम्स ने कहा। "यह ए और बी से सी बनाने का एक नुस्खा है।"

हालाँकि, एक समस्या है: कभी-कभी आपको ऐसे ब्लॉक मिल जाते हैं जिनमें प्रविष्टियाँ समान होती हैं। इन्हें उत्पाद में छोड़ना उन प्रविष्टियों को दो बार गिनने के समान होगा, इसलिए किसी बिंदु पर आपको उन दोहराए गए शब्दों से छुटकारा पाना होगा, जिन्हें ओवरलैप्स कहा जाता है। शोधकर्ता ऐसा उन ब्लॉकों को "मार" कर करते हैं जिनमें वे हैं - गणना से उन्हें हटाने के लिए उनके घटकों को शून्य के बराबर सेट करते हैं।

यहीं पर स्ट्रैसेन की लेज़र विधि अंततः चलन में आती है। ले गैल ने कहा, "लेजर विधि आम तौर पर बहुत अच्छी तरह से काम करती है और आम तौर पर ओवरलैप को हटाने के लिए ब्लॉक के सबसेट को मारने का एक अच्छा तरीका ढूंढती है।" लेज़र के ख़त्म हो जाने, या "जल जाने" के बाद, सभी ओवरलैप्स, आप अंतिम उत्पाद मैट्रिक्स, सी का निर्माण कर सकते हैं।

इन विभिन्न तकनीकों को एक साथ रखने से दो आव्यूहों को गुणा करने के लिए एक एल्गोरिदम तैयार होता है, जिसमें समग्र रूप से गुणन की जानबूझकर कंजूस संख्या होती है - कम से कम सिद्धांत में। लेजर विधि व्यावहारिक होने का इरादा नहीं है; यह आव्यूहों को गुणा करने के आदर्श तरीके के बारे में सोचने का एक तरीका मात्र है। झोउ ने कहा, "हम इस विधि को कभी भी [कंप्यूटर पर] नहीं चलाते हैं।" "हम इसका विश्लेषण करते हैं।"

और उस विश्लेषण के कारण एक दशक से भी अधिक समय में ओमेगा में सबसे बड़ा सुधार हुआ।

एक हानि पाई गई है

डुआन, झोउ और वू द्वारा पिछली गर्मियों के पेपर से पता चला कि स्ट्रैसेन की प्रक्रिया में अभी भी काफी तेजी लाई जा सकती है। यह सब उस अवधारणा के कारण था जिसे उन्होंने छिपी हुई हानि कहा था, जो पिछले विश्लेषणों में गहराई से छिपी हुई थी - "अनजाने में बहुत सारे ब्लॉकों को मारने का परिणाम," झोउ ने कहा।

लेजर विधि निपटान के लिए ओवरलैप वाले ब्लॉकों को कचरे के रूप में लेबल करके काम करती है; अन्य ब्लॉकों को योग्य समझा जाएगा और उन्हें बचा लिया जाएगा। हालाँकि, चयन प्रक्रिया कुछ हद तक यादृच्छिक है। कूड़े के रूप में मूल्यांकित ब्लॉक वास्तव में उपयोगी साबित हो सकता है। यह पूरी तरह से आश्चर्य की बात नहीं थी, लेकिन इनमें से कई यादृच्छिक विकल्पों की जांच करके, डुआन की टीम ने निर्धारित किया कि लेजर विधि व्यवस्थित रूप से ब्लॉकों का कम मूल्यांकन कर रही थी: अधिक ब्लॉकों को बचाया जाना चाहिए और कम को बाहर फेंक दिया जाना चाहिए। और, जैसा कि आमतौर पर होता है, कम अपशिष्ट अधिक दक्षता में परिवर्तित होता है।

"ओवरलैप के बिना अधिक ब्लॉक रखने में सक्षम होने से ... एक तेज़ मैट्रिक्स गुणन एल्गोरिदम होता है," ले गैल ने कहा।

इस नुकसान के अस्तित्व को साबित करने के बाद, डुआन की टीम ने लेजर विधि द्वारा ब्लॉक लेबल करने के तरीके को संशोधित किया, जिससे कचरे में काफी कमी आई। परिणामस्वरूप, उन्होंने ओमेगा के लिए लगभग 2.371866 पर एक नई ऊपरी सीमा निर्धारित की - 2.3728596 की पिछली ऊपरी सीमा से एक सुधार, 2020 में सेट किया गया जोश अल्मन और वासिलिव्स्का विलियम्स द्वारा। यह एक मामूली बदलाव की तरह लग सकता है, जिससे सीमा को लगभग 0.001 तक कम किया जा सकता है। लेकिन यह 2010 के बाद से वैज्ञानिकों द्वारा देखा गया सबसे बड़ा सुधार है। तुलनात्मक रूप से वासिलिव्स्का विलियम्स और अल्मन के 2020 के परिणाम में अपने पूर्ववर्ती की तुलना में केवल 0.00001 का सुधार हुआ है।

लेकिन शोधकर्ताओं के लिए जो सबसे रोमांचक बात है वह सिर्फ नया रिकॉर्ड नहीं है - जो लंबे समय तक नहीं चला। यह भी तथ्य है कि अखबार ने सुधार के लिए एक नया रास्ता उजागर किया, जिस पर तब तक पूरी तरह से ध्यान नहीं दिया गया था। ले गैल ने कहा, लगभग चार दशकों से, हर कोई एक ही लेजर विधि पर भरोसा कर रहा है। "तब उन्हें पता चला कि, ठीक है, हम बेहतर कर सकते हैं।"

जनवरी 2024 के पेपर ने इस नए दृष्टिकोण को परिष्कृत किया, जिससे वासिलिव्स्का विलियम्स, झोउ और उनके सह-लेखकों को छिपे हुए नुकसान को और कम करने में सक्षम बनाया गया। इससे ओमेगा की ऊपरी सीमा में अतिरिक्त सुधार हुआ, जिससे यह घटकर 2.371552 रह गई। लेखकों ने आयताकार के लिए गुणन प्रक्रिया को बेहतर बनाने के लिए उसी तकनीक को सामान्यीकृत किया (n-द्वारा-m) मैट्रिसेस - एक प्रक्रिया जिसका ग्राफ़ सिद्धांत, मशीन लर्निंग और अन्य क्षेत्रों में अनुप्रयोग होता है।

इन पंक्तियों के साथ कुछ और प्रगति लगभग निश्चित है, लेकिन इसकी सीमाएँ हैं। 2015 में, ले गैल और दो सहयोगी साबित कि वर्तमान दृष्टिकोण - कॉपरस्मिथ-विनोग्राड रेसिपी के साथ मिलकर लेजर विधि - 2.3078 से नीचे ओमेगा प्राप्त नहीं कर सकती है। कोई और सुधार करने के लिए, ले गैल ने कहा, "आपको कॉपरस्मिथ और विनोग्राड के मूल [दृष्टिकोण] में सुधार करने की आवश्यकता है जो वास्तव में 1987 के बाद से नहीं बदला है". लेकिन अभी तक कोई भी इससे बेहतर तरीका नहीं खोज पाया है। हो सकता है एक भी न हो.

झोउ ने कहा, "ओमेगा में सुधार करना वास्तव में इस समस्या को समझने का हिस्सा है।" “अगर हम समस्या को अच्छी तरह से समझ सकते हैं, तो हम इसके लिए बेहतर एल्गोरिदम डिज़ाइन कर सकते हैं। [और] लोग अभी भी इस सदियों पुरानी समस्या को समझने के शुरुआती चरण में हैं।