1850 में, थॉमस पेनिंगटन किर्कमैन, एक गणितज्ञ, जब वह इंग्लैंड के चर्च में एक पादरी के रूप में अपनी मुख्य जिम्मेदारी को पूरा नहीं कर रहा था, ने अपनी "स्कूली छात्रा की समस्या" का वर्णन किया: "एक स्कूल में पंद्रह युवा महिलाएं लगातार सात दिनों के लिए तीन बार बाहर निकलती हैं: इसकी व्यवस्था करना आवश्यक है उन्हें प्रति दिन दो, ताकि कोई भी दो बार दो बार चल न सके। ”
एक आधुनिक गणितज्ञ के लिए, इस तरह की समस्या की कल्पना एक हाइपरग्राफ के रूप में की जाती है - तीन या अधिक के समूहों में एकत्रित नोड्स का एक सेट। 15 स्कूली छात्राएं नोड हैं, और "तीन बराबर" के प्रत्येक समूह को तीन नोड्स को जोड़ने वाली तीन पंक्तियों या किनारों के साथ एक त्रिभुज के रूप में माना जा सकता है।
किर्कमैन की समस्या अनिवार्य रूप से पूछती है कि क्या इन त्रिभुजों की कोई व्यवस्था है जो सभी स्कूली छात्राओं को एक दूसरे से जोड़ती है, लेकिन अतिरिक्त प्रतिबंध के साथ कि कोई भी दो त्रिकोण एक किनारे को साझा नहीं करते हैं। एज-शेयरिंग का अर्थ होगा कि दो स्कूली छात्राओं को एक से अधिक बार एक साथ चलना होगा। इस प्रतिबंध का मतलब है कि प्रत्येक लड़की एक सप्ताह के लिए हर दिन दो नए दोस्तों के साथ घूमती है, ताकि हर संभव जोड़ी एक बार एक साथ मिल सके।
इस समस्या और इसके जैसे अन्य लोगों ने लगभग दो शताब्दियों तक गणितज्ञों को भ्रमित किया है जब से किर्कमैन ने अपना प्रश्न रखा था। 1973 में, महान गणितज्ञ पॉल एर्डोस ने इसी तरह की एक तस्वीर पेश की थी। उन्होंने पूछा कि क्या दो असंगत गुणों के साथ हाइपरग्राफ बनाना संभव है। सबसे पहले, प्रत्येक जोड़ी नोड्स को बिल्कुल एक त्रिकोण से जोड़ा जाना चाहिए, जैसा कि स्कूली छात्राओं के साथ होता है। यह गुण त्रिभुज के साथ ग्राफ को घना बनाता है। दूसरी आवश्यकता त्रिभुजों को बहुत सटीक तरीके से फैलाने के लिए बाध्य करती है। (विशेष रूप से, यह आवश्यक है कि त्रिभुजों के किसी भी छोटे समूह के लिए, त्रिभुजों की तुलना में कम से कम तीन अधिक नोड हों।) "आपके पास यह थोड़ा विरोधाभासी व्यवहार है जहाँ आपके पास एक सघन समग्र वस्तु है जिसमें कोई घना भाग नहीं है," ने कहा डेविड कोनलोन, कैलिफोर्निया प्रौद्योगिकी संस्थान में गणितज्ञ।
इस जनवरी में एक जटिल 50-पृष्ठ प्रमाण, चार गणितज्ञों ने साबित किया कि जब तक आपके पास पर्याप्त नोड हैं, तब तक ऐसा हाइपरग्राफ बनाना हमेशा संभव है। "जिस तकनीकीता से [वे] गुजरे, बस इसे पाने के लिए, यह आश्चर्यजनक था," ने कहा एलन लो, बर्मिंघम विश्वविद्यालय में गणितज्ञ। कॉनलन ने सहमति व्यक्त की: "यह वास्तव में प्रभावशाली काम है।"
अनुसंधान दल ने एक ऐसी प्रणाली का निर्माण किया जो एर्डोस की शैतानी आवश्यकताओं को पूरा करती है, त्रिकोण चुनने के लिए एक यादृच्छिक प्रक्रिया के साथ शुरू करके और उनकी आवश्यकताओं के अनुरूप अत्यधिक देखभाल के साथ इसे इंजीनियरिंग करती है। "सबूत में जाने वाले कठिन संशोधनों की संख्या वास्तव में चौंका देने वाली है," कॉनलन ने कहा।
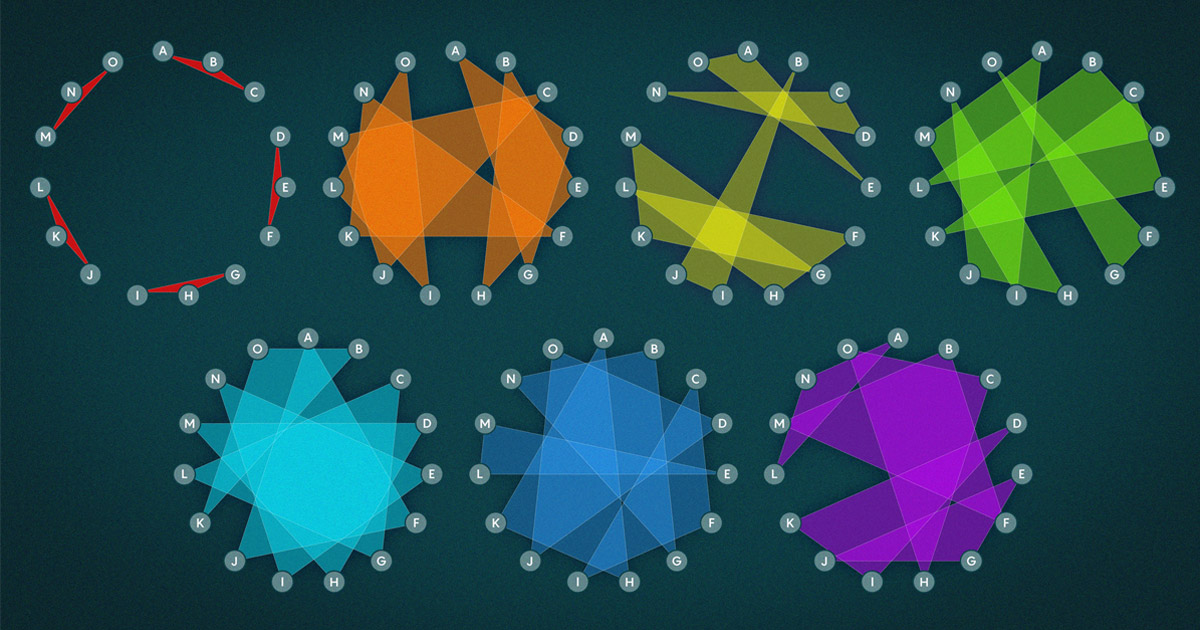
उनकी रणनीति अलग-अलग त्रिकोणों से हाइपरग्राफ को सावधानीपूर्वक बनाने की थी। उदाहरण के लिए, हमारी 15 स्कूली छात्राओं की कल्पना कीजिए। प्रत्येक जोड़ी के बीच एक रेखा खींचें।
यहाँ लक्ष्य इन पंक्तियों के शीर्ष पर त्रिभुजों का पता लगाना है ताकि त्रिभुज दो आवश्यकताओं को पूरा करें: पहला, कोई भी दो त्रिभुज एक किनारे को साझा नहीं करते हैं। (इस आवश्यकता को पूरा करने वाले सिस्टम को स्टीनर ट्रिपल सिस्टम कहा जाता है।) और दूसरा, सुनिश्चित करें कि त्रिकोण का प्रत्येक छोटा सबसेट पर्याप्त रूप से बड़ी संख्या में नोड्स का उपयोग करता है।
जिस तरह से शोधकर्ताओं ने यह किया वह शायद एक सादृश्य के साथ सबसे अच्छी तरह से समझा जा सकता है।
कहें कि किनारों से त्रिकोण बनाने के बजाय, आप लेगो ईंटों से घर बना रहे हैं। आपके द्वारा बनाई गई पहली कुछ इमारतें संरचनात्मक सुदृढीकरण और विस्तृत अलंकरण के साथ असाधारण हैं। एक बार जब आप ये कर लें, तो उन्हें एक तरफ रख दें। वे एक "अवशोषक" के रूप में काम करेंगे - एक प्रकार का संरचित भंडार।
अब अपनी बची हुई ईंटों से इमारतें बनाना शुरू करें, बिना ज्यादा योजना के आगे बढ़ें। जब लेगो की आपूर्ति कम हो जाती है, तो आप अपने आप को कुछ आवारा ईंटों, या घरों के साथ पा सकते हैं जो संरचनात्मक रूप से अस्वस्थ हैं। लेकिन चूंकि अवशोषक इमारतें इतनी अधिक और प्रबलित होती हैं, आप कुछ ईंटों को इधर-उधर तोड़ सकते हैं और तबाही मचाए बिना उनका उपयोग कर सकते हैं।
स्टेनर ट्रिपल सिस्टम के मामले में, आप त्रिकोण बनाने की कोशिश कर रहे हैं। आपका अवशोषक, इस मामले में, किनारों का सावधानीपूर्वक चुना गया संग्रह है। यदि आप अपने आप को शेष प्रणाली को त्रिकोणों में क्रमबद्ध करने में असमर्थ पाते हैं, तो आप कुछ किनारों का उपयोग कर सकते हैं जो अवशोषक में ले जाते हैं। फिर, जब आप ऐसा कर लेते हैं, तो आप अवशोषक को ही त्रिभुजों में तोड़ देते हैं।
अवशोषण हमेशा काम नहीं करता है। लेकिन गणितज्ञों ने इस प्रक्रिया के साथ छेड़छाड़ की है, बाधाओं को दूर करने के नए तरीके खोजे हैं। उदाहरण के लिए, एक शक्तिशाली संस्करण जिसे पुनरावृत्त अवशोषण कहा जाता है, किनारों को सेट के नेस्टेड अनुक्रम में विभाजित करता है, ताकि प्रत्येक अगले सबसे बड़े के लिए अवशोषक के रूप में कार्य करे।
"पिछले एक दशक में या तो बड़े पैमाने पर सुधार हुए हैं," कॉनलन ने कहा। "यह एक कला रूप है, लेकिन उन्होंने वास्तव में इसे इस बिंदु पर उच्च कला के स्तर तक ले जाया है।"
एर्डोस की समस्या पुनरावृत्त अवशोषण के साथ भी मुश्किल थी। "यह बहुत जल्दी स्पष्ट हो गया कि इस समस्या का समाधान क्यों नहीं किया गया," कहा मेहताब साहनी, इसे हल करने वाले चार शोधकर्ताओं में से एक, साथ में अश्विन साहू, जो साहनी के साथ मैसाचुसेट्स इंस्टीट्यूट ऑफ टेक्नोलॉजी में स्नातक छात्र हैं; माइकल सिम्किन, हार्वर्ड विश्वविद्यालय में गणितीय विज्ञान और अनुप्रयोगों के केंद्र में पोस्टडॉक्टरल फेलो; तथा मैथ्यू क्वान, विज्ञान और प्रौद्योगिकी संस्थान ऑस्ट्रिया में गणितज्ञ। "बहुत दिलचस्प, बहुत कठिन तकनीकी कार्य थे।"
उदाहरण के लिए, पुनरावृत्त अवशोषण के अन्य अनुप्रयोगों में, एक बार जब आप एक सेट को कवर करना समाप्त कर लेते हैं - या तो त्रिकोण के साथ, स्टीनर ट्रिपल सिस्टम के लिए, या अन्य समस्याओं के लिए अन्य संरचनाओं के साथ - आप इसे निपटाए जाने पर विचार कर सकते हैं और इसके बारे में भूल सकते हैं। हालांकि, एर्दो की स्थितियों ने चार गणितज्ञों को ऐसा करने से रोक दिया। त्रिभुजों का एक समस्याग्रस्त समूह आसानी से कई अवशोषक सेटों से नोड्स को शामिल कर सकता है।
साहनी ने कहा, "एक त्रिकोण जिसे आपने 500 कदम पहले चुना था, आपको किसी तरह यह याद रखना होगा कि उसके बारे में कैसे सोचना है।"
अंततः चारों को यह पता चला कि यदि वे अपने त्रिभुजों को सावधानी से चुनते हैं, तो वे हर छोटी चीज़ पर नज़र रखने की आवश्यकता को दरकिनार कर सकते हैं। साहनी ने कहा, "यह करना बेहतर है कि 100 त्रिकोणों के किसी भी छोटे सेट के बारे में सोचें और गारंटी दें कि त्रिकोण का सेट सही संभावना के साथ चुना गया है।"
नए पेपर के लेखक आशावादी हैं कि उनकी तकनीक को इस एक समस्या से आगे बढ़ाया जा सकता है। उनके पास है पहले ही अपनी रणनीति लागू कर चुके हैं के बारे में एक समस्या के लिए लैटिन वर्ग, जो एक सुडोकू पहेली के सरलीकरण की तरह हैं।
इसके अलावा, ऐसे कई सवाल हैं जो अंततः अवशोषण के तरीकों को जन्म दे सकते हैं, क्वान ने कहा। "कॉम्बिनेटरिक्स में बहुत सारी समस्याएं हैं, विशेष रूप से डिजाइन सिद्धांत में, जहां यादृच्छिक प्रक्रियाएं वास्तव में एक शक्तिशाली उपकरण हैं।" ऐसी ही एक समस्या, रायसर-ब्रुअलडी-स्टीन अनुमान, लैटिन वर्गों के बारे में भी है और 1960 के दशक से एक समाधान की प्रतीक्षा कर रहा है।
हालांकि अवशोषण को उस समस्या को कम करने से पहले और विकास की आवश्यकता हो सकती है, 30 पहले इसकी स्थापना के बाद से यह एक लंबा सफर तय कर चुका है, ने कहा माया स्टीन, चिली विश्वविद्यालय में गणितीय मॉडलिंग केंद्र के उप निदेशक। "यह कुछ ऐसा है जो वास्तव में यह देखना बहुत अच्छा है कि ये तरीके कैसे विकसित होते हैं।"