1आईसीएफओ-इंस्टीट्यूट डी सिएन्सी फोटोनिक्स, द बार्सिलोना इंस्टीट्यूट ऑफ साइंस एंड टेक्नोलॉजी, 08860 कास्टेलडेफेल्स, स्पेन
2सीएफआईएस-सेंटर डे फॉर्मासिओ इंटरडिसिप्लिनरिया सुपीरियर, यूपीसी-यूनिवर्सिटैट पोलिटेक्निका डी कैटालुन्या, 08028 बार्सिलोना, स्पेन
3यूनिवर्सिटी ग्रेनोबल एल्प्स, सीएनआरएस, ग्रेनोबल आईएनपी, इंस्टिट्यूट नील, 38000 ग्रेनोबल, फ़्रांस
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 बार्सिलोना, स्पेन
इस पेपर को दिलचस्प खोजें या चर्चा करना चाहते हैं? Scate या SciRate पर एक टिप्पणी छोड़ दें.
सार
पारस्परिक रूप से निष्पक्ष आधार क्वांटम सूचना सिद्धांत में माप के अत्यधिक उपयोगी जोड़े के अनुरूप हैं। सबसे छोटे समग्र आयाम, छह में, यह ज्ञात है कि तीन और सात के बीच परस्पर निष्पक्ष आधार मौजूद हैं, दशकों पुराने अनुमान के साथ, जिसे ज़ौनेर के अनुमान के रूप में जाना जाता है, जिसमें कहा गया है कि अधिकतम तीन मौजूद हैं। यहां हम पूर्णांक $n,d ge 2$ के प्रत्येक जोड़े के लिए बेल असमानताओं के निर्माण के माध्यम से ज़ुनेर के अनुमान को संख्यात्मक रूप से निपटाते हैं, जिसका आयाम $d$ में अधिकतम उल्लंघन किया जा सकता है यदि और केवल यदि $n$ MUB उस आयाम में मौजूद हैं। इसलिए हम ज़ुनेर के अनुमान को एक अनुकूलन समस्या में बदल देते हैं, जिसे हम तीन संख्यात्मक तरीकों के माध्यम से संबोधित करते हैं: सी-सॉ अनुकूलन, गैर-रेखीय अर्धनिश्चित प्रोग्रामिंग और मोंटे कार्लो तकनीक। सभी तीन विधियाँ कम आयामों में ज्ञात मामलों की सही पहचान करती हैं और सभी सुझाव देते हैं कि आयाम छह में चार पारस्परिक रूप से निष्पक्ष आधार मौजूद नहीं हैं, सभी समान आधार ढूंढते हैं जो संबंधित बेल असमानता को संख्यात्मक रूप से अनुकूलित करते हैं। इसके अलावा, ये संख्यात्मक अनुकूलक आयाम छह में "चार सबसे दूर के आधारों" के साथ मेल खाते प्रतीत होते हैं, जो [पी में दूरी माप को संख्यात्मक रूप से अनुकूलित करने के माध्यम से पाए जाते हैं। रेनाल, एक्स. लू, बी.-जी. एंगलर्ट, {भौतिकी. रेव. ए}, {83} 062303 (2011)]। अंत में, मोंटे कार्लो परिणाम बताते हैं कि आयाम दस में अधिकतम तीन एमयूबी मौजूद हैं।
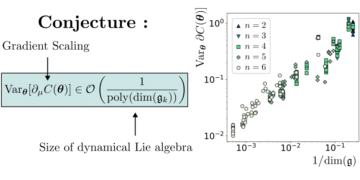
विशेष छवि: हमारी बेल असमानताओं के मान के बीच सापेक्ष अंतर यह मानते हुए कि n MUB आयाम d में मौजूद हैं और हमारे संख्यात्मक तरीकों द्वारा पाया गया मान। शून्य मानों का अर्थ है कि विधियों को आयाम d में n MUB मिले, जबकि गैर-शून्य मानों का अर्थ है कि विधियों को आयाम d में n MUB नहीं मिले। सभी ज्ञात मामले (आयाम दो से पांच और आयाम छह दो और तीन एमयूबी के साथ) संख्याओं द्वारा सही ढंग से पहचाने जाते हैं। आयाम छह में, कोई भी विधि चार एमयूबी नहीं ढूंढती है, और सभी विधियां चार आधारों के एक ही सेट में परिवर्तित हो जाती हैं।
लोकप्रिय सारांश
उनके व्यापक उपयोग के बावजूद, एमयूबी की संरचना के संबंध में अभी भी खुले प्रश्न बने हुए हैं। सबसे प्रमुख रूप से, माप की अधिकतम संख्या जो जोड़ीदार निष्पक्ष है ("एमयूबी की संख्या") अज्ञात है यदि क्वांटम प्रणाली का आयाम एक समग्र संख्या है। विशेष रूप से, आयाम छह में हम केवल यह जानते हैं कि एमयूबी की संख्या तीन और सात के बीच है। ज़ुनेर का एक लंबे समय से खुला अनुमान है, जिसमें कहा गया है कि आयाम छह में तीन से अधिक एमयूबी मौजूद नहीं हैं। यह दशकों पुराना अनुमान कुछ संख्यात्मक साक्ष्यों द्वारा समर्थित है, लेकिन आज तक इसका कोई प्रमाण मौजूद नहीं है।
इस कार्य में हम बेल गैर-इलाके के माध्यम से ज़ुनेर के अनुमान से निपटते हैं। बेल गैर-स्थानीयता दो प्रयोगकर्ताओं से संबंधित है जिन्हें संवाद करने की अनुमति नहीं है, लेकिन शास्त्रीय यादृच्छिकता या साझा क्वांटम स्थिति के रूप में कुछ सहसंबंध साझा कर सकते हैं। यह दिखाया गया है कि क्वांटम संसाधनों को साझा करने से प्रायोगिक डेटा प्राप्त हो सकता है जिसे शास्त्रीय भौतिकी (अधिक सटीक रूप से, तथाकथित स्थानीय छिपे हुए चर मॉडल द्वारा) द्वारा समझाया नहीं जा सकता है। इसे बेल्स प्रमेय के रूप में जाना जाता है, और इसे पिछले दशक में प्रयोगात्मक रूप से सत्यापित किया गया है। प्रयोगात्मक डेटा की गैर-शास्त्रीयता का साक्ष्य आमतौर पर तथाकथित बेल असमानताओं के माध्यम से किया जाता है, जो प्रयोग में होने वाली माप परिणाम संभावनाओं के कार्य हैं। शास्त्रीय डेटा को बेल असमानताओं को संतुष्ट करना चाहिए, जबकि क्वांटम डेटा उनका उल्लंघन कर सकता है।
हाल ही में, बेल असमानताएँ पाई गई हैं जिनका अधिकतम उल्लंघन तब होता है जब कोई एक पक्ष किसी दिए गए आयाम के MUB मापों की एक जोड़ी को नियोजित करता है। इस कार्य में, हम इन असमानताओं को नई असमानताओं तक विस्तारित करते हैं, जिनका किसी दिए गए आयाम में MUB मापों की चयनित संख्या द्वारा अधिकतम उल्लंघन किया जाता है। इसके अलावा, यदि प्रयोग में आयाम तय किया गया है, तो अधिकतम उल्लंघन तब प्राप्त होता है जब नियोजित माप दिए गए आयाम में एमयूबी की चयनित संख्या के अनुरूप होते हैं। इसलिए, यह तय करना कि क्या किसी दिए गए आयाम में चयनित संख्या में एमयूबी मौजूद हैं, इस निश्चित आयाम में संबंधित बेल असमानता के अधिकतम उल्लंघन को खोजने के बराबर है।
जबकि इस अधिकतम उल्लंघन का पता लगाना आम तौर पर एक कठिन समस्या है, हम एक निश्चित आयाम में हमारी बेल असमानताओं के अधिकतम उल्लंघन को खोजने के प्रयास के रूप में तीन अलग-अलग संख्यात्मक तरीकों का उपयोग करते हैं। इनमें से दो विधियाँ अर्धनिश्चित प्रोग्रामिंग तकनीकों के भिन्न रूप हैं, जबकि तीसरी विधि सांख्यिकीय भौतिकी से प्रेरित है और इसे सिम्युलेटेड एनीलिंग कहा जाता है। हालाँकि ये सभी विधियाँ अनुमानी हैं - अर्थात, इस बात की कोई गारंटी नहीं है कि वे समस्या का सही इष्टतम खोज लेंगे - कोई भी उन्हें उन अनुकूलन समस्याओं पर लागू करके उनके प्रदर्शन का अनुमान लगा सकता है, जिनका इष्टतम ज्ञात है। विशेष रूप से, हम पाते हैं कि तीनों विधियां उन मामलों में एमयूबी मापों की सही ढंग से पहचान करने में सक्षम हैं जहां वे मौजूद हैं। इसके अलावा, ऐसे मामलों में जहां वे अस्तित्व में नहीं हैं, सभी तीन विधियां संख्यात्मक परिशुद्धता तक माप के एक ही सेट में परिवर्तित हो जाती हैं। फिर हम अपने तरीकों को पहले अज्ञात मामले में लागू करते हैं, यानी आयाम छह में चार एमयूबी। कोई भी विधि आयाम छह में चार एमयूबी की पहचान करने में सक्षम नहीं है, लेकिन फिर से वे सभी संख्यात्मक परिशुद्धता तक चार मापों के एक ही सेट में परिवर्तित हो जाते हैं। इसके अलावा, सिम्युलेटेड एनीलिंग तकनीक अगले समग्र आयाम, आयाम दस में चार एमयूबी नहीं ढूंढती है। इसलिए, जबकि हमारी तकनीकों की अनुमानी प्रकृति के कारण कठोर दावे नहीं किए जा सकते हैं, हमारे परिणाम बेल गैर-स्थानीयता के नए परिप्रेक्ष्य से ज़ुनेर के अनुमान का समर्थन करते हैं।
► BibTeX डेटा
► संदर्भ
[1] आईडी इवानोविच. मात्रात्मक अवस्था निर्धारण का ज्यामितीय विवरण। जर्नल ऑफ फिजिक्स ए: गणितीय और सामान्य, 14(12):3241-3245, 1981। doi:10.1088/0305-4470/14/12/019।
https://doi.org/10.1088/0305-4470/14/12/019
[2] जी ब्रासार्ड सीएच बेनेट। क्वांटम क्रिप्टोग्राफी: सार्वजनिक कुंजी वितरण और सिक्का उछालना। कंप्यूटर, सिस्टम और सिग्नल प्रोसेसिंग पर आईईईई अंतर्राष्ट्रीय सम्मेलन की कार्यवाही (आईईईई, 1984), 175:8, 1984। doi:10.1016/j.tcs.2011.08.039।
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] आर्थर के. एकर्ट. बेल के प्रमेय पर आधारित क्वांटम क्रिप्टोग्राफी। भौतिक. रेव. लेट., 67:661-663, 1991. doi:10.1103/फिज़रेवलेट.67.661।
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] डागमार ब्रूस. छह अवस्थाओं के साथ क्वांटम क्रिप्टोग्राफी में इष्टतम श्रवण। भौतिक. रेव. लेट., 81:3018-3021, 1998. doi:10.1103/फिज़रेवलेट.81.3018।
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] आर्मिन तवाकोली, एले हमीदी, ब्रेनो मार्क्स, और मोहम्मद बौरेनेन। एकल $d$-स्तर सिस्टम का उपयोग करके क्वांटम रैंडम एक्सेस कोड। भौतिक. रेव. लेट., 114:170502, 2015. doi:10.1103/फिज़रेवलेट.114.170502।
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] माटे फ़ार्कस और जेड्रज़ेज कनिविस्की। तैयार करने और मापने के परिदृश्य में पारस्परिक रूप से निष्पक्ष आधारों का स्व-परीक्षण। भौतिक. रेव ए, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316।
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] एच. बेचमन-पास्किनुची और एन. गिसिन। बाइनरी माप के साथ क्यूनिट्स के लिए बेल असमानता। क्वांटम जानकारी. कंप्यूट., 3(2):157-164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ १०.२६,४२१ / QIC10.26421-3.2
[8] जेद्रेज कानिविस्की, इवान सुपिक, जोर्डी तुरा, फ्लेवियो बेकरी, एलेक्सिया सालाव्राकोस और रेमिगियस ऑगुसियाक। अधिकतम उलझाव और पारस्परिक रूप से निष्पक्ष आधारों से अधिकतम गैर-स्थानीयता, और दो-क्यूट्रिट क्वांटम सिस्टम का स्व-परीक्षण। क्वांटम, 3:198, 2019। doi:10.22331/q-2019-10-24-198।
https://doi.org/10.22331/q-2019-10-24-198
[9] आर्मिन तवाकोली, माटे फ़ार्कस, डेनिस रॉसेट, जीन-डैनियल बैंकल, और जेड्रज़ेज कनिविस्की। बेल प्रयोगों में पारस्परिक रूप से निष्पक्ष आधार और सममित सूचनात्मक रूप से पूर्ण माप। साइंस एडवांस, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847।
https:////doi.org/10.1126/sciadv.abc3847
[10] थॉमस डर्ट, बर्थोल्ड-जॉर्ज एंगलर्ट, इंगमार बेंग्टसन, और करोल ज़िक्ज़कोव्स्की। परस्पर निष्पक्ष आधार पर. क्वांटम सूचना के अंतर्राष्ट्रीय जर्नल, 08(04):535-640, 2010। doi:10.1142/S0219749910006502।
https: / / doi.org/ 10.1142 / S0219749910006502
[11] विलियम के वूटर्स और ब्रायन डी फील्ड्स। पारस्परिक रूप से निष्पक्ष माप द्वारा इष्टतम स्थिति-निर्धारण। एनल्स ऑफ फिजिक्स, 191(2):363-381, 1989. doi:10.1016/0003-4916(89)90322-9।
https://doi.org/10.1016/0003-4916(89)90322-9
[12] पावेल वोक्जन और थॉमस बेथ। वर्गाकार आयामों में परस्पर निष्पक्ष आधारों का नव निर्माण। क्वांटम जानकारी. कंप्यूट., 5(2):93-101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ १०.२६,४२१ / QIC10.26421-5.2
[13] मिहाली वेनर. पारस्परिक रूप से निष्पक्ष आधारों की अधिकतम संख्या के लिए एक अंतर। प्रोक. आमेर. गणित। समाज., 141:1963-1969, 2013। doi:10.1090/S0002-9939-2013-11487-5।
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] गेरहार्ड ज़ुनेर. क्वांटनडिजाइन: ग्रंडज़्यूज एइनर निचटकोम्यूटेटिवन डिज़ाइनथ्योरी। पीएचडी थीसिस, 1999.
[15] पी. ऑस्कर बॉयकिन, मीरा सीतारम, फाम हु टाईप, और पावेल वोकजन। झूठ बीजगणित के पारस्परिक रूप से निष्पक्ष आधार और ऑर्थोगोनल अपघटन। क्वांटम जानकारी. कंप्यूट., 7(4):371-382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ १०.२६,४२१ / QIC10.26421-7.4
[16] स्टीफ़न ब्रिएर्ली और स्टीफ़न वीगर्ट। आयाम छह में परस्पर निष्पक्ष आधारों का निर्माण। भौतिक. रेव. ए, 79:052316, 2009. doi:10.1103/फिजरेवए.79.052316।
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] फिलिप जैमिंग, माटे माटोलसी, पीटर मोरा, फेरेंक स्ज़ोल्सी, और मिहाली वेनर। एक सामान्यीकृत पाउली समस्या और आयाम 6 में एमयूबी-ट्रिपलेट्स का एक अनंत परिवार। जर्नल ऑफ फिजिक्स ए: गणितीय और सैद्धांतिक, 42(24):245305, मई 2009। doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] गैरी मैककोनेल, हैरी स्पेंसर, और अफ़ाक ताहिर। $mathbb{C}^6$ में ज़ुनेर के MUB अनुमान के पक्ष और विपक्ष में साक्ष्य। 2021. doi:10.48550/arXiv.2103.08703।
https://doi.org/10.48550/arXiv.2103.08703
[19] सैंडर ग्रिबलिंग और स्वेन पोलाक। परस्पर निष्पक्ष आधार: बहुपद अनुकूलन और समरूपता। 2021. doi:10.48550/arXiv.2111.05698.
https://doi.org/10.48550/arXiv.2111.05698
[20] इंगेमार बेंग्टसन, वोज्शिएक ब्रुज़्दा, ओसा एरिक्सन, जान-अके लार्सन, वोज्शिएक ताडेज, और करोल ज़्य्ज़कोव्स्की। क्रम छह के पारस्परिक रूप से निष्पक्ष आधार और हैडामर्ड मैट्रिक्स। गणितीय भौतिकी जर्नल, 48(5):052106, 2007. doi:10.1063/1.2716990।
https: / / doi.org/ 10.1063 / १.१३,९४,२०८
[21] फिलिप रेनाल, ज़िन लू, और बर्थोल्ड-जॉर्ज एंगलर्ट। छह आयामों में परस्पर निष्पक्ष आधार: चार सबसे दूर के आधार। भौतिक. रेव. ए, 83:062303, 2011. doi:10.1103/फिजरेवए.83.062303।
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] एडगर ए. एगुइलर, जैकब जे. बोर्काला, पियोट्र मिरोनोविज़, और मार्सिन पावलोव्स्की। परस्पर निष्पक्ष आधारों और क्वांटम रैंडम एक्सेस कोड के बीच संबंध। भौतिक. रेव. लेट., 121:050501, 2018. doi:10.1103/फिज़रेवलेट.121.050501।
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] निकोलस ब्रूनर, डैनियल कैवलकैंटी, स्टेफ़ानो पिरोनियो, वैलेरियो स्कारानी और स्टेफ़नी वेनर। बेल अलोकतांत्रिकता। रेव। मॉड। भौतिक।, ८६:४१९-४७८, २०१४। doi:१०.११०३/RevModPhys.८६.४१९।
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] मोसेक एपीएस। C++ 9.2.49, 2021 के लिए MOSEK फ़्यूज़न एपीआई। URL: https://docs.mosek.com/9.2/cxxfusion/index.html।
https://docs.mosek.com/9.2/cxxfusion/index.html
[25] हिरोशी यामाशिता, हिरोशी याबे, और कौहेई हरादा। अरैखिक अर्धनिश्चित प्रोग्रामिंग के लिए एक प्रारंभिक-दोहरी आंतरिक बिंदु विधि। गणितीय प्रोग्रामिंग, 135(1):89–121, 2012। doi:10.1007/s10107-011-0449-जेड।
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] स्टीफन बोयड और लिवेन वैंडेनबर्ग। उत्तल अनुकूलन। कैम्ब्रिज यूनिवर्सिटी प्रेस, 2004. डोई: 10.1017 / CBO9780511804441।
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] एस. किर्कपैट्रिक, सीडी गेलैट, और एमपी वेक्ची। सिम्युलेटेड एनीलिंग द्वारा अनुकूलन। विज्ञान, 220(4598):671-680, 1983. doi:10.1126/विज्ञान.220.4598.671।
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] निकोलस मेट्रोपोलिस, एरियाना डब्ल्यू. रोसेनब्लुथ, मार्शल एन. रोसेनब्लुथ, ऑगस्टा एच. टेलर, और एडवर्ड टेलर। तेज़ कंप्यूटिंग मशीनों द्वारा राज्य गणना का समीकरण। द जर्नल ऑफ केमिकल फिजिक्स, 21(6):1087-1092, 1953. doi:10.1063/1.1699114।
https: / / doi.org/ 10.1063 / १.१३,९४,२०८
[29] मिगुएल नवास्कुएस, स्टेफ़ानो पिरोनियो, और एंटोनियो एसिन। क्वांटम सहसंबंधों के सेट को बांधना। भौतिक. रेव. लेट., 98:010401, 2007. doi:10.1103/फिज़रेवलेट.98.010401।
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
द्वारा उद्धृत
यह पत्र क्वांटम में प्रकाशित हुआ है क्रिएटिव कॉमन्स एट्रिब्यूशन 4.0 इंटरनेशनल (CC बाय 4.0) लाइसेंस। कॉपीराइट मूल कॉपीराइट धारकों जैसे लेखकों या उनकी संस्थाओं के पास रहता है।