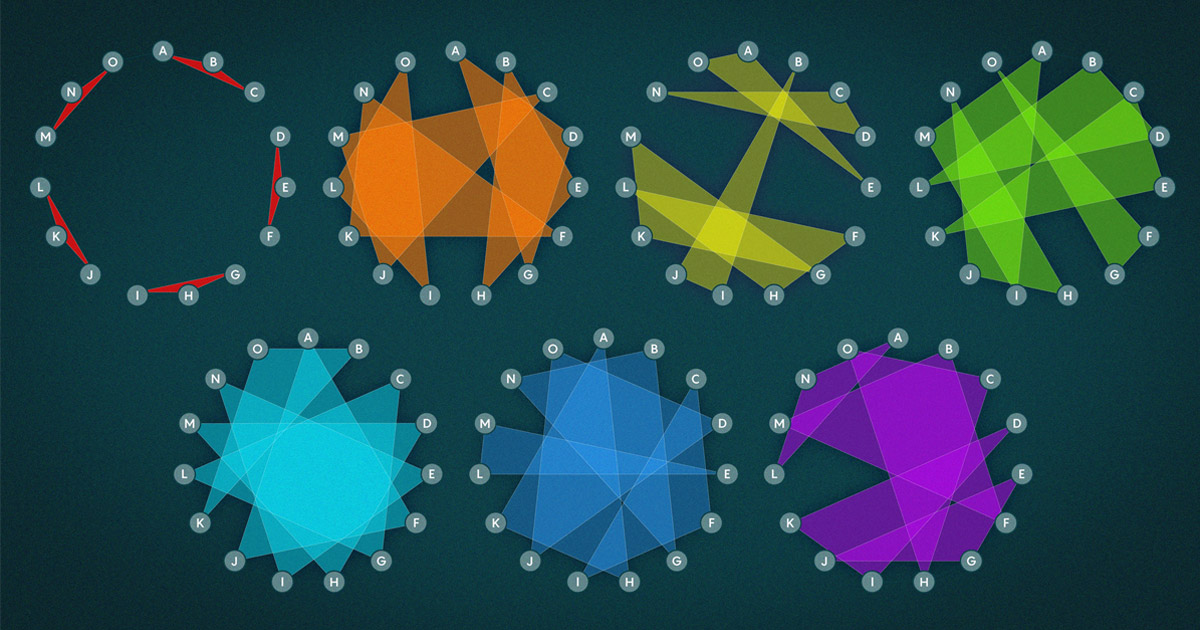
A 1850, Thomas Penynington Kirkman, egy matematikus, amikor nem töltötte be fő feladatait az angliai egyház vikáriusaként, így írta le „iskolásproblémáját”: „Tizenöt fiatal hölgy egy iskolában hét napon át egymás után háromszor sétál ki: gondoskodni kell naponta, hogy ne járjanak kétszer egymás mellett."
Egy modern matematikus számára ez a fajta probléma leginkább hipergráfként képzelhető el – három vagy több csoportba gyűjtött csomópontok halmazaként. A 15 iskoláslány csomópont, és minden „három egymás melletti” csoport egy háromszögnek tekinthető, három vonallal vagy éllel, amelyek három csomópontot kötnek össze.
Kirkman problémája lényegében azt kérdezi, hogy van-e ezeknek a háromszögeknek olyan elrendezése, amely összeköti az összes iskolás lányt egymással, de azzal a további megszorítással, hogy nincs két háromszögnek közös éle. Az élek megosztása azt jelentené, hogy két iskoláslánynak többször kell együtt sétálnia. Ez a korlátozás azt jelenti, hogy minden lány egy héten keresztül minden nap két új baráttal sétál, így minden lehetséges pár pontosan egyszer találkozik.
Ez és a többi hasonló probléma elbűvölte a matematikusokat közel két évszázada azóta, hogy Kirkman feltette a kérdést. 1973-ban a legendás matematikus, Erdős Pál is hasonlót állított fel. Megkérdezte, hogy lehet-e olyan hipergráfot építeni, amely két látszólag összeférhetetlen tulajdonsággal rendelkezik. Először is, minden csomópontpárt pontosan egy háromszöggel kell összekötni, mint az iskolás lányoknál. Ez a tulajdonság háromszögekkel sűrűvé teszi a gráfot. A második követelmény a háromszögek nagyon precíz szétosztását kényszeríti ki. (Konkrétan megköveteli, hogy a háromszögek bármely kis csoportjához legalább hárommal több csomópont legyen, mint ahány háromszög.) „Ez a kissé ellentmondásos viselkedés, amikor egy sűrű, átfogó objektum van, amelynek nincsenek sűrű részei” – mondta. David Conlon, a California Institute of Technology matematikusa.
Idén januárban, bonyolult, 50 oldalas próbanyomat, négy matematikus bebizonyította, hogy mindig lehet ilyen hipergráfot felépíteni, ha van elég csomópont. „Elképesztő volt az a sok technikaiság, amin keresztülmentek, hogy ezt megértsék” – mondta Allan Lo, matematikus a Birminghami Egyetemen. Conlon egyetértett: „Ez egy igazán lenyűgöző alkotás.”
A kutatócsoport egy olyan rendszert épített fel, amely kielégítette Erdős ördögi követelményeit úgy, hogy egy véletlenszerű háromszögválasztási folyamatból indult ki, és rendkívüli gondossággal alakította ki az igényeiknek megfelelően. „A bizonyításba bekerülő bonyolult módosítások száma valóban megdöbbentő” – mondta Conlon.
Stratégiájuk az volt, hogy gondosan építsék fel a hipergráfot az egyes háromszögekből. Képzeljük el például a 15 iskolás lányunkat. Húzzon egy vonalat az egyes párok közé.
A cél itt az, hogy ezeken a vonalakon háromszögeket rajzoljunk ki úgy, hogy a háromszögek két követelménynek eleget tegyenek: Először is, nincs két háromszög közös éle. (Azokat a rendszereket, amelyek teljesítik ezt a követelményt, Steiner hármas rendszereknek nevezzük.) Másodszor pedig ügyeljen arra, hogy a háromszögek minden kis részhalmaza kellően sok csomópontot használjon.
Az, ahogy a kutatók ezt tették, talán a legjobban egy analógiával érthető meg.
Mondd, hogy ahelyett, hogy élekből háromszögeket készítesz, házakat építesz Lego kockákból. Az első néhány épület extravagáns, szerkezeti megerősítésekkel és bonyolult díszítéssel. Ha ezekkel végzett, tedd félre. „Elnyelőként” fognak szolgálni – egyfajta strukturált készletként.
Most kezdjen el épületeket készíteni a megmaradt téglákból, különösebb tervezés nélkül. Amikor a Lego-készleted fogy, előfordulhat, hogy kóbor téglákkal vagy szerkezetileg nem megfelelő otthonokkal találod magad. De mivel az elnyelő épületek annyira túlterheltek és megerősítettek, itt-ott ki lehet szedni néhány téglát, és felhasználni anélkül, hogy katasztrófát okozna.
A Steiner hármas rendszer esetében háromszögeket próbál létrehozni. Az abszorber ebben az esetben egy gondosan kiválasztott élgyűjtemény. Ha úgy találja, hogy nem tudja háromszögekbe rendezni a rendszer többi részét, használhatja az abszorberbe vezető élek egy részét. Aztán, ha ezzel végzett, magát az elnyelőt háromszögekre bontja.
A felszívódás nem mindig működik. A matematikusok azonban bütykölték a folyamatot, és új módszereket találtak az akadályok megkerülésére. Például az iteratív abszorpciónak nevezett erőteljes változat az éleket halmazok egymásba ágyazott sorozatára osztja, így mindegyik a következő legnagyobb elnyelőjeként működik.
„Az elmúlt évtizedben hatalmas fejlődés ment végbe” – mondta Conlon. „Ez valami művészeti forma, de ezen a ponton valóban felvitték a magas művészet szintjére.”
Erdős problémája még az iteratív abszorpcióval is trükkös volt. „Gyorsan világossá vált, hogy miért nem sikerült megoldani ezt a problémát” – mondta Mehtaab Sawhney, egyike annak a négy kutatónak, akik megoldották, valamint Ashwin Sah, aki Sawhney mellett a Massachusetts Institute of Technology végzős hallgatója; Michael Simkin, posztdoktori ösztöndíjas a Harvard Egyetem Matematikai Tudományok és Alkalmazások Központjában; és Matthew Kwan, matematikus az Ausztriai Tudományos és Technológiai Intézetben. "Elég érdekes, elég nehéz technikai feladatok voltak."
Például az iteratív abszorpció más alkalmazásaiban, ha befejezett egy halmaz lefedését – akár háromszögekkel, akár Steiner hármasrendszereknél, akár más struktúrákkal más problémák esetén –, kezeltnek tekintheti, és elfelejtheti. Erdős körülményei azonban megakadályozták a négy matematikust ebben. Egy problémás háromszögcsoport könnyen tartalmazhat csomópontokat több abszorberkészletből.
„Egy háromszög, amelyet 500 lépéssel ezelőtt választottál, valahogy emlékezned kell arra, hogyan kell erről gondolkodni” – mondta Sawhney.
A négyen végül rájöttek, hogy ha gondosan választják meg a háromszögeiket, akkor megkerülhetik, hogy minden apróságot nyomon kell követniük. „Jobb, ha minden kis, 100 háromszögből álló halmazra gondolunk, és garantáljuk, hogy a háromszöghalmazt a megfelelő valószínűséggel választjuk ki” – mondta Sawhney.
Az új cikk szerzői bizakodóak abban, hogy technikájuk ezen az egyetlen problémán túl is kiterjeszthető. Van nekik már alkalmazták stratégiájukat kapcsolatos problémára Latin négyzetek, amelyek olyanok, mint egy sudoku rejtvény leegyszerűsítése.
Ezen túlmenően számos kérdés merülhet fel, amelyek végül engedhetnek az abszorpciós módszereknek, mondta Kwan. "Annyi probléma van a kombinatorikában, különösen a tervezéselméletben, ahol a véletlenszerű folyamatok nagyon hatékony eszközt jelentenek." Az egyik ilyen probléma, a Ryser-Brualdi-Stein sejtés szintén a latin négyzetekre vonatkozik, és az 1960-as évek óta vár megoldásra.
Noha az abszorpció további fejlesztésre szorulhat, mielőtt megoldja ezt a problémát, hosszú utat tett meg 30 évvel ezelőtti kezdete óta. Maya Stein, a Chilei Egyetem Matematikai Modellezési Központjának igazgatóhelyettese. "Nagyon jó látni, hogyan fejlődnek ezek a módszerek."