1ICFO-Institut de Ciencies Fotoniques, Barcelona Tudományos és Technológiai Intézet, 08860 Castelldefels, Spanyolország
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spanyolország
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Franciaország
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spanyolország
Érdekesnek találja ezt a cikket, vagy szeretne megvitatni? Scite vagy hagyjon megjegyzést a SciRate-en.
Absztrakt
A kölcsönösen torzítatlan bázisok a kvantuminformáció-elméletben rendkívül hasznos mérési pároknak felelnek meg. A legkisebb összetett dimenzióban, a hatban, ismert, hogy három és hét közötti, kölcsönösen elfogulatlan bázis létezik, egy évtizedes sejtés, amely Zauner sejtéseként ismert, és azt állítja, hogy legfeljebb három létezik. Itt Zauner sejtését numerikusan kezeljük a Bell-egyenlőtlenségek felépítésével minden $n,d ge 2$ egész számpárra, amelyek maximálisan megsérthetők a $d$ dimenzióban, ha és csak akkor, ha $n$ MUB van ebben a dimenzióban. Ennélfogva Zauner sejtését optimalizálási problémává változtatjuk, amelyet három numerikus módszerrel kezelünk: libikóka optimalizálással, nemlineáris félig meghatározott programozással és Monte Carlo technikákkal. Mindhárom módszer helyesen azonosítja az ismert eseteket alacsony dimenziókban, és mindegyik azt sugallja, hogy a hatodik dimenzióban nem létezik négy kölcsönösen torzítatlan bázis, és mindegyik ugyanazokat az alapokat találja, amelyek numerikusan optimalizálják a megfelelő Bell-egyenlőtlenséget. Ezen túlmenően úgy tűnik, hogy ezek a numerikus optimalizálók egybeesnek a „négy legtávolabbi bázissal” a hatodik dimenzióban, amelyeket egy távolságmérték numerikus optimalizálásával találtunk meg [P. Raynal, X. Lü, B.-G. Englert, {Phys. Rev. A}, { 83} 062303 (2011)]. Végül a Monte Carlo-i eredmények azt sugallják, hogy a tízes dimenzióban legfeljebb három MUB létezik.
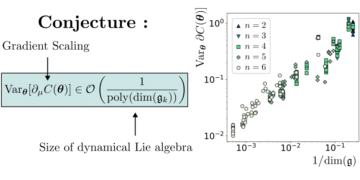
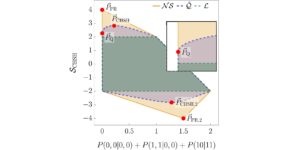
Kiemelt kép: Bell-egyenlőtlenségeink értéke, feltéve, hogy n MUB létezik a d dimenzióban, és a numerikus módszereinkkel talált érték közötti relatív különbség. A nulla értékek azt jelentik, hogy a módszerek n MUB-ot találtak a d dimenzióban, míg a nem nulla értékek azt jelentik, hogy a módszerek nem találtak n MUB-ot a d dimenzióban. Az összes ismert esetet (a kettőtől ötig terjedő dimenzió és a hatodik dimenzió két és három MUB-val) helyesen azonosítja a számok. A hatodik dimenzióban egyik metódus sem talál négy MUB-ot, és az összes metódus ugyanahhoz a négy bázisból álló halmazhoz konvergál.
Népszerű összefoglaló
Széles körű használatuk ellenére továbbra is vannak nyitott kérdések a MUB-ok szerkezetével kapcsolatban. A legszembetűnőbb, hogy a páronként elfogulatlan mérések maximális száma („MUB-ok száma”) nem ismert, ha a kvantumrendszer dimenziója összetett szám. A hatodik dimenzióban csak azt tudjuk, hogy a MUB-ok száma három és hét között van. Egy régóta fennálló nyílt sejtés Zauner sejtése, amely szerint a hatodik dimenzióban legfeljebb három MUB létezik. Ezt a több évtizedes sejtést számos számszerű bizonyíték támasztja alá, de a mai napig nincs bizonyíték.
Ebben a munkában Zauner sejtését Bell nem lokalitásán keresztül kezeljük. A Bell nem lokalitás két kísérletezőt érint, akik nem kommunikálhatnak, de megoszthatnak egymással összefüggéseket a klasszikus véletlenszerűség vagy egy közös kvantumállapot formájában. Kimutatták, hogy a kvantumerőforrások megosztása olyan kísérleti adatokhoz vezethet, amelyek a klasszikus fizikával (pontosabban az úgynevezett lokális rejtett változós modellekkel) nem magyarázhatók. Ezt Bell-tételként ismerik, és az elmúlt évtizedben kísérletileg igazolták. A kísérleti adatok nem klasszikusságának tanúja leggyakrabban az úgynevezett Bell-egyenlőtlenségeken keresztül történik, amelyek a kísérletben előforduló mérési eredmény valószínűségeinek függvényei. A klasszikus adatoknak ki kell elégíteniük a Bell-egyenlőtlenségeket, míg a kvantumadatok megsérthetik azokat.
A közelmúltban olyan Bell-egyenlőtlenségeket találtak, amelyek maximálisan sérülnek, ha az egyik fél egy adott dimenziójú MUB-méréspárt alkalmaz. Ebben a munkában ezeket az egyenlőtlenségeket kiterjesztjük újakra, amelyeket egy adott dimenzióban kiválasztott számú MUB mérés maximálisan megsért. Ezen túlmenően, ha a kísérletben a dimenzió rögzített, akkor a maximális megsértés akkor és csak akkor érhető el, ha az alkalmazott mérések megfelelnek az adott dimenzióban kiválasztott számú MUB-nak. Ezért annak eldöntése, hogy egy kiválasztott számú MUB létezik-e egy adott dimenzióban, megegyezik a megfelelő Bell-egyenlőtlenség maximális megsértésének megállapításával ebben a rögzített dimenzióban.
Noha ennek a maximális megsértésnek a megtalálása általában nehéz probléma, három különböző numerikus módszert alkalmazunk annak érdekében, hogy megtaláljuk Bell-egyenlőtlenségeink maximális sértését egy rögzített dimenzióban. E módszerek közül kettő a félig meghatározott programozási technikák változata, míg a harmadik a statisztikai fizika ihlette, és az úgynevezett szimulált lágyítás. Noha ezek a módszerek mindegyike heurisztikus – vagyis nincs garancia arra, hogy megtalálják a probléma valódi optimumát –, teljesítményüket olyan optimalizálási problémákra is felmérhetjük, amelyek optimuma ismert. Különösen azt találtuk, hogy mindhárom módszer helyesen képes azonosítani a MUB-méréseket azokban az esetekben, amikor ismert, hogy léteznek. Továbbá azokban az esetekben, amelyekről ismert, hogy nem léteznek, mindhárom módszer ugyanahhoz a mérési sorozathoz konvergál a numerikus pontosságig. Ezután alkalmazzuk a módszereinket az első ismeretlen esetre, azaz négy MUB-ra a hatodik dimenzióban. A módszerek egyike sem képes négy MUB-ot azonosítani a hatodik dimenzióban, de mindegyik ugyanahhoz a négy mérésből álló halmazhoz konvergál a numerikus pontosságig. Ezenkívül a szimulált lágyítási technika nem talál négy MUB-ot a következő kompozit dimenzióban, a tízes dimenzióban. Ezért, bár technikáink heurisztikus természete miatt szigorú állítások nem tehetők, eredményeink alátámasztják Zauner sejtését a Bell nem lokalitás új perspektívájából.
► BibTeX adatok
► Referenciák
[1] ID Ivanovic. A kvantális állapot meghatározás geometriai leírása. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kvantum kriptográfia: Nyilvános kulcs elosztása és érmefeldobás. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https:///doi.org/10.1016/j.tcs.2011.08.039
[3] Artur K. Ekert. Kvantum kriptográfia Bell tétele alapján. Phys. Rev. Lett., 67:661–663, 1991. doi: 10.1103/PhysRevLett.67.661.
https:///doi.org/10.1103/PhysRevLett.67.661
[4] Dagmar Bruß. Optimális lehallgatás hat állapotú kvantumkriptográfiában. Phys. Rev. Lett., 81:3018–3021, 1998. doi: 10.1103/PhysRevLett.81.3018.
https:///doi.org/10.1103/PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques és Mohamed Bourennane. Kvantum véletlen hozzáférésű kódok egyetlen $d$ szintű rendszerrel. Phys. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https:///doi.org/10.1103/PhysRevLett.114.170502
[6] Farkas Máté és Jędrzej Kaniewski. Kölcsönösen elfogulatlan alapok önellenőrzése az előkészítés és mérés forgatókönyvében. Phys. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https:///doi.org/10.1103/PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci és N. Gisin. Bell-egyenlőtlenség kvnitekhez bináris mérésekkel. Quantum Info. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https:///doi.org/10.26421/QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos és Remigiusz Augusiak. Maximális nonlokalitás a maximális összefonódásból és kölcsönösen elfogulatlan bázisokból, valamint a kétkvtrites kvantumrendszerek öntesztelése. Quantum, 3:198, 2019. doi: 10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Tavakoli Armin, Farkas Máté, Denis Rosset, Jean-Daniel Bancal és Jędrzej Kaniewski. Kölcsönösen elfogulatlan bázisok és szimmetrikus információs szempontból teljes mérések a Bell-kísérletekben. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson és Karol Życzkowski. Kölcsönösen elfogulatlan alapokon. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https:///doi.org/10.1142/S0219749910006502
[11] William K Wootters és Brian D Fields. Optimális állapotmeghatározás kölcsönösen torzítatlan mérésekkel. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan és Thomas Beth. Kölcsönösen elfogulatlan alapok új konstrukciója négyzetes méretekben. Quantum Info. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https:///doi.org/10.26421/QIC5.2-1
[13] Weiner Mihály. Egy rés a kölcsönösen elfogulatlan bázisok maximális számához. Proc. Amer. Math. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. PhD értekezés, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep és Pawel Wocjan. A Lie-algebrák kölcsönösen torzítatlan bázisai és ortogonális dekompozíciói. Quantum Info. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https:///doi.org/10.26421/QIC7.4-6
[16] Stephen Brierley és Stefan Weigert. Kölcsönösen torzítatlan bázisok megalkotása a hatodik dimenzióban. Phys. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https:///doi.org/10.1103/PhysRevA.79.052316
[17] Philippe Jaming, Matolcsi Máté, Móra Péter, Szöllősi Ferenc, és Weiner Mihály. Egy általánosított Pauli-probléma és a MUB-hármasok végtelen családja a 6-os dimenzióban. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, 2009. május. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer és Afaq Tahir. Bizonyítékok Zauner MUB-sejtése mellett és ellen a $mathbb{C}^6$-ban. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling és Sven Polak. Kölcsönösen torzítatlan bázisok: polinom optimalizálás és szimmetria. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej és Karol Życzkowski. Kölcsönösen elfogulatlan bázisok és hatodrendű Hadamard-mátrixok. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https:///doi.org/10.1063/1.2716990
[21] Philippe Raynal, Xin Lü és Berthold-Georg Englert. Kölcsönösen elfogulatlan bázisok hat dimenzióban: A négy legtávolabbi bázis. Phys. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https:///doi.org/10.1103/PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz és Marcin Pawłowski. Kölcsönösen torzítatlan bázisok és kvantum véletlen hozzáférésű kódok közötti kapcsolatok. Phys. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https:///doi.org/10.1103/PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani és Stephanie Wehner. Bell nem lokalitás. Rev. Mod. Phys., 86:419–478, 2014. doi:10.1103/RevModPhys.86.419.
https:///doi.org/10.1103/RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API for C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe és Kouhei Harada. Egy primál-két belső pont módszer nemlineáris félig meghatározott programozáshoz. Matematikai programozás, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https:///doi.org/10.1007/s10107-011-0449-z
[26] Stephen Boyd és Lieven Vandenberghe. Konvex optimalizálás. Cambridge University Press, 2004. doi: 10.1017/CBO9780511804441.
https:///doi.org/10.1017/CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt és MP Vecchi. Optimalizálás szimulált lágyítással. Science, 220 (4598): 671–680, 1983. doi: 10.1126/tudomány.220.4598.671.
https:///doi.org/10.1126/science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller és Edward Teller. Állapotszámítások egyenlete gyors számítástechnikai gépekkel. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https:///doi.org/10.1063/1.1699114
[29] Miguel Navascués, Stefano Pironio és Antonio Acín. A kvantumkorrelációk halmazának behatárolása. Phys. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https:///doi.org/10.1103/PhysRevLett.98.010401
Idézi
Ez a tanulmány a Quantumban jelent meg Creative Commons Nevezd meg 4.0 International (CC BY 4.0) engedély. A szerzői jog az eredeti szerzői jog tulajdonosainál marad, például a szerzőknél vagy intézményeiknél.