Terobosan Baru Membawa Perkalian Matriks Mendekati Ideal | Majalah Kuanta

Ilmuwan komputer adalah kelompok yang banyak menuntut. Bagi mereka, mendapatkan jawaban yang benar terhadap suatu masalah saja tidak cukup — tujuannya hampir selalu adalah mendapatkan jawaban seefisien mungkin.

Lakukan tindakan mengalikan matriks, atau susunan angka. Pada tahun 1812, ahli matematika Perancis Jacques Philippe Marie Binet menemukan seperangkat aturan dasar yang masih kami ajarkan kepada siswa. Ini berfungsi dengan baik, namun matematikawan lain telah menemukan cara untuk menyederhanakan dan mempercepat prosesnya. Sekarang tugas mempercepat prosesnya Perkalian matriks terletak pada titik temu antara matematika dan ilmu komputer, di mana para peneliti terus menyempurnakan prosesnya hingga saat ini — meskipun dalam beberapa dekade terakhir, kemajuan yang dicapai masih terbilang kecil. Sejak tahun 1987, peningkatan numerik dalam perkalian matriks “kecil dan… sangat sulit diperoleh,” katanya Francois Le Gall, seorang ilmuwan komputer di Universitas Nagoya.

Kini, tiga peneliti – Ran Duan dan Renfei Zhou dari Universitas Tsinghua dan Hongxun Wu dari Universitas California, Berkeley – telah mengambil langkah maju yang besar dalam mengatasi masalah abadi ini. Milik mereka hasil baru, yang dipresentasikan pada November lalu di konferensi Yayasan Ilmu Komputer, berasal dari teknik baru yang tidak terduga, kata Le Gall. Meskipun peningkatannya sendiri relatif kecil, Le Gall menyebutnya “secara konseptual lebih besar dibandingkan perbaikan sebelumnya.”

Teknik ini mengungkap sumber perbaikan potensial yang sebelumnya tidak diketahui dan karenanya belum dimanfaatkan, dan telah membuahkan hasil: Makalah kedua, yang diterbitkan pada bulan Januari, merupakan pengembangan dari penelitian pertama yang menunjukkan bagaimana perkalian matriks dapat ditingkatkan lebih jauh lagi.

“Ini adalah terobosan teknis yang besar,” katanya William Kuszmaul, seorang ilmuwan komputer teoretis di Universitas Harvard. “Ini merupakan peningkatan terbesar dalam perkalian matriks yang pernah kami lihat selama lebih dari satu dekade.”

Masukkan Matriks

Ini mungkin tampak seperti masalah yang tidak jelas, tetapi perkalian matriks adalah operasi komputasi yang mendasar. Ini dimasukkan ke dalam sebagian besar algoritme yang digunakan orang setiap hari untuk berbagai tugas, mulai dari menampilkan grafik komputer yang lebih tajam hingga memecahkan masalah logistik dalam teori jaringan. Dan seperti dalam bidang komputasi lainnya, kecepatan adalah hal yang terpenting. Perbaikan sekecil apa pun pada akhirnya dapat menghemat waktu, tenaga komputasi, dan uang secara signifikan. Namun untuk saat ini, para ahli teori terutama tertarik untuk mengetahui seberapa cepat proses tersebut dapat terjadi.

Cara tradisional mengalikan dua n-oleh-n matriks — dengan mengalikan angka-angka dari setiap baris pada matriks pertama dengan angka-angka pada kolom-kolom pada matriks kedua — memerlukan n³ perkalian terpisah. Untuk matriks 2-kali-2, artinya 2³ atau 8 perkalian.

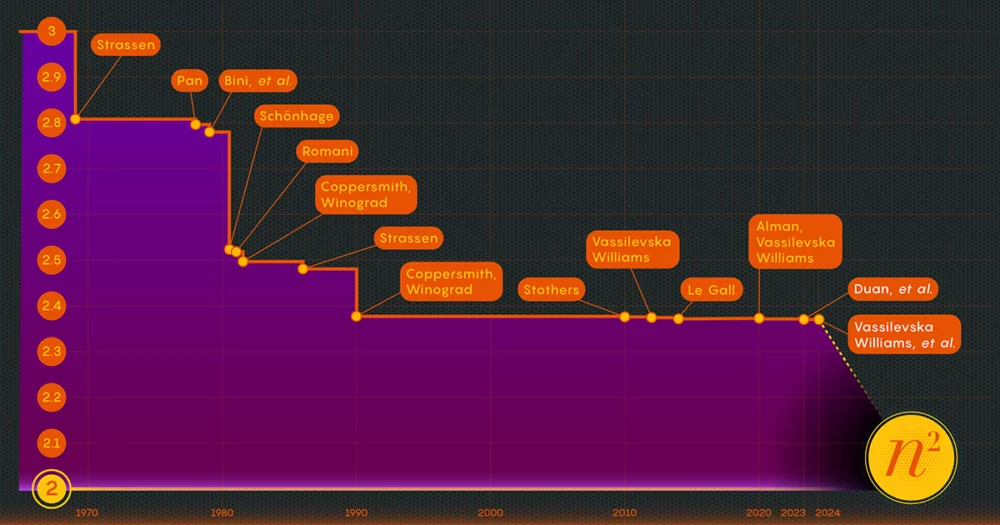
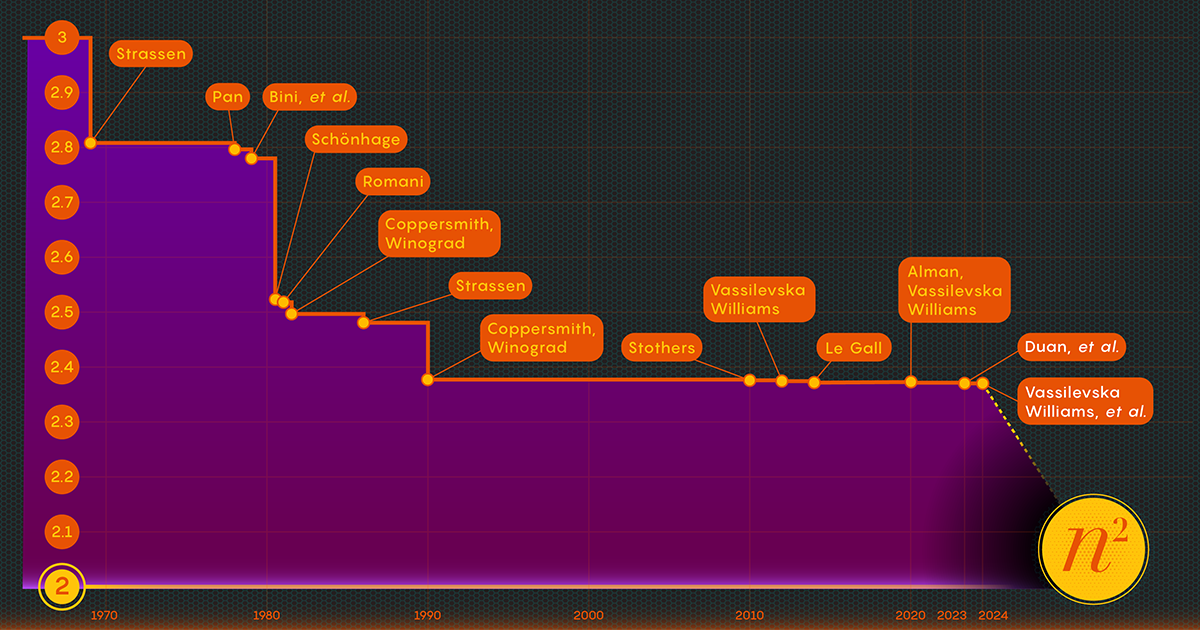
Pada tahun 1969, ahli matematika Volker Strassen mengungkapkan prosedur yang lebih rumit yang dapat mengalikan matriks 2-kali-2 hanya dalam tujuh langkah perkalian dan 18 penjumlahan. Dua tahun kemudian, ilmuwan komputer Shmuel Winograd mendemonstrasikan bahwa tujuh memang merupakan nilai minimum absolut untuk matriks 2-kali-2.

Strassen memanfaatkan gagasan yang sama untuk menunjukkan bahwa semuanya lebih besar n-oleh-n matriks juga dapat dikalikan dalam waktu kurang dari n³ Langkah. Elemen kunci dalam strategi ini melibatkan prosedur yang disebut dekomposisi - memecah matriks besar menjadi submatriks yang lebih kecil, yang mungkin akan menjadi sekecil 2-kali-2 atau bahkan 1-kali-1 (ini hanyalah angka tunggal).

Alasan untuk membagi array raksasa menjadi potongan-potongan kecil cukup sederhana, menurutnya Virginia Vassilevska Williams, seorang ilmuwan komputer di Massachusetts Institute of Technology dan salah satu penulis salah satu makalah baru. “Sulit bagi manusia untuk melihat matriks yang besar (katakanlah, pada urutan 100-kali-100) dan memikirkan algoritma terbaik,” kata Vassilevska Williams. Bahkan matriks 3-kali-3 belum terpecahkan sepenuhnya. “Namun demikian, seseorang dapat menggunakan algoritma cepat yang telah dikembangkan untuk matriks kecil untuk juga mendapatkan algoritma cepat untuk matriks yang lebih besar.”

Kunci kecepatan, menurut para peneliti, adalah mengurangi jumlah langkah perkalian, menurunkan eksponennya n³ (untuk metode standar) sebanyak yang mereka bisa. Nilai serendah mungkin, n², pada dasarnya adalah waktu yang diperlukan untuk menulis jawabannya. Ilmuwan komputer menyebut eksponen tersebut sebagai omega, ω, dengan n^ω menjadi langkah sesedikit mungkin yang diperlukan agar berhasil mengalikan dua n-oleh-n matriks sebagai n tumbuh sangat besar. “Inti dari penelitian ini,” kata Zhou, yang juga ikut menulis makalah pada bulan Januari 2024, “adalah untuk melihat seberapa dekat Anda bisa mencapai angka 2, dan apakah hal tersebut dapat dicapai secara teori.”

Fokus Laser

Pada tahun 1986, Strassen kembali membuat terobosan besar ketika dia diperkenalkan apa yang disebut metode laser untuk perkalian matriks. Strassen menggunakannya untuk menetapkan nilai tertinggi omega sebesar 2.48. Meskipun metode ini hanyalah salah satu langkah dalam perkalian matriks besar, ini adalah salah satu langkah terpenting karena para peneliti terus menyempurnakannya.

Satu tahun kemudian, Winograd dan Don Coppersmith memperkenalkan algoritma baru yang melengkapi metode laser. Kombinasi alat ini telah ditampilkan dalam hampir semua upaya selanjutnya untuk mempercepat perkalian matriks.

Berikut adalah cara berpikir yang disederhanakan tentang bagaimana elemen-elemen yang berbeda ini cocok satu sama lain. Mari kita mulai dengan dua matriks besar, A dan B, yang ingin Anda kalikan. Pertama, Anda menguraikannya menjadi banyak submatriks, atau blok, yang kadang-kadang disebut lebih kecil. Selanjutnya, Anda dapat menggunakan algoritma Coppersmith dan Winograd untuk berfungsi sebagai semacam instruksi manual untuk menangani, dan pada akhirnya merakit, balok-balok tersebut. “Ini memberitahu saya apa yang harus dikalikan dan apa yang harus ditambahkan dan entri apa yang harus dimasukkan ke mana” dalam matriks produk C, kata Vassilevska Williams. “Itu hanyalah resep untuk membangun C dari A dan B.”

Namun ada kendalanya: Terkadang Anda mendapatkan blok yang memiliki entri yang sama. Membiarkannya di dalam produk sama saja dengan menghitung entri tersebut dua kali, jadi pada titik tertentu Anda perlu menghilangkan istilah duplikat tersebut, yang disebut tumpang tindih. Para peneliti melakukan hal ini dengan “membunuh” blok-blok yang mereka tempati – menetapkan komponen-komponennya sama dengan nol untuk menghapusnya dari perhitungan.

Di sinilah metode laser Strassen akhirnya berperan. “Metode laser biasanya bekerja dengan sangat baik dan umumnya menemukan cara yang baik untuk mematikan sebagian blok untuk menghilangkan tumpang tindih,” kata Le Gall. Setelah laser menghilangkan, atau “membakar”, semua tumpang tindih, Anda dapat membuat matriks produk akhir, C.

Menggabungkan berbagai teknik ini menghasilkan suatu algoritma untuk mengalikan dua matriks dengan jumlah perkalian yang sengaja dibuat pelit secara keseluruhan — setidaknya secara teori. Metode laser tidak dimaksudkan untuk praktis; ini hanyalah cara memikirkan cara ideal untuk mengalikan matriks. “Kami tidak pernah menjalankan metode ini [di komputer],” kata Zhou. “Kami menganalisisnya.”

Dan analisis itulah yang menghasilkan peningkatan terbesar pada omega dalam lebih dari satu dekade.

Kerugian Ditemukan

Makalah musim panas lalu, yang ditulis oleh Duan, Zhou dan Wu, menunjukkan bahwa proses Strassen masih bisa dipercepat secara signifikan. Itu semua karena sebuah konsep yang mereka sebut sebagai kerugian tersembunyi, yang terkubur jauh di dalam analisis sebelumnya – “akibat dari hilangnya terlalu banyak blok secara tidak sengaja,” kata Zhou.

Metode laser bekerja dengan memberi label pada balok yang tumpang tindih sebagai sampah, yang dijadwalkan untuk dibuang; blok lainnya dianggap layak dan akan disimpan. Namun, proses seleksinya agak acak. Sebuah blok yang dinilai sebagai sampah, pada kenyataannya, ternyata berguna. Hal ini bukanlah sesuatu yang mengejutkan, namun dengan memeriksa banyak dari pilihan acak ini, tim Duan menyimpulkan bahwa metode laser secara sistematis meremehkan blok: Lebih banyak blok harus disimpan dan lebih sedikit blok yang dibuang. Dan, seperti yang biasanya terjadi, lebih sedikit limbah menghasilkan efisiensi yang lebih besar.

“Mampu menyimpan lebih banyak blok tanpa tumpang tindih mengarah pada… algoritma perkalian matriks yang lebih cepat,” kata Le Gall.

Setelah membuktikan adanya kehilangan ini, tim Duan memodifikasi cara metode laser memberi label pada balok, sehingga mengurangi limbah secara signifikan. Hasilnya, mereka menetapkan batas atas baru untuk omega di sekitar 2.371866 — peningkatan dibandingkan batas atas sebelumnya di 2.3728596, ditetapkan pada tahun 2020 oleh Josh Alman dan Vassilevska Williams. Ini mungkin tampak seperti perubahan kecil, menurunkan batas hanya sekitar 0.001. Namun ini adalah satu-satunya peningkatan terbesar yang pernah dilihat para ilmuwan sejak tahun 2010. Sebagai perbandingan, hasil Vassilevska Williams dan Alman pada tahun 2020 hanya meningkat 0.00001 dibandingkan pendahulunya.

Namun yang paling menarik bagi para peneliti bukan hanya rekor baru itu sendiri – yang tidak bertahan lama. Hal ini juga merupakan fakta bahwa makalah ini mengungkapkan jalan baru untuk perbaikan yang, sampai saat itu, belum diketahui sama sekali. Selama hampir empat dekade, semua orang mengandalkan metode laser yang sama, kata Le Gall. “Kemudian mereka menyadari bahwa kami bisa berbuat lebih baik.”

Makalah yang diterbitkan pada bulan Januari 2024 menyempurnakan pendekatan baru ini, sehingga memungkinkan Vassilevska Williams, Zhou, dan rekan penulis mereka untuk lebih mengurangi kerugian yang tersembunyi. Hal ini menyebabkan peningkatan tambahan pada batas atas omega, menguranginya menjadi 2.371552. Penulis juga menggeneralisasi teknik yang sama untuk meningkatkan proses perkalian persegi panjang (n-oleh-m) matriks — prosedur yang dapat diterapkan dalam teori grafik, pembelajaran mesin, dan bidang lainnya.

Kemajuan lebih lanjut dalam hal ini sudah pasti terjadi, namun ada batasnya. Pada tahun 2015, Le Gall dan dua kolaborator terbukti bahwa pendekatan saat ini – metode laser yang dipadukan dengan resep Coppersmith-Winograd – tidak dapat menghasilkan omega di bawah 2.3078. Untuk melakukan perbaikan lebih lanjut, Le Gall berkata, “Anda perlu memperbaiki [pendekatan] asli Coppersmith dan Winograd yang tidak banyak berubah sejak tahun 1987.. " Namun sejauh ini, belum ada yang menemukan cara yang lebih baik. Bahkan mungkin tidak ada satu pun.

“Meningkatkan omega sebenarnya adalah bagian dari pemahaman masalah ini,” kata Zhou. “Jika kita dapat memahami masalahnya dengan baik, maka kita dapat merancang algoritma yang lebih baik untuk mengatasi permasalahan tersebut. [Dan] masyarakat masih dalam tahap awal untuk memahami masalah kuno ini.”