Geometria della degenerazione nello spazio del potenziale e della densità

Geometria della degenerazione nello spazio del potenziale e della densità

Timestamp: 9 febbraio 2023 9:26

Markus Penz1 e Robert van Leeuwen2

1Comunità di ricerca di base per la fisica, Innsbruck, Austria
2Dipartimento di Fisica, Centro di Nanoscienze, Università di Jyväskylä, Finlandia

Trovi questo documento interessante o vuoi discuterne? Scrivi o lascia un commento su SciRate.

Astratto

In un lavoro precedente [J. Chimica. Fis. 155, 244111 (2021)], abbiamo trovato controesempi al teorema fondamentale di Hohenberg-Kohn dalla teoria del funzionale densità in sistemi a reticolo finito rappresentati da grafici. Qui dimostriamo che ciò si verifica solo a densità molto particolari e rare, quelle in cui gli insiemi di densità derivanti da stati fondamentali degenerati, chiamati regioni di degenerazione, si toccano tra loro o si toccano il confine dell'intero dominio di densità. È stato dimostrato che le regioni di degenerazione hanno generalmente la forma dello scafo convesso di una varietà algebrica, anche nell'impostazione del continuo. La geometria che emerge tra le regioni di densità e i potenziali che le creano viene analizzata e spiegata con esempi che, tra le altre forme, caratterizzano la superficie romana.

Geometria della degenerazione nello spazio potenziale e densità PlatoBlockchain Data Intelligence. Ricerca verticale. Ai.

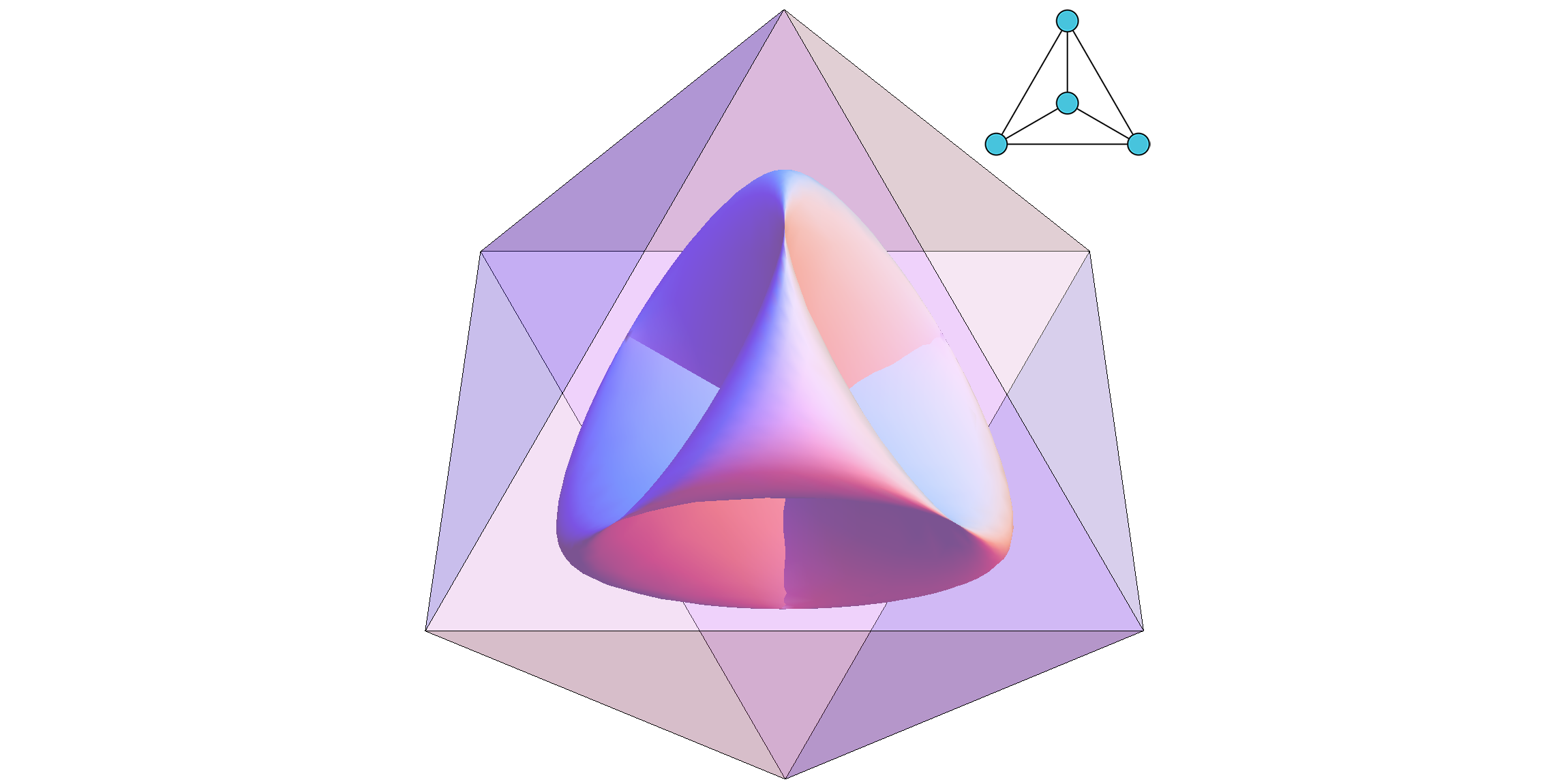
Immagine in primo piano: questa varietà algebrica, chiamata superficie romana, è formata da tutte le densità di una particella corrispondenti alle funzioni d'onda dall'estensione reale di un autospazio tridimensionale nello spazio di Hilbert di due particelle su un grafico tetraedrico. Le densità di tutti gli stati dello stesso autospazio formano l'involucro convesso di questa varietà. L'ottaedro attorno ad esso è il dominio di piena densità, dove gli angoli corrispondono agli estremi
densità (1, 1, 0, 0) e sue permutazioni sul grafico del tetraedro.

► dati BibTeX

► Riferimenti

, U. von Barth, Teoria di base del funzionale densità: una panoramica, Phys. Scr. 2004, 9 (2004).
https://​/​doi.org/​10.1238/​Physica.Topical.109a00009

, K. Burke e amici, L'ABC di DFT, (2007).
https://​/​dft.uci.edu/​doc/​g1.pdf

, RM Dreizler e EK Gross, Teoria del funzionale della densità: un approccio al problema quantistico a molti corpi (Springer, 2012).

, H. Eschrig, I fondamenti della teoria del funzionale della densità, 2a ed. (Springer, 2003).

, CA Ullrich, Teoria del funzionale densità dipendente dal tempo: concetti e applicazioni (OUP Oxford, 2011).

, CA Ullrich e Z. Yang, Un breve compendio della teoria del funzionale della densità dipendente dal tempo, Braz. J. fisico. 44, 154 (2014).
https:/​/​doi.org/​10.1007/​s13538-013-0141-2

, G. Vignale e M. Rasolt, Teoria del funzionale densità in forti campi magnetici, Phys. Rev. Lett. 59, 2360 (1987).
https: / / doi.org/ 10.1103 / PhysRevLett.59.2360

, G. Vignale, Mappatura dalle densità di corrente ai potenziali vettoriali nella teoria del funzionale della densità di corrente dipendente dal tempo, Phys. Rev. B 70, 201102 (2004).
https: / / doi.org/ 10.1103 / PhysRevB.70.201102

, M. Ruggenthaler, J. Flick, C. Pellegrini, H. Appel, IV Tokatly e A. Rubio, Teoria quantistica-elettrodinamica del funzionale densità: collegare l'ottica quantistica e la teoria della struttura elettronica, Phys. Rev.A90, 012508 (2014).
https: / / doi.org/ 10.1103 / PhysRevA.90.012508

, CA Ullrich e W. Kohn, Degenerazione nella teoria del funzionale della densità: topologia negli spazi v e n, Phys. Rev. Lett. 89, 156401 (2002).
https: / / doi.org/ 10.1103 / PhysRevLett.89.156401

, L. Garrigue, Alcune proprietà della mappa dello stato potenziale-terra nella meccanica quantistica, Commun. Matematica. Fis. 386, 1803 (2021).
https:/​/​doi.org/​10.1007/​s00220-021-04140-9.pdf

, DP Arovas, E. Berg, SA Kivelson e S. Raghu, Il modello Hubbard, Annu. Rev. Condens. Fisica della materia 13, 239 (2022).
https: / / doi.org/ 10.1146 / annurev-conmatphys-031620-102024

, M. Qin, T. Schäfer, S. Andergassen, P. Corboz e E. Gull, Il modello Hubbard: una prospettiva computazionale, Annu. Rev. Condens. Fisica della materia 13, 275 (2022).
https: / / doi.org/ 10.1146 / annurev-conmatphys-090921-033948

, F. Flores, D. Soler-Polo e J. Ortega, Una descrizione unificata locale-orbitale chiusa degli effetti dft e a molti corpi, J. Phys. Condensa. Materia 34, 304006 (2022).
https://​/​doi.org/​10.1088/​1361-648X/​ac6eae

, M. Penz e R. van Leeuwen, Teoria del funzionale densità sui grafici, J. Chem. Fis. 155, 244111 (2021).
https: / / doi.org/ 10.1063 / 5.0074249 mila

, EH Lieb, Funzionali di densità per sistemi di Coulomb, Int. J. Chimica quantistica. 24, 243 (1983).
https: / / doi.org/ 10.1002 / qua.560240302

, EI Tellgren, A. Laestadius, T. Helgaker, S. Kvaal e AM Teale, Campi magnetici uniformi nella teoria del funzionale densità, J. Chem. Fis. 148, 024101 (2018).
https: / / doi.org/ 10.1063 / 1.5007300 mila

, M. Penz, EI Tellgren, MA Csirik, M. Ruggenthaler e A. Laestadius, La struttura della mappatura del potenziale di densità. Parte I: teoria del funzionale densità standard, prestampa di arXiv (2022), arXiv:2211.16627 [fisica.chem-ph].
arXiv: 2211.16627

, M. Lewin, EH Lieb e R. Seiringer, Funzionali universali nella teoria del funzionale della densità, preprint di arXiv (2019), arXiv:1912.10424 [math-ph].
arXiv: 1912.10424

, L. Garrigue, Continuazione unica per operatori di Schrödinger a molti corpi e teorema di Hohenberg-Kohn, Math. Fis. Anale. Geom. 21, 27 (2018).
https: / / doi.org/ 10.1007 / s11040-018-9287-z

, I. Bárány e R. Karasev, Note sul numero di Carathéodory, Discrete Comput. Geom. 48, 783 (2012).
https: / / doi.org/ 10.1007 / s00454-012-9439-z

, MC Beltrametti, E. Carletti, D. Gallarati e G. Monti Bragadin, Lezioni su curve, superfici e varietà proiettive (European Mathematical Society, 2009).

, J. Harris, Geometria algebrica: un primo corso (Springer, 1992).

, WLF Degen, I tipi delle superfici triangolari di Bézier, Atti del 6° Convegno IMA sulla Matematica delle Superfici, 153 (1994).
https: / / doi.org/ 10.5555 / 646872.709694 mila

, L. Garrigue, Costruire potenziali di Kohn-Sham per stati fondamentali ed eccitati, Arch. Meccanismo razionale. Anale. 245, 949 (2022).
https:/​/​doi.org/​10.1007/​s00205-022-01804-1

, F. Apéry, Modelli del piano proiettivo reale (Vieweg, 1987).

, E. Fortuna, R. Frigerio e R. Pardini, Geometria proiettiva: problemi risolti e revisione della teoria, vol. 104 (Springer, 2016).

, T. Sederberg e D. Anderson, patch di superficie Steiner, IEEE Comput. Grafico. Appl. 5, 23 (1985).
https://​/​doi.org/​10.1109/​MCG.1985.276391

, A. Coffman, A. Schwartz e C. Stanton, L'algebra e la geometria di Steiner e altre superfici quadraticamente parametrizzabili, Comput. Aiutato Geom. Des. 13, 257 (1996).
https:/​/​doi.org/​10.1016/​0167-8396(95)00026-7

, C. Michel, Compléments de géométrie moderne (Vuibert, 1926).

, A. Clebsch, Ueber die Steinersche Fläche. Journal für die reine und angewandte Mathematik 67, 1 (1867).

, C. Cayley, Sulla superficie di Steiner, Proc. Londra. Matematica. Soc. 1, 14 (1873).
https: / / doi.org/ 10.1112 / PLMS / s1-5.1.14

, E. Lacour, Sur la surface de Steiner, Nouvelles annales de mathématiques: Journal des candidats aux écoles polytechnique et normale 17, 437 (1898).

, D. Hilbert e S. Cohn-Vossen, Geometria e immaginazione, vol. 87 (American Mathematical Society, 2021).

, G. Liu, M. Pi, L. Zhou, Z. Liu, X. Shen, X. Ye, S. Qin, X. Mi, X. Chen, L. Zhao, et al., Realizzazione fisica della superficie topologica romana mediante polarizzazione ferroelettrica indotta dallo spin nel reticolo cubico, Nature Comm. 13, 2373 (2022).
https: / / doi.org/ 10.1038 / s41467-022-29764-w

, V. Barbu e T. Precupanu, Convessità e ottimizzazione negli spazi di Banach, 4a ed. (Springer, 2012).

, S. Kvaal, U. Ekström, AM Teale e T. Helgaker, Formulazione differenziabile ma esatta della teoria del funzionale densità, J. Chem. Fis. 140, 18A518 (2014).
https: / / doi.org/ 10.1063 / 1.4867005 mila

, A. Laestadius, M. Penz, EI Tellgren, M. Ruggenthaler, S. Kvaal e T. Helgaker, Iterazione generalizzata di Kohn-Sham sugli spazi di Banach, J. Chem. Fis. 149, 164103 (2018).
https: / / doi.org/ 10.1063 / 1.5037790 mila

, M. Levy, Densità elettroniche alla ricerca di hamiltoniani, Phys. Rev. A 26, 1200 (1982).
https: / / doi.org/ 10.1103 / PhysRevA.26.1200

, F. Rellich, Störungstheorie der Spektralzerlegung, I. Mitteilung, Mathematische Annalen 113, 600 (1937).
https: / / doi.org/ 10.1007 / BF01571652

, F. Rellich, Teoria delle perturbazioni dei problemi agli autovalori (Gordon and Breach Science Publishers, 1969).

, T. Kato, Teoria delle perturbazioni per operatori lineari (Springer, 1995).

, M. Penz, A. Laestadius, EI Tellgren e M. Ruggenthaler, Convergenza garantita di un'iterazione Kohn-Sham regolarizzata in dimensioni finite, Phys. Rev. Lett. 123, 037401 (2019).
https: / / doi.org/ 10.1103 / physrevlett.123.037401

, M. Penz, A. Laestadius, EI Tellgren, M. Ruggenthaler e PE Lammert, Erratum: Convergenza garantita di un'iterazione Kohn-Sham regolarizzata in dimensioni finite, Phys. Rev. Lett. 125, 249902 (2020).
https: / / doi.org/ 10.1103 / PhysRevLett.125.249902

, A. Laestadius, EI Tellgren, M. Penz, M. Ruggenthaler, S. Kvaal e T. Helgaker, Teoria di Kohn-Sham con correnti paramagnetiche: compatibilità e differenziabilità funzionale, J. Chem. Calcolo della teoria. 15, 4003 (2019).
https: / / doi.org/ 10.1021 / acs.jctc.9b00141

, A. Laestadius e EI Tellgren, Mappatura della funzione d'onda della densità nella teoria del funzionale densità di corrente degenerata, Phys. Rev. A 97, 022514 (2018).
https: / / doi.org/ 10.1103 / PhysRevA.97.022514

Citato da

Questo documento è pubblicato in Quantum sotto il Creative Commons Attribuzione 4.0 Internazionale (CC BY 4.0) licenza. Il copyright rimane dei detentori del copyright originali come gli autori o le loro istituzioni.

Timestamp:

Di più da Diario quantistico