La prova dell'informatica a sorpresa stordisce i matematici

Domenica 5 febbraio, Olof Sisask e Thomas Bloom hanno ricevuto un'e-mail contenente una straordinaria scoperta sul più grande problema irrisolto nel loro campo. Zander Kelley, uno studente laureato dell'Università dell'Illinois, Urbana-Champaign, aveva inviato Sisask e Bloom un articolo che aveva scritto con Raghu Meka dell'Università della California, Los Angeles. Sia Kelley che Meka erano scienziati informatici, un mondo intellettuale separato dalla combinatoria additiva studiata da Sisask e Bloom.

“La mia mente era semplicemente sbalordita. Tipo, aspetta, l'hanno fatto davvero? ha detto Sisask, docente all'Università di Stoccolma. Kelley e Meka, estranei al campo della combinatoria, hanno affermato di aver trovato un nuovo limite – e notevolmente più basso – sulla dimensione di un insieme di numeri interi in cui non tre di essi siano equidistanti (escludendo combinazioni come 3, 8 e 13). o 101, 201 e 301).

L’affermazione di Kelley e Meka ha infranto il record precedente, raggiunto nel 2020 da Sisask e Bloom, ricercatore presso l'Università di Oxford. "Il lavoro di Bloom e Sisask - un lavoro molto forte che è stato - ha davvero dato l'impressione di essere estremamente difficile da migliorare", ha detto Ben Green, un collega di Bloom a Oxford. "Sembrava molto bloccato dov'era."

Sebbene sia Bloom che Sisask avessero altre questioni urgenti di cui occuparsi nel momento in cui hanno ricevuto l'e-mail - Bloom aveva appena adottato un cucciolo, mentre Sisask era nel bel mezzo del trasloco - si sono subito messi al lavoro per verificare il nuovo documento.

Nel giro di pochi giorni Bloom e Sisask si convinsero che la nuova prova era corretta. Sisask lo ha definito “il più grande risultato ottenuto nella zona negli ultimi 20 anni”. Ansiosi che gli altri apprezzassero le idee di Kelley e Meka, hanno redatto la bozza una relazione spiegando la dimostrazione in termini più familiari ai matematici.

Meka ha detto che la risposta della comunità è stata “più positiva di quanto pensassi. È incredibile vedere tutti i feedback”.

Progresso prolungato

Le sequenze di numeri equidistanti che Kelley e Meka cercarono di evitare sono chiamate progressioni aritmetiche. Possono durare all'infinito o contenere solo pochi termini. Kelley e Meka si sono concentrati su progressioni composte da soli tre numeri, seguendo una linea di ricerca spesso riconducibile a a carta 1936 di Paul Erdős e Paul Turán.

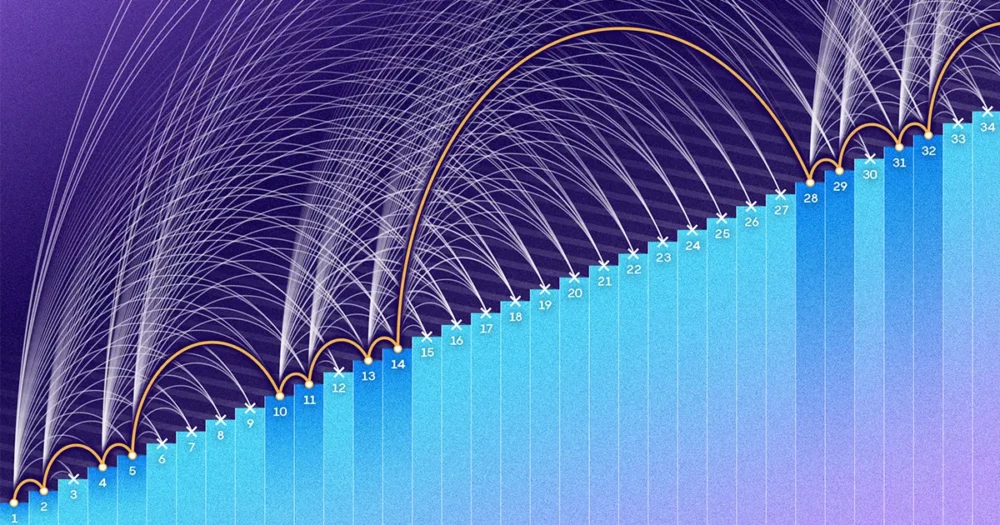
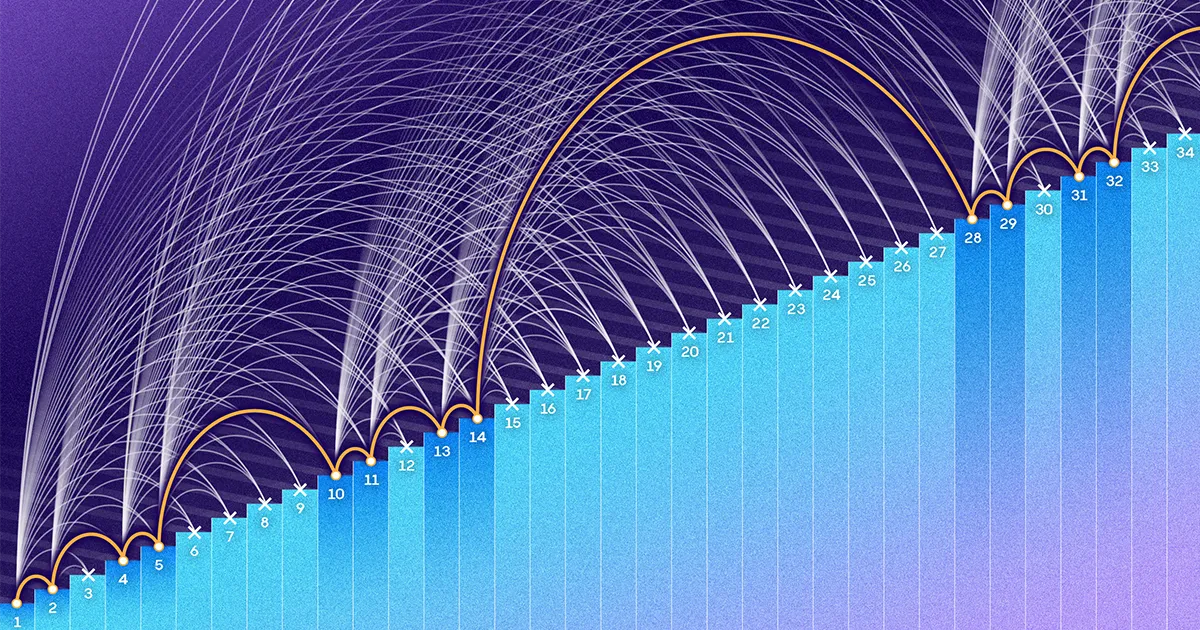
Erdős e Turán volevano sapere quanti numeri sono inferiori a un certo limite N può essere inserito in un insieme senza creare progressioni aritmetiche di tre termini. N potrebbe essere 1,000, 1 milione o un numero inimmaginabilmente enorme. Lo hanno ipotizzato come N crescesse, un insieme senza progressioni di tre termini dovrebbe diventare incredibilmente scarso. Creare un set del genere sarebbe come collezionare scarpe insistendo sul fatto che non esistono due paia dello stesso colore. Forse potresti continuare per sempre, ma man mano che la tua collezione diventasse più grande, ti ritroveresti ad aggiungerla a un ritmo sempre più lento.

"C'è una struttura che apparirà nel set, non importa come lo scegli", ha spiegato Meka. "Quanto è grande il set di cui hai veramente bisogno per garantire di avere questa struttura lì dentro?"

Nel 1946, Félix Behrend trovato un modo per costruire insiemi di numeri compresi tra 1 e N senza produrre alcuna progressione di tre termini. Il suo metodo ha prodotto set sempre più grandi N lo fece, ma dolorosamente lentamente. Quando N è 100,000, l’insieme di Behrend contiene solo 171 elementi. Quando N è 1 milione, il suo insieme ha 586 numeri, meno dello 0.06% dei numeri compresi tra 1 e 1 milione.

Gli insiemi di Behrend offrivano ai matematici un terreno su cui lavorare: l’insieme più grande senza una progressione di tre termini avrebbe dovuto essere grande almeno quanto quello di Behrend. Nel 1953 Klaus Roth previsto un massimale, trovando una soglia oltre la quale un insieme deve inevitabilmente contenere una progressione di tre termini.

Roth aveva dimostrato la congettura di Erdős e Turán dimostrandola come N diventa più grande, un insieme senza progressioni di tre termini comprenderà una frazione sempre più piccola dei numeri compresi tra 1 e N. Ma il tetto di Roth era molto lontano dal pavimento di Behrend. Behrend aveva dimostrato che lo 0.06% degli elementi compresi tra 1 e 1 milione potrebbe rientrare in un insieme privo di progressione. Sebbene la formula di Roth sia difficile da calcolare con precisione, non è neanche lontanamente così bassa: una stima approssimativa fissa un limite alla percentuale a circa il 40%.

Ma più importante di questo particolare divario è stato il comportamento complessivo delle due formule. Traccia la frazione di elementi tra 1 e N che ciascuna formula rappresenta, e vedrai il numero di Behrend ridursi rapidamente a zero N cresce. La frazione di Roth, invece, scivola verso lo zero, ma lentamente e dolcemente. Le due curve hanno forme molto diverse e la vera proporzione degli elementi che si trovano in un insieme senza progressioni aritmetiche potrebbe, per quanto ne sapevano i matematici, trovarsi ovunque tra loro.

A partire dagli anni ’1980, “c’è stata una lunga sequenza di miglioramenti, col senno di poi, abbastanza incrementali da parte di un gran numero di matematici veramente famosi”, ha detto Green. Di tanto in tanto, qualcuno abbassava di un pelo o due il limite superiore di Roth, e alla fine si abbassava considerevolmente. Il limite inferiore di Behrend, al contrario, non si è mosso per decenni. I matematici iniziarono a pensare che Behrend avrebbe potuto non essere lontano dalla vera risposta, ha detto Bloom.

Fino all’arrivo del documento di Kelley e Meka, all’inizio del 2023, la dimensione massima di un set senza progressione era definita dal basso dalla formula di Behrend e dall’alto da quella di Bloom e Sisask. L’articolo di Bloom e Sisask del luglio 2020 aveva superato la soglia critica “logaritmica” dimostrando che un insieme privo di progressione deve avere sostanzialmente meno di N/(tronco d'albero N) elementi. Ma il loro risultato era ancora molto al di sopra di quello di Behrend. Il nuovo limite superiore di Kelley e Meka è drasticamente più vicino al livello minimo fissato da Behrend.

"Meka e Kelley hanno in un certo senso scavalcato tutto questo progresso incrementale", ha affermato Terence Tao, un eminente matematico dell'UCLA.

La loro formula è quasi la stessa di Behrend, con solo pochi parametri modificati. COME N avvicina all'infinito, un grafico della formula di Kelley e Meka alla fine si stabilizzerà in una curva che assomiglia alla curva di Behrend. "Qualsiasi limite di quella forma prima sembrava un sogno impossibile", ha detto Bloom.

"Ero davvero sconcertato dal fatto che avessero apportato un tale miglioramento", ha detto Green.

Una virata diversa

 Sebbene Kelley e Meka non si fossero mai avventurati completamente nella ricerca matematica pura, le progressioni aritmetiche erano loro familiari quando iniziarono. In generale, gli informatici “cercano avidamente tecniche che possano funzionare per risolvere i nostri problemi”, ha detto Kelley. Gli strumenti storicamente utilizzati per studiare la dimensione di un insieme privo di progressione sono diventati ampiamente utilizzati nel sottocampo informatico della teoria della complessità. Il problema di restringere la dimensione di un tale insieme è ben noto ai teorici della complessità come esempio tipico di applicazione di tecniche che sondano la struttura interna degli insiemi.

Alla fine del 2021, Kelley e Meka stavano analizzando le possibilità che una squadra di giocatori in un determinato gioco cooperativo riuscisse a vincere, un tipo standard di problema informatico. Hanno pensato che le tecniche ricavate dalla ricerca sulla dimensione delle serie prive di progressione avrebbero potuto essere utili. Ma hanno trovato più semplice studiare direttamente quelle tecniche piuttosto che applicarle al gioco cooperativo. "La mia migliore idea su come fare progressi su questo problema [era] quella di migliorare effettivamente lo strumento stesso, non di usarlo in un modo più intelligente", ha detto Kelley.

"Ad un certo punto, abbiamo deciso di lavorare direttamente su questa questione", ha ricordato Meka. Sei mesi dopo, i due ricercatori avevano definito la loro strategia e dovevano solo capire come applicare il loro metodo al problema in questione.

Per vedere come sono arrivati ​​al nuovo limite superiore, prendi qualsiasi serie di numeri tra 1 e N. Chiamalo A. La densità di A è la percentuale dei numeri compresi tra 1 e N che include. Poiché ci sono molte possibili progressioni aritmetiche tra 1 e N, se non scegli gli elementi di A con attenzione, qualsiasi A con alta densità conterrà probabilmente molte progressioni aritmetiche.

Nella loro dimostrazione, Kelley e Meka lo immaginavano A avevano poche o nessuna progressione aritmetica e tentarono di tracciarne le conseguenze. Se A era sufficientemente denso, hanno dimostrato che l’assenza di progressioni necessitava di un livello di struttura interna A ciò risulterebbe inevitabilmente in una contraddizione, nel senso che A deve, dopo tutto, contenere almeno una progressione.

Per comprendere quella struttura, hanno considerato il set A + A, che consiste di tutti i numeri ottenuti sommando due elementi di A. Hanno notato che se A contiene relativamente poche progressioni aritmetiche, ciò implica una ridondanza tra gli elementi di A + A: Diverse coppie di numeri da A spesso si sommano allo stesso numero.

La densità può essere definita non solo rispetto a tutti gli interi compresi tra 1 e N ma in confronto ad alcuni sottoinsiemi - diciamo solo gli interi pari in quell'intervallo, o solo i multipli di 3. Kelley e Meka hanno usato le ridondanze in A + A per trovare un sottoinsieme degli interi in cui gli elementi di A erano particolarmente comuni.

Se A contenesse un numero sproporzionato di multipli di 3, ad esempio, Kelley e Meka si concentrerebbero sulla parte che include multipli di 3. Hanno ripetuto questa strategia ancora e ancora. Ogni volta trovavano sottoinsiemi sempre più piccoli di numeri interi, su cui ALa densità di continuerebbe a crescere e crescere. Per esempio, A potrebbe contenere il 10% dei numeri interi compresi tra 1 e N, il 15% dei multipli di 3 in quell'intervallo e il 25% dei multipli pari di 3.

Succede qualcosa di interessante quando A è grande. Se la procedura viene ripetuta, la densità di A su alcuni sottoinsiemi supera il 100%. Questo, ovviamente, è impossibile. A potrebbe contenere, ad esempio, tutti i multipli di 24, ma non può contenerne più di tutti. Questo paradosso sorge solo se A è abbastanza grande per cominciare, ma quando lo fa, significa presupporre che A non contiene alcuna progressione aritmetica deve essere stato sbagliato.

È un "argomento vantaggioso per tutti", quando A è grande, ha detto Meka. O A include molte progressioni aritmetiche o c'è molta ridondanza A + A - nel qual caso potrebbero utilizzare la procedura di ricerca dei sottoinsiemi (chiamata "strategia di incremento della densità") per dimostrare che una progressione deve apparire in A. Anche se la strategia di incremento della densità è un modello ben utilizzato nel settore, Kelley e Meka sono riusciti a farla funzionare per i più piccoli Aè più che mai. Con ciò, hanno scoperto un nuovo limite massimo per le dimensioni di un set senza progressione.

Kelley e Meka hanno creato una combinazione unica di idee dal progetto di incremento della densità. Invece di elaborare una struttura completamente nuova, hanno ripensato il modo in cui hanno trovato il loro denso sottoinsieme. Per questo, hanno utilizzato una tecnica chiamata “sifting”, che consiste nello spostare il set di una quantità costante, intersecarlo con se stesso e ripetere il processo molte, molte volte. Ciò che rimane, dopo molti cicli di intersezione, è un insieme altamente strutturato con proprietà prevedibili. Sebbene il sifting sia stato utilizzato in altri articoli, non era mai stato provato sul problema della progressione a tre termini.

Guardando indietro

Kelley e Meka hanno abbassato il limite di dimensione di un set senza progressione di una quantità scioccante inserendo strumenti trascurati come il setacciamento nei metodi tradizionali. "Kelley e Meka ci hanno mostrato che in qualche modo queste tecniche, che erano là fuori allo scoperto, erano semplicemente molto più potenti di quanto sospettassimo", ha detto Bloom. Alla luce della ritrovata efficacia di questi strumenti, ha aggiunto, “dobbiamo tornare indietro e rivisitare tutto”.

La strategia di incremento della densità è apparsa per la prima volta nell’articolo di Roth 70 anni fa e da allora è stata utilizzata nella maggior parte degli articoli sulle progressioni aritmetiche. Green fu sorpreso dal fatto che il quadro potesse essere utilizzato per dimostrare un limite così basso come quello di Kelley e Meka. "Pensavo che sarebbe stato necessario qualcosa di completamente, radicalmente diverso", ha detto.

Kelley è entusiasta di continuare la sua incursione nella matematica. "Non mi mancano speranze e sogni su molti problemi diversi che considererei almeno spiritualmente legati a questo", ha detto.

Il fatto che Kelley e Meka siano riusciti a individuare la forza di idee un tempo trascurate dimostra la natura spesso discontinua del progresso matematico, una qualità che per Tao è più una benedizione che una maledizione. “Non è sempre vero che la matematica diventa sempre più difficile e sempre più difficile”, ha detto. "Meno male."