המשולש הקטן והגדול ביותר רק הלך וקטן | מגזין קוונטה

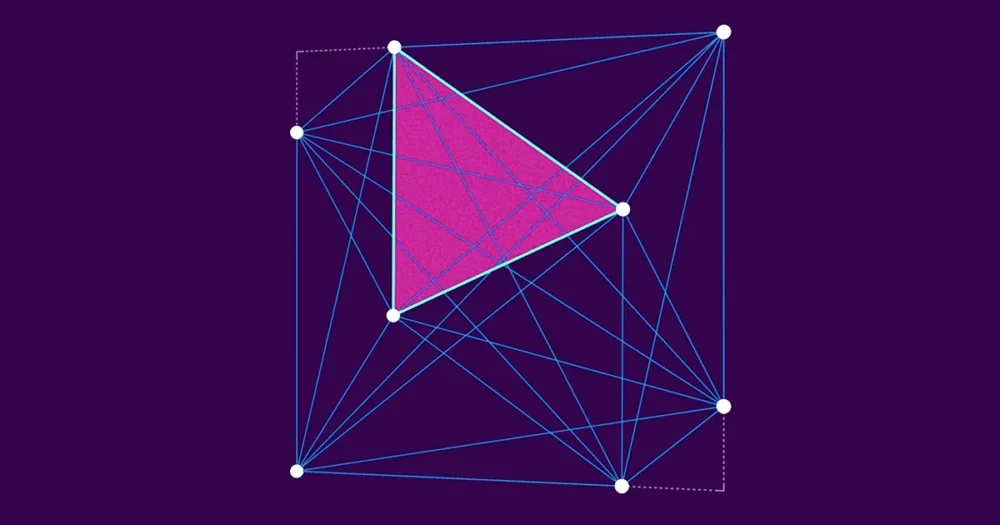
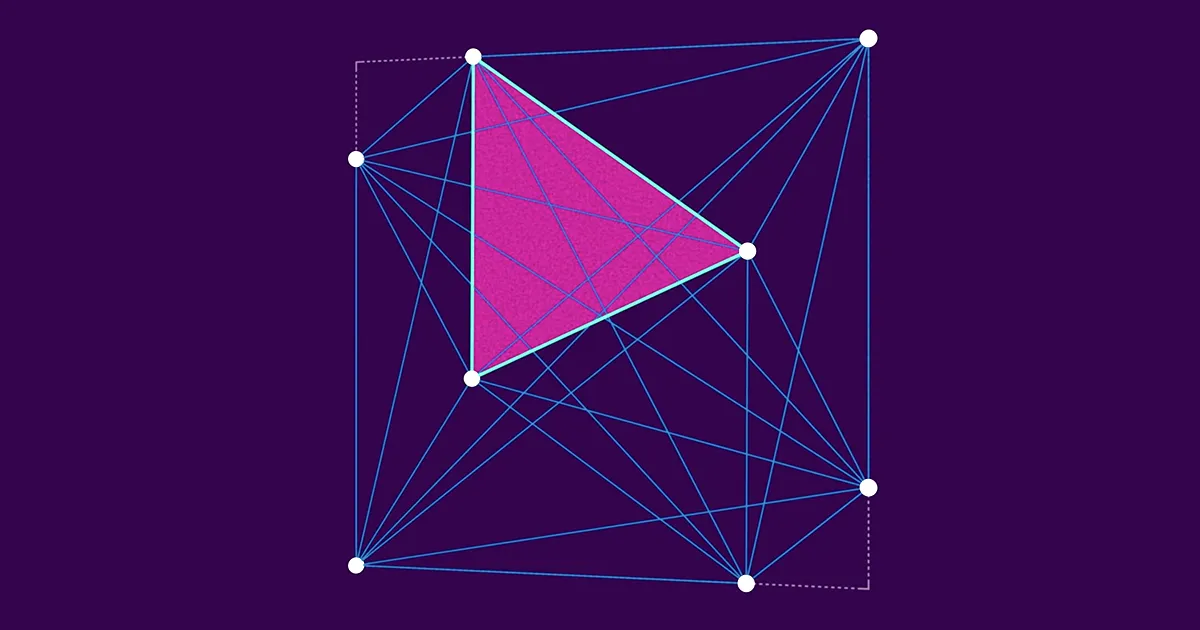
שקול ריבוע עם חבורה של נקודות בפנים. קח שלוש מהנקודות האלה, ותוכל ליצור משולש. ארבע נקודות מגדירות ארבעה משולשים שונים. עשר נקודות מגדירות 120 משולשים. המספרים גדלים במהירות משם - 100 נקודות מגדירות 161,700 משולשים שונים. לכל אחד מהמשולשים הללו, כמובן, יש אזור מסוים.

הנס היילברון, מתמטיקאי גרמני שברח מארצו לפני מלחמת העולם השנייה והתיישב באנגליה, חשב על המשולשים הללו בסוף שנות הארבעים כשראה קבוצת חיילים מחוץ לחלונו. נראה שהחיילים לא בהרכבה, מה שגרם לו לחשוב: אם יש n חיילים בתוך ריבוע, מה גודלו של המשולש הקטן ביותר האפשרי המוגדר על ידי שלושה מהם? היילברון תהה איך אפשר לסדר את החיילים (או, לשם הפשטות המתמטית, נקודות) כדי למקסם את גודל המשולש הקטן ביותר.

הבעיה היא פשוטה להצהיר, אבל ההתקדמות בבעיית משולש היילברון, כפי שנקראה, נעצרה, והתוצאות התייבשו לחלוטין בשנות ה-1980. ואז במאי האחרון, שלושה מתמטיקאים - אלכס כהן, קוסמין פוהואטה ו דמיטרי זכרוב - הכריז א כובע חדש על גודל המשולש הקטן ביותר. "אני חושב שזו תוצאה מדהימה", אמר אנתוני קארברי, מתמטיקאי מאוניברסיטת אדינבורו.

חוקרים המשיכו לעבוד על בעיית משולש היילברון לאורך השנים, למרות ההמתנה הארוכה להתקדמות, מונעת מסבך הקישורים שלה לתחומי מתמטיקה אחרים. "הדברים שהוא קשור כדי לגרום לזה להתעורר לחיים", אמר פוהואטה, פרופסור באוניברסיטת אמורי באטלנטה. זה קשור קשר הדוק לבעיות בנושא צורות מצטלבות, אשר בתורן מתחברות הן לתורת המספרים והן לניתוח פורייה - חקר פונקציות מסובכות הבנויות מגלים פשוטים.

כהן, סטודנט לתואר שני במכון הטכנולוגי של מסצ'וסטס, נתקל בשנה שעברה ברשת הקשרים הזו. הוא עיין בסקר ישן של בעיית משולש היילברון מאת קלאוס רוט, פליט נוסף מהנאצים שנמלט לבריטניה כילד. (רוט, שמת ב-2015, היה המתמטיקאי הבריטי הראשון שזכה במדליית פילדס.)

כהן הדמייה את הרעיונות מהסקר של רוט בתמונה פשוטה: ריבוע שנחצה בשתי רצועות עבות, עם קו דק באמצע כל אחת מהן. כשבחן את הדיאגרמה שלו, הבין כהן שזה עשוי להתחבר לרעיונות שיועצו, לארי גוט, העלה במפגש האחרון של קבוצת הקריאה. אבל גוט לא דיבר על משולשים בכלל.

"הבנתי מהר מאוד ששתי השיטות הללו שוות במהותן", אמר כהן. "ממש התלהבתי מבעיית המשולשים."

יום אחד בחדר המשותף של המחלקה למתמטיקה של MIT, כהן גילה במפתיע כי פוהואטה, שהגיע לשאת הרצאה, וזכרוב, סטודנט אחר לתואר שני ב-MIT, עבדו גם הם על בעיית משולש היילברון. מה שכן, הם מצאו את אותו קישור. השלושה החלו לשתף פעולה. שבעה חודשים לאחר מכן, הם עשו את פריצת הדרך שלהם. המאמר שלהם מביא עוד תחומים חדשים במתמטיקה. "הם משתמשים בכמות עצומה של מכונות ותובנות שונות", אמר תומס בלום מאוניברסיטת אוקספורד, שאמר שהוא מצפה שהמאמר החדש "יעורר רנסנס" של התקדמות בבעיית המשולשים.

נפלה השערה

על ידי הצבת שלוש נקודות קרוב מאוד זו לזו, אתה יכול בקלות להפוך את המשולש הקטן ביותר בסידור קטן באופן שרירותי. (במקרה הקיצוני ביותר, שלוש נקודות בקו אחד עם השני יוצרות משולש עם שטח אפס.) אבל הניסיון לשמור על המשולש הקטן ביותר הוא מסובך יותר. ככל שאתה ממשיך להוסיף עוד נקודות, המשולש הקטן ביותר נאלץ להיות די קטן - נקודות חדשות יכולות להיות רחוקות כל כך מהקיימות. קל יחסית להראות שלמשולש הקטן ביותר לא יכול להיות שטח גדול מ-1/(n − 2) על ידי פיצול הריבוע למשולשים שאינם חופפים.

אבל היילברון חשב שהגבול קטן עוד יותר מזה. הוא ניחש שלא משנה איך הנקודות מסודרות בריבוע, לא יכול להיות משולש קטן ביותר עם שטח גדול מסביבות 1/n², מספר שמתכווץ הרבה יותר מהר כמו n גדל.

הוא טעה.

בשנת 1980, המתמטיקאים ההונגרים יאנוס קומלוס, יאנוס פינץ ואנדרה שמרדי מצא דפוס של נקודות שלמשולש הקטן ביותר שלהן היה שטח גדול יותר מ-1/n². במאמר נפרד שפורסם בערך באותו זמן, הם גם הראו שאי אפשר לסדר n נקודות כדי ליצור משולש קטן ביותר שגדול מסביבות 1/n^8/7. כאשר n הוא גדול, זה הרבה יותר קטן מ-1/n, אבל הרבה יותר מ-1/n².

תוצאות אלו עמדו על 40 שנה. "שיפור [הגבול] בשני הכיוונים היה קשה להפליא ודרש הרבה ניתוח טכני וכושר המצאה", אמר בלום.

"אתה מאוד מאוד מהר נתקע בבוץ שלם של דברים", הוסיף קארברי.

בעוד שהבנייה שהתגלתה ב-1980 נותרה זו עם המשולש הקטן ביותר הידוע, כהן, פוהוטה וזכרוב הצליחו, לראשונה מזה ארבעה עשורים, להוריד את הגבול העליון.

אבולוציה מתכנסת

בזמן שפגש את כהן, פוהוטה כבר עבד על בעיית משולש היילברון במשך שנתיים. בקיץ 2020, הוא הכניס סטודנטים למחקר קיץ באוניברסיטת ייל לעבוד על גרסאות גבוהות יותר של הבעיה - למשל, צמצום הצורות הגדולות ביותר בנפח הקטן ביותר המופיעות בין נקודות מפוזרות בקובייה תלת מימדית.

כחלק מהפרויקט הזה, Pohoata בחן מחדש את כל העבודה הקודמת על הבעיה. חזרה ל- 1951, רוט חילק את החיפוש אחר משולשים קטנים לשני חלקים: תחילה מצא זוג נקודות ליצירת בסיס המשולש, ולאחר מכן מצא נקודה שלישית להשלמת המשולש. האסטרטגיה מיסגרה בעצם את החיפוש אחר משולש קטן גדול ביותר כמחקר של נקודות ומלבנים מצטלבים - גישה ששוכללה ב-1972 על ידי וולפגנג שמידט.

בקריאת המאמר של שמידט, זיהה פוהוטה קשר לשיטה הגבוהה-נמוכה - טכניקה שפיתחו גוט ושותפי פעולה ב-2017 להערכת החפיפה בין אוסף של רצועות מלבניות לאוסף של דיסקים. "זה היה רגע פסיכולוגי חשוב עבורי", אמר.

בשנת 2021, פוהוטה העלה את רעיונותיו עם זכרוב. השניים החלו לפרסם יחד כשזכרוב היה עדיין סטודנט לתואר ראשון במוסקבה. "[זכרוב] עשה דברים יוצאי דופן כאילו הוא חוקר בכיר בגיל צעיר", אמר ג'ייקוב פוקס, מתמטיקאי מאוניברסיטת סטנפורד.

זכרוב היה בתחילה פסימי לגבי בעיית משולש היילברון. "חשבתי שבכן, ה-8/7 הזה נשאר שם למעלה 40 שנה, אז מי אני שאפצח את זה?" הוא אמר. "בעיקר רציתי להבין איך זה עובד".

לאחר שנתקלו זה בזה באוקטובר 2022, כהן, פוהוטה וזכרוב הצביעו במהרה על המכשול שעמו התמודדו קומלוס, פינץ ושמרדי מבלי לדעת. "יש סידור מאוד ספציפי של הנקודות שמוביל לתרחיש הגרוע ביותר שבו הם לא יכולים לעשות יותר מ-8/7", אמר כהן. "הנקודות יכולות להיות מרוכזות או לפרוסות. המקרה הגרוע ביותר הוא כאשר מדובר בשילוב כלשהו". להסדר הזה היו נקודות פרושות בקנה מידה גדול, אבל אם היית מגדילה את ריבועים זעירים בתוך ריבוע היחידה, היית רואה תבניות מסודרות.

כהן, פוהוטה וזכרוב הבינו שהם יכולים להתקדם על ידי לימוד המימד של מקבצי הנקודות הקטנים. עבור מי שאינם מתמטיקאים, מידות הן תמיד מספרים שלמים: גיליון נייר הוא דו מימדי; ללבנת חימר יש תלת מימד.

דברים יכולים להיות מוזרים כשחושבים על הממד של קבוצת נקודות. נקודה בודדת נחשבת בדרך כלל לאפס מימד. אבל לשתי קבוצות סופיות של נקודות יכולות להיות מבנים שונים לחלוטין. לאחד עשויות להיות 10 נקודות צועדות בצייתנות בקו ישר, בעוד שלאחר יש 10 נקודות מפוזרות על פני כל ריבוע היחידה.

כדי ללכוד את המבנה של אפילו קבוצות הנקודות המוזרות ביותר, המתמטיקאי של תחילת המאה ה-20 פליקס האוסדורף הגה רעיון חדש של מימד. לפי הגדרה זו, 10 נקודות בקו הן חד-ממדיות, בעוד ש-10 נקודות המפוזרות באופן שווה על פני ריבוע הן דו-ממדיות. אבל בעולם הזה, ממדים לא חייבים להיות מספרים שלמים, וקבוצה חד-ממדית יכולה להיות לא ליניארית אלא פרקטלית, עם שכבות אינסופיות של דפוסים מורכבים. בהתאם לפרטים של דפוסים אלה, אוספי נקודות יכולים אפילו להיות בעלי ממד שגדול מ-0 אך פחות מ-1.

כהן, פוהוטה וזכרוב חשפו א משפט 1953 מאת ג'ון מרסטרנד שניסח מחדש את האומדן של קומלוס, פינץ ושמרדי במונחים של מימד האוסדורף - אבל רק עבור ממדים גדולים מ-1. על מנת לשפר את האומדן, כהן, פוהוטה וזכרוב יצטרכו למצוא דרך כלשהי להכליל את התוצאה של מרסטרנד לקבוצות שהממד שלו היה קטן מ-1.

יצירת חיבורים

כהן, פוהוטה וזכרוב לא היו צריכים לחשוב הרבה. כפי שקרה, מאמר מאת טומאס אורפונן, פבלו שמרין ו הונג וואנג שזה היה זה עתה פורסם באינטרנט הרחיב את משפט 70 השנים של מרסטרנד לקבוצות שהממד שלהן היה קטן מ-1.

כהן לא למד על העיתון עד פברואר. ברגע שעשה זאת, הוא העביר את זה במהירות לפוהואטה ולזכרוב. בסוף מאי, הם פרסמו את העיתון שלהם באינטרנט, והוכיחו שהמשולש הקטן ביותר ביניהם n נקודות בריבוע יחידה לעולם לא יכולות להיות גדולות מ-1/n^{8 / 7 + 1 / 2000}.

שמרקין קרא את עיתון המשולש בגחמה לאחר שראה אותו הוכרז בטוויטר. הוא אפילו לא היה מודע לבעיית משולש היילברון לפני כן, אז הוא הופתע כאשר הבחין בהתייחסות להוכחה שלו. "זה לא יישום ישיר של מה שאנחנו עושים. יש בו הרבה עבודה מלאת תובנות, יצירתיות וטכניות", אמר. "בשבילי זו הייתה הרגשה נהדרת".

גם בלום התרשם. "יכולתי להסתכל על הנייר הזה הרבה זמן ומעולם לא חשבתי, הו, זה חל על בעיית המשולשים."

בעוד שהתוצאה החדשה משפרת את המעריך של קומלוס, פינץ ושמרדי רק בשבריר קטנטן, היא החיה מחדש את בעיית משולש היילברון שנמשכה זמן רב. "אתה יכול להסתכל על זה ולהגיד, פיהוק, פיהוק, פיהוק, זה לא נראה כל כך שונה ממה שהיה ידוע ב-1982. אבל הרבה מאוד זמן עבר מאז 1982", אמר קארברי.

על ידי שילוב שיטת הגבוה-נמוך ועבודותיהם של אורפונן, שרקין ו-ואנג, חשפו כהן, פוהוטה וזכרוב מערכת קשרים חדשה בין בעיית משולש היילברון לשאר המתמטיקה. כפי שאמר בלום, בעיית המשולש נחשבה כ"בעיה ממש נחמדה, ממש קשה שאנחנו לא יודעים מה לעשות. אבל הם אמרו שזה קשור לכמות עצומה של דברים אחרים".

יש המאמינים שהתשובה האמיתית לבעיית המשולש של היילברון לא תהיה גדולה בהרבה מהניחוש המקורי שלו של 1/n². "אם אני שם נקודות בצורה מובנית, אני נכשל; אם אני שם נקודות בצורה אקראית, אז אני נכשל. זה לא יכול להיות מובנה מדי, זה לא יכול להיות אקראי מדי, ולכן זה כנראה לא קיים", אמר בלום. אבל זכרוב מקווה לתשובה אחרת. האינטואיציות התומכות בתשובה של 1/n² הם "די משעממים", אמר. "מאוד הייתי מעדיף אם זה היה n^3/2".