量子力学のゲージ図

量子力学のゲージ図

タイムスタンプ：21年2024月6日43:XNUMX AM

ケビン・スレーグル

ライス大学、電気およびコンピュータ工学部、ヒューストン、テキサス州 77005 米国
カリフォルニア工科大学物理学科、パサデナ、カリフォルニア 91125、米国
量子情報・物質研究所およびウォルター・バーク理論物理学研究所、カリフォルニア工科大学、パサデナ、カリフォルニア州 91125、米国

この論文を興味深いと思うか、議論したいですか？ SciRateを引用するかコメントを残す.

抽象

局所的なハミルトニアンは局所的な時間ダイナミクスを示しますが、波動関数の振幅が局所的な運動方程式に従わないという意味で、この局所性はシュレディンガー図では明示的ではありません。我々は、量子力学のグローバルユニタリ不変性をローカルゲージ不変性に「ゲージ化」することによって、運動方程式において幾何学的局所性を明示的に達成できることを示す。つまり、期待値 $langle psi|A|psi rangle$ は、波動関数 $|psirangle から U |psirangle$ と演算子 $A から UAU^dagger$ に作用するグローバル ユニタリ変換の下では不変であり、それが可能であることを示します。このグローバルな不変性をローカルなゲージの不変性に測定します。これを行うには、波動関数を、空間 $J$ のパッチごとに 1 つずつ、ローカル波動関数 $|psi_Jrangle$ のコレクションに置き換えます。空間パッチのコレクションは、空間をカバーするために選択されます。たとえば、単一量子ビットまたは格子上の最近傍サイトとなるパッチを選択できます。空間パッチ $I$ と $J$ の隣接するペアに関連付けられた局所波動関数は、動的ユニタリ変換 $U_{IJ}$ によって互いに関連付けられます。ローカル波動関数は、そのダイナミクスがローカルであるという意味でローカルです。つまり、ローカル波動関数 $|psi_Jrangle$ と接続 $U_{IJ}$ の運動方程式は空間内で明示的にローカルであり、近くのハミルトニアン項にのみ依存します。 (局所波動関数は多体波動関数であり、通常の波動関数と同じヒルベルト空間次元を持ちます。)この量子力学の図は局所ゲージ不変性を示すため、ゲージ図と呼ばれます。単一の空間パッチの局所的なダイナミクスは相互作用画像に関連しており、相互作用ハミルトニアンは近くのハミルトニアン項のみで構成されます。また、明示的な局所性を一般化して、局所的な電荷とエネルギー密度の局所性を含めることもできます。

Quantum Dynamics PlatoBlockchain Data Intelligence のゲージ画像。垂直検索。あい。

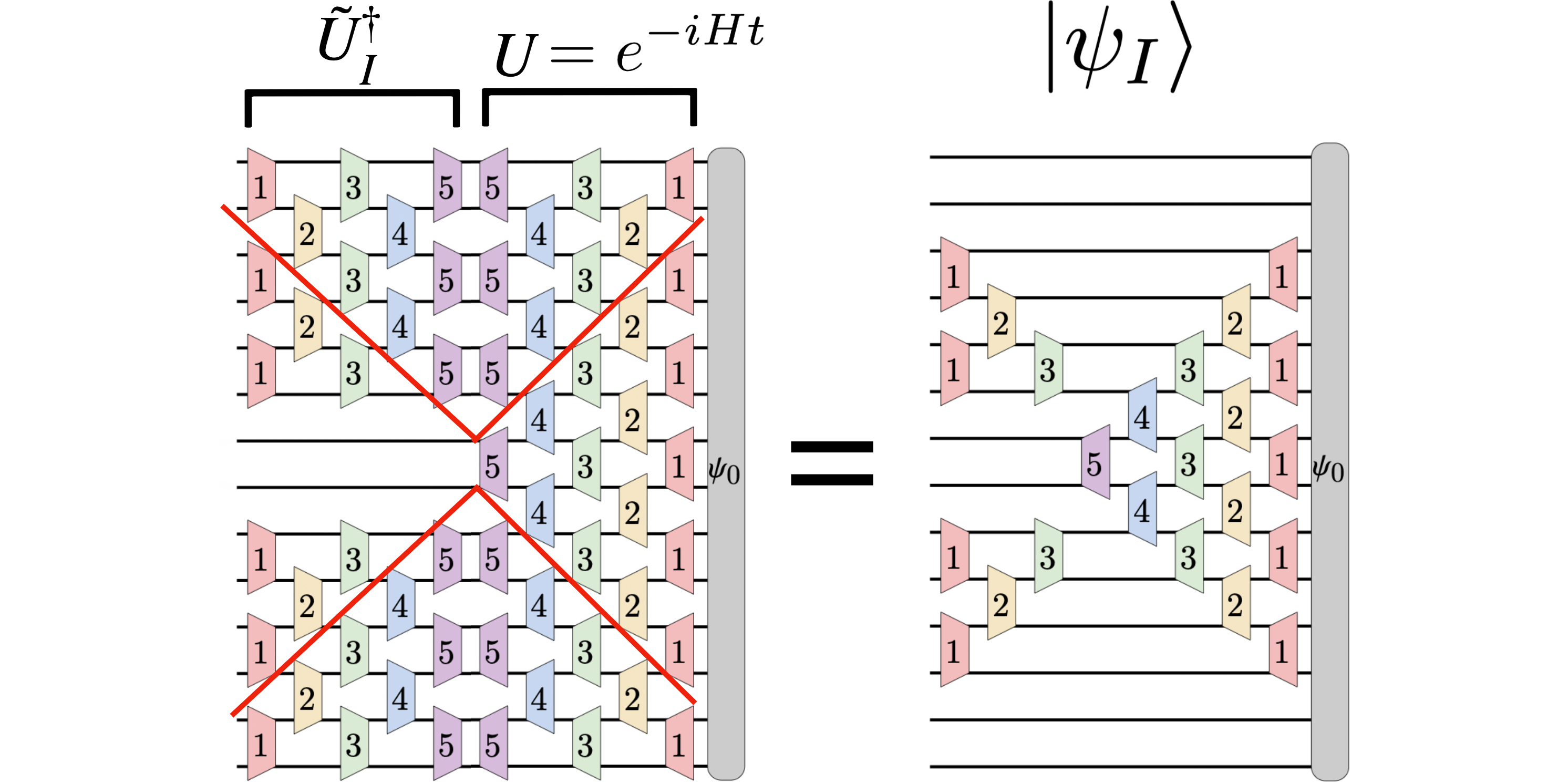
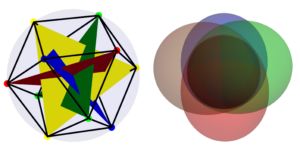
注目の画像: シュレディンガーの写真では、初期波動関数 $|psi_0rangle$ は時間 $t$ 後に $U(t) |psi_0rangle$ に進化します。ここで、$U(t) = e^{-iHt}$ はユニタリ時間発展です。オペレーター。代わりに、ゲージ画像では、空間内のサブセット (またはパッチ) $I$ に関連付けられたローカル波動関数 $|psi_I(t)rangle$ が考慮されます。時間発展した局所波動関数 $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ は、シュレーディンガーの波動関数 $|psi(t)rangle = U(t) |psi_0rangle から取得されます。 $ はユニタリー演算子 $tilde{U}_I^dagger(t)$ を介して、領域 $I$ の外側の時間発展を逆転させます。結果として、局所波動関数ダイナミクス $partial_I |psi_I(t)rangle$ は、領域 $I$ と重なる近くのハミルトニアン項にのみ依存します。この図は、これらのユニタリー演算子を量子回路として示しており、$U(t)$ からの時間発展のほとんどが $tilde{U}_I^dagger(t)$ で相殺され、砂時計の形の時間発展演算子だけが残ることを示しています。初期波動関数に作用します (図の右側)。この砂時計の形をした演算子は、ハイゼンベルクの絵にある光円錐形の演算子の成長に似ています。

人気の要約

量子力学の最も有名な 2 つの写真は、シュレディンガーとハイゼンベルクの写真です。シュレディンガーの図では、波動関数は時間とともに進化しますが、ハイゼンベルクの図では、波動関数は一定ですが、演算子は時間とともに進化します。この研究では、情報の局所性とゲージ理論と深い関係を持つ、量子力学の新しい図であるゲージ図を紹介します。

局所性について: ハイゼンベルクの絵の優れた利点は、局所性が運動方程式で明示されていることです。つまり、ローカル オペレーターの時間発展は、近くのローカル オペレーターの状態にのみ依存します。対照的に、シュレーディンガーの図では、局所性はこのように明示的ではありません。シュレーディンガーの図では、時間ダイナミクスが空間のあらゆる場所の演算子に依存する単一の波動関数が存在します。私たちの新しいゲージ画像は、シュレディンガーの波動関数と同じ情報を運ぶ「局所波動関数」を計算できるようにシュレディンガー画像を修正します。ゲージ画像内の局所波動関数の時間ダイナミクスは近くのハミルトニアン項にのみ依存すると予想されます。これにより、局所性が次の式で明示されます。運動方程式。この明示的な局所性を実現するために、ゲージ ピクチャは運動方程式にゲージ フィールドを追加します。

ゲージ理論は、大域対称性を持つハミルトニアン (またはラグランジアン) と、追加の動的ゲージ場を介して大域対称性が局所ゲージ対称性に置き換えられる別のハミルトニアンとの間に深いつながりを確立します。興味深いことに、シュレーディンガーの方程式 $ihbarpartial_t |psirangle = H |psirangle$ は、$|psirangle から U |psirangle$ への変換、および $H から UHU^dagger$ への変換によって与えられる大域的なユニタリ不変性を認めています。私たちの研究は、シュレーディンガー方程式のこの大域的不変性にゲージ理論を適用して、動的ゲージ場と局所的なゲージ不変性を備えた新しい運動方程式、つまりゲージ画像を取得することも可能であることを示しています。

►BibTeXデータ

►参照

【1] デヴィッド・ドイチュとパトリック・ヘイデン。 「もつれた量子システムにおける情報の流れ」。ロンドン王立協会議事録シリーズ A 456、1759 (2000)。 arXiv:quant-ph/9906007.
https：/ / doi.org/ 10.1098 / rspa.2000.0585
arXiv：quant-ph / 9906007

【2] マイケル・A・レビンとシャオガン・ウェン。 「ストリングネット凝縮: トポロジカル位相の物理メカニズム」。物理学。 Rev. B 71、045110 (2005)。 arXiv:cond-mat/ 0404617.
https：/ / doi.org/ 10.1103 / PhysRevB.71.045110
arXiv：cond-mat / 0404617

【3] T. センティル、アシュビン ヴィシュワナート、レオン バレンツ、スビル サクデフ、マシュー PA フィッシャー。 「非限定化された量子臨界点」。サイエンス 303、1490–1494 (2004)。 arXiv:cond-mat/ 0311326.
https：/ / doi.org/ 10.1126 / science.1091806
arXiv：cond-mat / 0311326

【4] 吉田紅さん。 「フラクタルスピン液体におけるエキゾチックな位相秩序」。物理学。 Rev. B 88、125122 (2013)。 arXiv:1302.6248。
https：/ / doi.org/ 10.1103 / PhysRevB.88.125122
arXiv：1302.6248

【5] ケビン・ハートネット。 「行列の乗算は神話上の目標に少しずつ近づいています」。クアンタマガジン (2021)。 URL: https://www.quantamagazine.org/mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/
https:/ / www.quantamagazine.org/ mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/

【6] フォルカー・ストラッセン。 「ガウス消去法は最適ではない」。 Numericsche Mathematik 13、354–356 (1969)。
https：/ / doi.org/ 10.1007 / BF02165411

【7] ケビン・スレーグル。 「量子ゲージ ネットワーク: 新しい種類のテンソル ネットワーク」。クォンタム 7、1113 (2023)。 arXiv:2210.12151。
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
arXiv：2210.12151

【8] ロマン・オルス。 「テンソル ネットワークへの実践的な入門: 行列積の状態と投影されたもつれペアの状態」。 Annals of Physics 349、117–158 (2014)。 arXiv:1306.2164。
https：/ / doi.org/ 10.1016 / j.aop.2014.06.013
arXiv：1306.2164

【9] マイケル・P・ザレテルとフランク・ポールマン。 「二次元におけるアイソメトリック テンソル ネットワーク状態」。 物理学。 レット牧師。 124、037201 (2020)。 arXiv:1902.05100。
https：/ / doi.org/ 10.1103 / PhysRevLett.124.037201
arXiv：1902.05100

【10] スティーブン・ワインバーグ。 「量子力学のテスト」。 『物理学年報』194、336–386 (1989)。
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

【11] N.ギシン。 「ワインバーグの非線形量子力学と超管腔通信」。 Physics Letters A 143、1–2 (1990)。
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

【12] ジョセフ・ポルチンスキー。 「ワインバーグの非線形量子力学とアインシュタイン・ポドルスキー・ローゼンのパラドックス」。物理学。レット牧師。 66、397–400 (1991)。
https：/ / doi.org/ 10.1103 / PhysRevLett.66.397

【13] ケビン・スレーグル。 「ノイズの多い量子コンピューターを使用した量子力学のテスト」(2021)。 arXiv:2108.02201。
arXiv：2108.02201

【14] ブライアン・スウィングル。 「時間順序がずれた相関関係子の物理学のスクランブルを解く」。 Nature Physics 14、988–990 (2018)。
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

【15] イグナシオ・ガルシア＝マタ、ロドルフォ・A・ハラベルト、ディエゴ・A・ウィズニアッキ。 「時間の順序が崩れた相関関係者と量子カオス」（2022年）。 arXiv:2209.07965。
arXiv：2209.07965

【16] ラーフル・ナンキショア氏とデビッド・A・ヒューズ氏。 「量子統計力学における多体局在化と熱化」。 Annual Review of Condensed Matter Physics 6、15–38 (2015)。 arXiv:1404.0686。
https：/ / doi.org/ 10.1146 / annurev-conmatphys-031214-014726
arXiv：1404.0686

【17] ドミトリー・A・アバニン、エフド・アルトマン、インマヌエル・ブロック、マクシム・セルビン。 「コロキウム: 多体局在化、熱化、およびもつれ」。 Modern Physics 91、021001 (2019) のレビュー。 arXiv:1804.11065。
https：/ / doi.org/ 10.1103 / RevModPhys.91.021001
arXiv：1804.11065

【18] ブルーノ・ナハターゲールとロバート・シムズ。 「何かについて大騒ぎ: リーブ・ロビンソン境界が役立つ理由」 (2011)。 arXiv:1102.0835。
arXiv：1102.0835

【19] ダニエル・A・ロバーツとブライアン・スウィングル。 「リーブ・ロビンソン結合と場の量子理論におけるバタフライ効果」。物理学。レット牧師。 117、091602 (2016)。 arXiv:1603.09298。
https：/ / doi.org/ 10.1103 / PhysRevLett.117.091602
arXiv：1603.09298

【20] Zhiyuan WangとKaden RA Hazzard。 「ローカルで相互作用するシステムにおけるリーブ・ロビンソンの束縛を強化する」。 PRX クォンタム 1、010303 (2020)。 arXiv:1908.03997。
https：/ / doi.org/ 10.1103 / PRXQuantum.1.010303
arXiv：1908.03997

によって引用

[1] Sayak Guha Roy と Kevin Slagle、「量子力学のゲージとシュレディンガー写真の間の補間」、 SciPost 物理コア 6 4、081 (2023).

[2] Kevin Slagle、「量子ゲージ ネットワーク: 新しい種類のテンソル ネットワーク」、 量子7、1113（2023）.

上記の引用は SAO / NASA ADS （最後に正常に更新された2024-03-22 22:55:39）。 すべての出版社が適切で完全な引用データを提供するわけではないため、リストは不完全な場合があります。

On Crossrefの被引用サービス 作品の引用に関するデータは見つかりませんでした（最後の試行2024-03-22 22:55:38）。

この論文は、 Creative Commons Attribution 4.0 International（CC BY 4.0） ライセンス。 著作権は、著者やその機関などの元の著作権者にあります。

タイムスタンプ：

より多くの 量子ジャーナル