極端な量子の正規直交基底

プラトン再発行

フォロワー： 0

マルシン・ルジンスキ^1,2, アダム・バーチャード³, KarolŻyczkowski^1,4

¹ヤギェウォ大学物理学、天文学および応用コンピュータサイエンス学部、ul。 Łojasiewicza11、30-348クラクフ、ポーランド
²ヤギェウォ大学、正確自然科学博士課程、UL。 Łojasiewicza 11, 30-348 クラクフ, ポーランド
³QuSoft、CWI およびアムステルダム大学、サイエンスパーク 123、1098 XG アムステルダム、オランダ
⁴理論科学センター、ポーランド科学アカデミー、Al。 Lotników32 / 46、02-668ワルシャワ、ポーランド

この論文を興味深いと思うか、議論したいですか？ SciRateを引用するかコメントを残す.

抽象

スピン反コヒーレント状態は、最も「量子的」な状態として最近多くの注目を集めています。いくつかのコヒーレントおよびアンチコヒーレントのスピン状態は、最適な量子ロトセンサーとして知られています。この研究では、個々のベクトルの平均反コヒーレンスとヴェールエントロピーによって決定される、スピン状態の正規直交基底の量子性の尺度を導入します。このようにして、最もコヒーレントで最も量子的な状態を特定し、それが極端な量子性の直交測定につながります。それらの対称性は、球上の点による純粋な状態の直観的な幾何学的表現を提供するマヨラナ恒星の表現を使用して明らかにすることができます。得られた結果は、$2j$ 量子ビットで構成される多部系の状態の $1^{2j}$ 次元空間の $2j+2$ 次元対称部分空間で最大 (最小) もつれ塩基を導き出しました。見つかった一部の塩基は、同じ程度のスピンコヒーレンスのすべての状態で構成されているため、アイソコヒーレントです。

極端な量子性の正規直交基底 PlatoBlockchain Data Intelligence。垂直検索。あい。

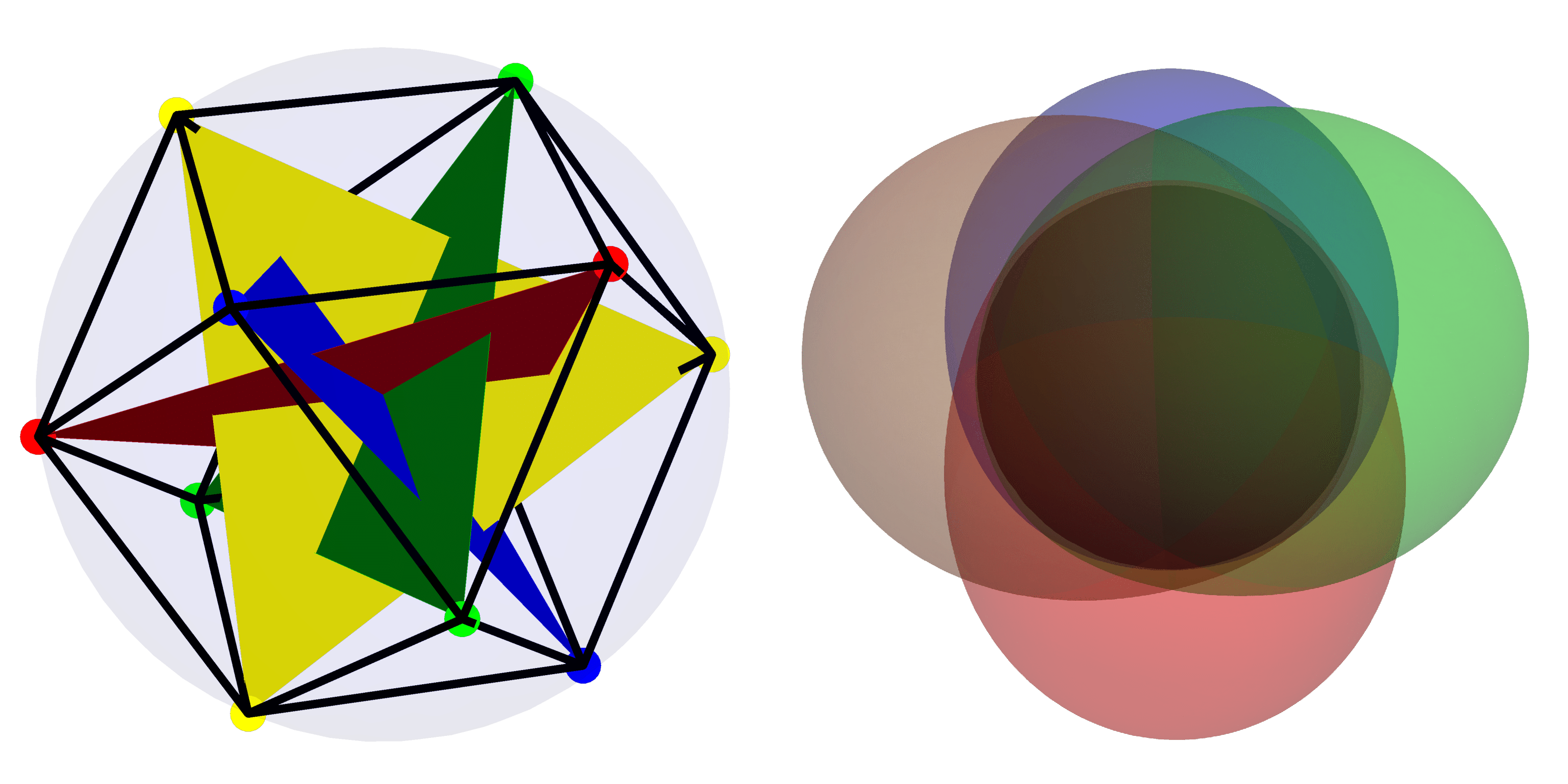
注目の画像: 左の画像では、$mathcal{H}_4$ の最も「量子」的な基底が恒星表現を使用して描かれています。右側には、$mathcal{H}_4$ 内の最も一貫した (「古典的」) 基底での状態の Husimi 関数が表示されます。

►BibTeXデータ

@article{Rudzinski2024orthonormalbasesof、doi = {10.22331/q-2024-01-25-1234}、url = {https://doi.org/10.22331/q-2024-01-25-1234}、title = {正規直交基底極端な量子性}、著者 = {Rudzi{'{n}}ski、Marcin と Burchardt、Adam と {.{Z}}yczkowski、Karol}、ジャーナル = {{Quantum}}、issn = {2521-327X}、出版社 = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}、ボリューム = {8}、ページ = {1234}、月 = 2024 月、年 = {XNUMX} }

►参照

【1] T. Frankel、『The Geometry of Physics: An Introduction』、第 3 版、Cambridge University Press (2011)。
https：/ / doi.org/ 10.1017 / CBO9781139061377

【2] D. Chruściński および A. Jamiołkowski、『古典力学および量子力学における幾何学的位相』、Birkhäuser (2004)。
https://doi.org/10.1007/978-0-8176-8176-0

【3] DA Lee、幾何相対性理論、アメリカ数学協会、プロビデンス (2021)。
https：/ / doi.org/ 10.1090 / gsm / 201

【4] I. Bengtsson、K. Życzkowski、『量子状態の幾何学: 量子もつれの概要』、第 2 版、ケンブリッジ大学出版局 (2017)。
https：/ / doi.org/ 10.1017 / 9781139207010

【5] M. Lewin、非線形多体量子システムの幾何学的手法、J. Functional Analysis 260、12、(2011)。
https：/ / doi.org/ 10.1016 / j.jfa.2010.11.017

【6] E. Cohen、H. Larocque、F. Bouchard 他、Aharonov-Bohm から Pancharatnam-Berry およびそれ以降の幾何学段階、Nat. Rev. Phys. 1、437–449 (2019)。
https://doi.org/10.1038/s42254-019-0071-1

【7] E. Majorana Atomi orientati in Campo Magneto Variable、Nuovo Cimento 9、43-50 (1932)。
https：/ / doi.org/ 10.1007 / BF02960953

【8] R. Barnett、A. Turner、および E. Demler、スピノール原子の新規相の分類、Phys.レット牧師。 97、180412 (2006)。
https：/ / doi.org/ 10.1103 / PhysRevLett.97.180412

【9] R. Barnett、A. Turner、および E. Demler、 $S=3$ ボースアインシュタイン凝縮における渦の分類、Phys. Rev. A 76、013605 (2007)。
https：/ / doi.org/ 10.1103 / PhysRevA.76.013605

【10] H. マケラ、K.-A.スオミネン、スピン系の不活性状態、物理学。レット牧師。 99、190408 (2007)。
https：/ / doi.org/ 10.1103 / PhysRevLett.99.190408

【11] E. Serrano-Ensástiga、および F. Mireles、スピノルボースアインシュタイン凝縮体の位相特性評価: マヨラナ星表現アプローチ、Phys.レット。 A 492、129188 (2023)。
https：/ / doi.org/ 10.1016 / j.physleta.2023.129188

【12] P. Mathonet 他、$N$-qubit 対称状態のもつれ等価性、Phys. Rev. A 81、052315 (2010)。
https：/ / doi.org/ 10.1103 / PhysRevA.81.052315

【13] J. Martin、O. Giraud、PA Braun、D. Braun、および T. Bastin、高度な幾何学的もつれを伴う Multiqubit 対称状態、Phys. Rev. A 81、062347 (2010)。
https：/ / doi.org/ 10.1103 / PhysRevA.81.062347

【14] M. Aulbach、DJH Markham、および M. Murao、幾何学的尺度に関する最大限にもつれた対称状態、New J. Phys. 12、073025 (2010)。
https://doi.org/10.1088/1367-2630/12/7/073025

【15] DJH Markham、順列対称状態におけるもつれと対称性、Phys. Rev. A 83、042332 (2011)。
https：/ / doi.org/ 10.1103 / PhysRevA.83.042332

【16] P. Ribeiro、R. Mosseri、$n$ qubits の対称セクターにおけるもつれ、Phys.レット牧師。 106、180502 (2011)。
https：/ / doi.org/ 10.1103 / PhysRevLett.106.180502

【17] M.Aulbach、対称状態におけるもつれの分類、Int. J.クォンタム・インフォーム。 10、1230004 (2012)。
https：/ / doi.org/ 10.1142 / S0219749912300045

【18] W. Ganczarek、M. Kuś、および K. Życzkowski、量子もつれの重心測定、Phys. Rev. A 85、032314 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevA.85.032314

【19] A. Mandilara、T. Coudreau、A. Keller、および P. Milman、スピンコヒーレント状態による純粋対称状態のもつれ分類、Phys. Rev. A 90、050302(R) (2014)。
https：/ / doi.org/ 10.1103 / PhysRevA.90.050302

【20] Ｐ．Ｈｙｌｌｕｓら、フィッシャー情報と多粒子エンタングルメント、Ｐｈｙｓ． Rev. A 85、022321 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevA.85.022321

【21] JH Hannay、マヨラナ表現におけるスピンのベリー相、J. Phys. A: 数学です。 Gen. 31、L53 (1998)。
https://doi.org/10.1088/0305-4470/31/2/002

【22] Ｐ．ブルーノ、マヨラナの恒星表現における量子幾何学的位相：多体アハロノフ・ボーム位相へのマッピング、Ｐｈｙｓ．レット牧師。 108、240402 (2012)。
https：/ / doi.org/ 10.1103 / PhysRevLett.108.240402

【23] HD Liu、LB Fu、マヨラナの恒星表現におけるベリーの位相と量子もつれ、物理学。 Rev. A 94、022123 (2016)。
https：/ / doi.org/ 10.1103 / PhysRevA.94.022123

【24] P. Ribeiro、J. Vidal、および R. Mosseri、Lipkin-Meshkov-Glick モデルの熱力学的限界、Phys.レット牧師。 99、050402 (2007)。
https：/ / doi.org/ 10.1103 / PhysRevLett.99.050402

【25] P. Ribeiro、J. Vidal、および R. Mosseri、熱力学限界および有限サイズ補正におけるリプキン・メシュコフ・グリックモデルの正確なスペクトル、Phys. Rev. E 78、021106 (2008)。
https：/ / doi.org/ 10.1103 / PhysRevE.78.021106

【26] J. Zimba、マヨラナ表現による「反コヒーレント」スピン状態、Electron。Ｊ．Ｔｈｅｏｒ．物理学。 3、143 (2006)。
https:/ / api.semanticscholar.org/ CorpusID:13938120

【27] D.バゲット、T。バスティン、およびJ.マーティン、最大限に混合された90キュービット削減を伴うマルチキュービット対称状態、Phys。 Rev. A 032314、2014（XNUMX）。
https：/ / doi.org/ 10.1103 / PhysRevA.90.032314

【28] O.ジロー、D。ブラウン、D。バゲット、T。バスティン、J。マーティン、スピン状態のテンソル表現、Phys。レット牧師。 114、080401（2015）。
https：/ / doi.org/ 10.1103 / PhysRevLett.114.080401

【29] D.バゲット、F。ダマネ、O。ジロー、およびJ.マーティン、点群対称性を持つスピン状態の反干渉性、Phys。 Rev. A 92、052333（2015）。
https：/ / doi.org/ 10.1103 / PhysRevA.92.052333

【30] HD Liu、LB Fu、X. Wang、マヨラナ表現のためのコヒーレント状態アプローチ、Commun。理論。物理学。 67、611 (2017)。
https://doi.org/10.1088/0253-6102/67/6/611

【31] D. Baguette および J. Martin、純粋なスピン状態の反コヒーレンス測定、Phys. Rev. A 96、032304 (2017)。
https：/ / doi.org/ 10.1103 / PhysRevA.96.032304

【32] P. Kolenderski、R. Demkowicz-Dobrzański、参照フレームの位置合わせとプラトン立体を維持するための最適な状態、Phys. Rev. A 78、052333 (2008)。
https：/ / doi.org/ 10.1103 / PhysRevA.78.052333

【33] C. Chryssomalakos、および H. Hernandez-Coronado、最適量子ロトセンサー、Phys. Rev. A 95、052125 (2017)。
https：/ / doi.org/ 10.1103 / PhysRevA.95.052125

【34] AZ Goldberg および DFV James、反コヒーレント状態を使用した量子限定オイラー角測定、Phys. Rev. A 98、032113 (2018)。
https：/ / doi.org/ 10.1103 / PhysRevA.98.032113

【35] J. Martin、S. Weigert、および O. Giraud、コヒーレントおよび反コヒーレント状態による未知の軸を中心とした回転の最適検出、Quantum 4、285 (2020)。
https://doi.org/10.22331/q-2020-06-22-285

【36] J. Crann、DW Kribs、および R. Pereira、球面設計と反コヒーレントスピン状態、J. Phys. A: 数学です。理論。 43、255307 (2010)。
https://doi.org/10.1088/1751-8113/43/25/255307

【37] E. Bannai および M. Tagami、反コヒーレントスピン状態に関するメモ、J. Phys. A: 数学です。理論。 44、342002 (2011)。
https://doi.org/10.1088/1751-8113/44/34/342002

【38] M. Wang および Y. Zhu、反コヒーレントスピン 2 状態と球状デザイン、J. Phys. A: 数学です。理論。 55、425304 (2022)。
https:/ / doi.org/ 10.1088/ 1751-8121/ ac971d

【39] AZ Goldberg、AB Klimov、M.Grassl、G. Leuchs、および LL Sánchez-Soto、極限量子状態、AVS Quantum Sci. 2、044701 (2020)。
https：/ / doi.org/ 10.1116 / 5.0025819

【40] AZ Goldberg、M. Grassl、G. Leuchs、および LL Sánchez-Soto、もつれを超えた量子性: 対称状態の場合、Phys. Rev. A 105、022433 (2022)。
https：/ / doi.org/ 10.1103 / PhysRevA.105.022433

【41] O. Giraud、P. Braun、および D. Braun、Quantifying quantumness and the Quest for Queens of Quantum、New J. Phys. 12、063005 (2010)。
https://doi.org/10.1088/1367-2630/12/6/063005

【42] R. Delbourgo、回転グループと関連グループの最小不確実性状態、J. Phys. A 10、L233 (1977)。
https://doi.org/10.1088/0305-4470/10/11/012

【43] A. Wehrl、古典的エントロピーと量子力学的エントロピーの関係について、議員 Math。物理学。 16、353 (1979)。
https://doi.org/10.1016/0034-4877(79)90070-3

【44] EH Lieb、Wehrl のエントロピー予想の証明、Commun。数学。物理学。 62、35 (1978)。
https：/ / doi.org/ 10.1007 / BF01940328

【45] CT Lee、Wehrl のスピン状態のエントロピーと Lieb の予想、J. Phys. A 21、3749 (1988)。
https://doi.org/10.1088/0305-4470/21/19/013

【46] EH Lieb、JP Solovej、ブロッホコヒーレントスピン状態のエントロピー予想とその一般化の証明、Acta Math。 212、379 (2014)。
https://doi.org/10.1007/s11511-014-0113-6

【47] F. Bouchard ら、極値マヨラナ星座による限界の量子計測学、Optica 4、1429-1432 (2017)。
https：/ / doi.org/ 10.1364 / OPTICA.4.001429

【48] A. Wehrl、エントロピーの一般特性、Rev. Mod.物理学。 50、221 (1978)。
https：/ / doi.org/ 10.1103 / RevModPhys.50.221

【49] A. Wehrl、エントロピーのさまざまな側面、数学議員。物理学。 30、119 (1991)。
https://doi.org/10.1016/0034-4877(91)90045-O

【50] S. Gnutzmann および K. Życzkowski、位相空間における局在化の尺度としての Renyi-Wehrl エントロピー、J. Phys. A 34、10123 (2001)。
https://doi.org/10.1088/0305-4470/34/47/317

【51] K. Życzkowski、固有状態の局在化と平均ヴェールエントロピー、Physica E 9、583 (2001)。
https://doi.org/10.1016/S1386-9477(00)00266-6

【52] LL Sánchez-Soto、AB Klimov、P. de la Hoz、および G. Leuchs、量子対古典偏光状態: 多極子が考慮されるとき、J. Phys. B 46 104011 (2013)。
https://doi.org/10.1088/0953-4075/46/10/104011

【53] A. Tavakoli、および N. Gisin、「プラトン固体と量子力学の基礎テスト」、Quantum 4、293 (2020)。
https://doi.org/10.22331/q-2020-07-09-293

【54] H.C. Nguyen、S. Designolle、M. Barakat、および O. Gühne、量子力学における測定間の対称性、プレプリント arXiv:2003.12553 (2022)。
https：/ / doi.org/ 10.48550 / arXiv.2003.12553
arXiv：2003.12553

【55] JI Latorre、G. Sierra、プラトンもつれ、量子研究所計算します。 21、1081 (2021)。
https：/ / doi.org/ 10.26421 / QIC21.13-14-1

【56] K. Bolonek-Lasoń、および P. Kosiński、群、プラトン立体およびベル不等式、Quantum 5、593 (2021)。
https://doi.org/10.22331/q-2021-11-29-593

【57] KF Pál、T. Vértesi、グループ、すべての次元のプラトニックベル不等式、Quantum 6、756 (2022)。
https://doi.org/10.22331/q-2022-07-07-756

【58] RH Dicke、自然放射線プロセスにおけるコヒーレンス、Phys.改訂 93、99 (1954)。
https：/ / doi.org/ 10.1103 / PhysRev.93.99

【59] V. カリミプール、および L. メマルザデ、任意の次元における等交絡合塩基 Phys. Rev. A 73、012329 (2006)。
https：/ / doi.org/ 10.1103 / PhysRevA.73.012329

【60] G. Rajchel、A. Gąsiorowski、および K. Życzkowski、ロバストアダマール行列、バーコフ多面体における非確率光線、および複合空間における等量もつれ基底。コンプ。科学。 12、473 (2018)。
https：/ / doi.org/ 10.1007 / s11786-018-0384-y

【61] J. Czartowski、D. Goyeneche、M. Grassl、および K. Życzkowski、Isoentangled相互不偏塩基、対称量子測定、および混合状態設計、Phys.レット牧師。 124、090503 (2020)。
https：/ / doi.org/ 10.1103 / PhysRevLett.124.090503

【62] F. Del Santo、J. Czartowski、K. Życzkowski、および N. Gisin、Iso-entangled Base and Joint Measurements、プレプリント arXiv:2307.06998 (2023)。
https：/ / doi.org/ 10.48550 / arXiv.2307.06998
arXiv：2307.06998

【63] R. ペンローズ、「確率のないベルの非局所性: いくつかの奇妙な幾何学」、量子反射 (2000)。

【64] J. ジンバと R. ペンローズ、確率のないベルの非局所性: より興味深い幾何学、スタッド。履歴。フィル。科学。 24、697 (1993)。
https://doi.org/10.1016/0039-3681(93)90061-N

【65] JE Massad、PK Aravind、ペンローズ十二面体再考、Am。 J. Physics 67、631 (1999)。
https：/ / doi.org/ 10.1119 / 1.19336

【66] K. Husimi、密度行列のいくつかの形式的特性、Proc.物理学。数学。社会22、264 (1940)。
https：/ / doi.org/ 10.11429 / ppmsj1919.22.4_264

【67] W. Słomczyński、および K. Życzkowski、球上の量子マップの平均動的エントロピーは半古典限界で発散、Phys.レット牧師。 80、1880 (1998)。
https：/ / doi.org/ 10.1103 / PhysRevLett.80.1880

【68] M. Piotrak、M. Kopciuch、AD Fard、M. Smolis、S. Pustelny、K. Korzekwa、完全量子分度器、プレプリント arXiv:2310.13045 (2023)。
https：/ / doi.org/ 10.48550 / arXiv.2310.13045
arXiv：2310.13045

【69] NCN Maestro 7 2015/ 18/ A/ ST2/ 00274 ウェブサイト https:/ / chaos.if.uj.edu.pl/ karol/ Maestro7/ files/ data3/ Numerical_Results.dat。
https:/ / chaos.if.uj.edu.pl/~karol/Maestro7/files/data3/Numerical_Results.dat

【70] D. Weingarten、無限ランクの極限における群積分の漸近挙動、J. Math.物理学。 19, 999 (1978)。
https：/ / doi.org/ 10.1063 / 1.523807

【71] B. Collins、および P. Śniady、Integration with Respect to the Haar Measure on Unitary, Orthogonal and symplectic group、Commun。数学。物理学。 264、773 (2006)。
https://doi.org/10.1007/s00220-006-1554-3

【72] G. Rajchel、量子マッピングと設計、博士論文、プレプリント arXiv:2204.13008 (2022)。
https：/ / doi.org/ 10.48550 / arXiv.2204.13008
arXiv：2204.13008

【73] D. Martin、EP Wigner、群理論と原子スペクトルの量子力学への応用、Academic Press Inc. NY (1959)。
https://doi.org/10.1016/b978-0-12-750550-3.x5001-0

によって引用

[1] Michał Piotrak、Marek Kopciuch、Arash Dezhang Fard、Magdalena Smolis、Szymon Pustelny、Kamil Korzekwa、「完璧な量子分度器」、 arXiv：2310.13045, (2023).

[2] アーロン Z. ゴールドバーグ、「対称状態にある粒子のサブセットの相関: 残りが無視されたときに光子が光線内で何をしているか」、 arXiv：2401.05484, (2024).

上記の引用は SAO / NASA ADS （最後に正常に更新された2024-01-25 23:58:21）。すべての出版社が適切で完全な引用データを提供するわけではないため、リストは不完全な場合があります。

On Crossrefの被引用サービス作品の引用に関するデータは見つかりませんでした（最後の試行2024-01-25 23:58:19）。

この論文は、 Creative Commons Attribution 4.0 International（CC BY 4.0）ライセンス。著作権は、著者やその機関などの元の著作権者にあります。

SEO を活用したコンテンツと PR 配信。今日増幅されます。
PlatoData.Network 垂直生成 Ai。自分自身に力を与えましょう。こちらからアクセスしてください。
プラトアイストリーム。 Web3 インテリジェンス。知識増幅。こちらからアクセスしてください。
プラトンESG。カーボン、クリーンテック、エネルギー、環境、太陽、廃棄物管理。こちらからアクセスしてください。
プラトンヘルス。バイオテクノロジーと臨床試験のインテリジェンス。こちらからアクセスしてください。
情報源： https://quantum-journal.org/papers/q-2024-01-25-1234/

タイムスタンプ： 2024 年 1 月 25 日

タイムスタンプ： 2024 年 1 月 24 日

極端な量子性の正規直交基底

プラトン再発行

抽象

人気の要約

►BibTeXデータ

►参照

によって引用

より多くの量子ジャーナル

SU(N) の登場: 多変量量子ゲートと勾配

トポロジカルフォールトトレラントな量子誤り訂正のための連結スキーム

アプリケーションを使用した時空効率の高い低深度量子状態の準備

qBang を使用した変分量子アルゴリズムの最適化: メトリックとモメンタムを効率的に織り交ぜてフラットエネルギーランドスケープをナビゲートする

自由電子の量子論理ゲート

ハミルトニアンシミュレーション用の並列量子アルゴリズム

Reqomp: 量子回路のためのスペース制約のある非計算

時間最適化マルチキュービットゲートの合成とコンパイル

量子LDPC符号と反復復号によるもつれの浄化

私たちに関しては

垂直検索とAi

プラットフォーム

フォロー

抽象

によって引用

より多くの 量子ジャーナル

私たちに関しては

垂直検索とAi

プラットフォーム

フォロー

より多くの量子ジャーナル