1ICFO-Institut de Ciencies Fotoniques、バルセロナ科学技術研究所、08860 Castelldefels、スペイン
2CFIS-Centre de Formació Interdisciplinària Superior、UPC-Universitat Politècnica de Catalunya、08028 バルセロナ、スペイン
3Univ Grenoble Alpes、CNRS、Grenoble INP、Institut Néel、38000 グルノーブル、フランス
4ICREA-Institucio Catalana de RecercaiEstudisAvançats、Lluis Company 23、08010バルセロナ、スペイン
この論文を興味深いと思うか、議論したいですか? SciRateを引用するかコメントを残す.
抽象
相互に偏りのない基底は、量子情報理論における非常に有用な測定値のペアに対応します。 最小の複合次元である 2 では、相互に偏りのない基底が 83 ~ 062303 個存在することが知られており、Zauner の予想として知られる数十年前の予想では、存在するのは最大 2011 個であるとされています。 ここでは、$n$ MUB がその次元に存在する場合に限り、次元 $d$ で最大に破ることができる整数 $n,d ge XNUMX$ のすべてのペアに対するベルの不等式の構築を通じて、Zauner の予想に数値的に取り組みます。 したがって、Zauner の予想を最適化問題に変換し、シーソー最適化、非線形半正定値計画法、モンテカルロ法という XNUMX つの数値手法を使用して解決します。 XNUMX つの方法はすべて、低次元の既知のケースを正しく識別し、XNUMX 次元には相互に偏りのない XNUMX つの基底が存在しないことを示唆しており、対応するベルの不等式を数値的に最適化する同じ基底をすべて見つけています。 さらに、これらの数値オプティマイザーは、[P. Raynal, X. Lü, B.-G. エングラート、{Phys. Rev. A}、{ XNUMX} XNUMX (XNUMX)]。 最後に、モンテカルロの結果は、最大で XNUMX つの MUB が次元 XNUMX に存在することを示唆しています。
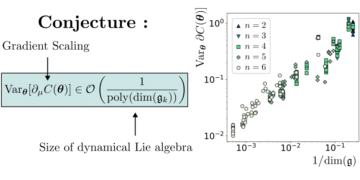
主な画像: 次元 d に n 個の MUB が存在すると仮定した場合のベルの不等式の値と、数値的手法によって検出された値との相対的な差。 ゼロの値は、メソッドが次元 d で n 個の MUB を検出したことを意味し、ゼロ以外の値は、メソッドが次元 d で n 個の MUB を検出しなかったことを意味します。 既知のすべてのケース (次元 XNUMX から XNUMX および XNUMX と XNUMX の MUB を含む次元 XNUMX) は、数値によって正しく識別されます。 次元 XNUMX では、どのメソッドも XNUMX つの MUB を見つけられず、すべてのメソッドが XNUMX つの塩基の同じセットに収束します。
人気の要約
幅広い用途にもかかわらず、MUB の構造に関して未解決の問題が残っています。 最も顕著なのは、量子系の次元が合成数である場合、ペアワイズで偏りのない測定値の最大数 (「MUB の数」) が不明であることです。 特に、次元 XNUMX では、MUB の数が XNUMX から XNUMX の間であることがわかっています。 XNUMX 次元には XNUMX つ以下の MUB しか存在しないという、ザウナーの長年にわたる未解決の予想があります。 この数十年にわたる推測は、いくつかの数値的証拠によって裏付けられていますが、今日まで証拠はありません。
この作業では、ベルの非局所性を通じてザウナーの予想に取り組みます。 ベルの非局所性は、通信を許可されていないが、古典的なランダム性または共有量子状態の形でいくつかの相関関係を共有できる XNUMX 人の実験者に関係しています。 量子リソースを共有すると、古典物理学 (より正確には、いわゆる局所隠れ変数モデル) では説明できない実験データが得られる可能性があることが示されています。 これはベルの定理として知られており、過去 XNUMX 年間で実験的に検証されています。 実験データの非古典性を目の当たりにすることは、実験で発生する測定結果の確率の関数である、いわゆるベルの不等式を介して最も一般的に行われます。 古典的なデータはベルの不等式を満たさなければなりませんが、量子データはベルの不等式に違反する可能性があります。
最近、当事者の XNUMX 人が特定の次元の MUB 測定値のペアを使用すると、ベルの不等式が最大限に破られることがわかりました。 この作業では、これらの不等式を新しい不等式に拡張し、特定の次元で選択された数の MUB 測定値によって最大限に侵害されます。 さらに、実験の次元が固定されている場合、採用された測定値が特定の次元で選択された MUB の数に対応する場合にのみ、最大の違反が得られます。 したがって、選択した数の MUB が特定の次元に存在するかどうかを判断することは、この固定次元で対応するベルの不等式の最大違反を見つけることと同じです。
この最大の違反を見つけることは一般に困難な問題ですが、固定次元でのベルの不等式の最大の違反を見つける試みとして、XNUMX つの異なる数値手法を使用します。 これらの方法のうちの XNUMX つは半正定値計画法手法の変形であり、XNUMX つ目の方法は統計物理学に着想を得たもので、シミュレーテッド アニーリングと呼ばれます。 これらの方法はすべてヒューリスティックです (つまり、問題の真の最適解が見つかるという保証はありません) が、最適解がわかっている最適化問題に適用することで、そのパフォーマンスを測定できます。 特に、XNUMX つの方法のすべてが、MUB 測定値が存在することがわかっている場合に、それらを正しく識別できることがわかりました。 さらに、それらが存在しないことがわかっている場合、XNUMX つの方法はすべて、数値精度まで同じ測定セットに収束します。 次に、最初の未知のケース、つまり次元 XNUMX の XNUMX つの MUB にメソッドを適用します。 いずれの方法も次元 XNUMX で XNUMX つの MUB を識別できませんが、数値精度まで XNUMX つの測定値の同じセットにすべて収束します。 さらに、シミュレーテッド アニーリング手法では、次の複合次元である次元 XNUMX に XNUMX つの MUB が見つかりません。 したがって、私たちの手法のヒューリスティックな性質のために厳密な主張を行うことはできませんが、私たちの結果は、ベルの非局所性の新しい観点からザウナーの予想を支持しています。
►BibTeXデータ
►参照
【1] IDイバノビッチ。 量子状態決定の幾何学的記述。 Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/ 0305-4470/ 14/ 12/ 019.
https://doi.org/10.1088/0305-4470/14/12/019
【2] G.ブラサードCHベネット。 量子暗号: 公開鍵の配布とコイン投げ。 IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/ j.tcs.2011.08.039.
https:/ / doi.org/ 10.1016 / j.tcs.2011.08.039
【3] アルトゥール・K・エケルト。 ベルの定理に基づく量子暗号。 物理。 Rev. Lett., 67:661–663, 1991. doi:10.1103/ PhysRevLett.67.661.
https:/ / doi.org/ 10.1103 / PhysRevLett.67.661
【4] ダグマー・ブルス。 81 つの状態を持つ量子暗号における最適な盗聴。 物理。 Rev. Lett., 3018:3021–1998, 10.1103. doi:81.3018/ PhysRevLett.XNUMX.
https:/ / doi.org/ 10.1103 / PhysRevLett.81.3018
【5] アーミン・タヴァコリ、アレイ・ハメディ、ブレノ・マルケス、モハメド・ブーレンナン。 単一の $d$ レベル システムを使用した量子ランダム アクセス コード。 物理。 Rev. Lett., 114:170502, 2015. doi:10.1103/ PhysRevLett.114.170502.
https:/ / doi.org/ 10.1103 / PhysRevLett.114.170502
【6] マテ・ファルカスとイェンジェイ・カニエフスキー。 準備と測定のシナリオで、相互に偏りのないベースを自己テストします。 物理。 Rev. A, 99:032316, 2019. doi:10.1103/ PhysRevA.99.032316.
https:/ / doi.org/ 10.1103 / PhysRevA.99.032316
【7] H. Bechmann-Pasquinucci と N. Gisin。 バイナリ測定による量子単位のベルの不等式。 量子情報。 Comput., 3(2):157–164, 2003. doi:10.26421/ QIC3.2-6.
https:/ / doi.org/ 10.26421 / QIC3.2-6
【8] Jędrzej Kaniewski、Ivan Šupić、Jordi Tura、Flavio Baccari、Alexia Salavrakos、および Remigiusz Augusiak。 最大のエンタングルメントと相互に偏りのないベースによる最大の非局所性、および 3 クォートリット量子システムの自己テスト。 量子、198:2019、10.22331. doi:2019/ q-10-24-198-XNUMX.
https://doi.org/10.22331/q-2019-10-24-198
【9] Armin Tavakoli、Máté Farkas、Denis Rosset、Jean-Daniel Bancal、および Jędrzej Kaniewski。 ベル実験では、相互に偏りのないベースと対称的な情報の完全な測定が行われます。 Science Advances, 7(7):eabc3847, 2021. doi:10.1126/ sciadv.abc3847.
https:/ / doi.org/ 10.1126/ sciadv.abc3847
【10] Thomas Durt、Berthold-Georg Englert、Ingemar Bengtsson、Karol Życzkowski。 相互に公平な基準で。 量子情報の国際ジャーナル、08(04):535–640、2010 年。
https:/ / doi.org/ 10.1142 / S0219749910006502
【11] ウィリアム・K・ウーターズとブライアン・D・フィールズ。 相互に偏りのない測定による最適な状態決定。 年報, 191(2):363–381, 1989. doi:10.1016/ 0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
【12] Paweł Wocjan と Thomas Beth。 正方形の次元で相互に偏りのないベースの新しい構築。 量子情報。 Comput., 5(2):93–101, 2005. doi:10.26421/ QIC5.2-1.
https:/ / doi.org/ 10.26421 / QIC5.2-1
【13] ミハイ・ワイナー。 相互に偏りのない塩基の最大数のギャップ。 議事録アメール。 算数。 Soc., 141:1963–1969, 2013. doi:10.1090/ S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
【14] ゲルハルト・ザウナー。 Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. 博士論文、1999 年。
【15] P.オスカー・ボイキン、ミーラ・シタラム、ファム・フー・ティエプ、パウエル・ウォッジャン。 リー代数の相互に偏りのない基底と直交分解。 量子情報。 Comput., 7(4):371–382, 2007. doi:10.26421/ QIC7.4-6.
https:/ / doi.org/ 10.26421 / QIC7.4-6
【16] Stephen Brierley と Stefan Weigert。 次元 79 で相互に偏りのないベースを構築します。 物理。 Rev. A、052316:2009、10.1103 年。doi:79.052316/ PhysRevA.XNUMX。
https:/ / doi.org/ 10.1103 / PhysRevA.79.052316
【17] Philippe Jaming、Máté Matolcsi、Péter Móra、Ferenc Szöllősi、および Mihály Weiner。 一般化されたパウリ問題と 6 次元の MUB トリプレットの無限族. Journal of Physics A: Mathematical and Theoretical、42(24):245305、2009 年 10.1088 月. doi:1751/ 8113-42/ 24/ 245305/ XNUMX.
https://doi.org/10.1088/1751-8113/42/24/245305
【18] ゲイリー・マコーネル、ハリー・スペンサー、アファク・タヒール。 $mathbb{C}^6$ の Zauner の MUB 予想に対する支持と反対の証拠。 2021. doi:10.48550/ arXiv.2103.08703.
https:/ / doi.org/ 10.48550 / arXiv.2103.08703
【19] サンダー・グリブリングとスヴェン・ポラック。 相互に偏りのない基底: 多項式の最適化と対称性。 2021. doi:10.48550/ arXiv.2111.05698.
https:/ / doi.org/ 10.48550 / arXiv.2111.05698
【20] Ingemar Bengtsson、Wojciech Bruzda、Åsa Ericsson、Jan-Åke Larsson、Wojciech Tadej、Karol Życzkowski。 相互に偏りのない基底と 48 次のアダマール行列。 Journal of Mathematical Physics, 5(052106):2007, 10.1063. doi:1.2716990/ XNUMX.
https:/ / doi.org/ 10.1063 / 1.2716990
【21] Philippe Raynal、Xin Lü、Berthold-Georg Englert。 83 次元で相互に偏りのない塩基: 最も離れた 062303 つの塩基。 物理。 Rev. A, 2011:10.1103, 83.062303. doi:XNUMX/ PhysRevA.XNUMX.
https:/ / doi.org/ 10.1103 / PhysRevA.83.062303
【22] Edgar A. Aguilar、Jakub J. Borkała、Piotr Mironowicz、Marcin Pawłowski。 相互に偏りのない塩基と量子ランダム アクセス コードの間の接続。 物理。 Rev. Lett., 121:050501, 2018. doi:10.1103/ PhysRevLett.121.050501.
https:/ / doi.org/ 10.1103 / PhysRevLett.121.050501
【23] ニコラス・ブルナー、ダニエル・カヴァルカンティ、ステファノ・ピロニオ、バレリオ・スカラニ、ステファニー・ヴェーナー。 ベルの非局所性。 牧師Mod。 Phys。、86:419–478、2014年。doi:10.1103 /RevModPhys.86.419。
https:/ / doi.org/ 10.1103 / RevModPhys.86.419
【24] MOSEK ApS. C++ 9.2.49 用の MOSEK Fusion API、2021。URL: https:/ / docs.mosek.com/ 9.2/ cxxfusion/ index.html。
https:/ / docs.mosek.com/ 9.2/ cxxfusion/ index.html
【25] 山下ヒロシ、矢部浩史、原田耕平。 非線形半定値計画法のための主双対内点法。 数学プログラミング、135(1):89–121、2012 年。
https:/ / doi.org/ 10.1007 / s10107-011-0449-z
【26] Stephen Boyd and Lieven Vandenberghe.スティーブンボイドとリーヴェンヴァンデンベルグ。 Convex Optimization.凸最適化。 Cambridge University Press, 2004. doi:10.1017/CBO9780511804441.ケンブリッジ大学出版局、XNUMX年。doi:XNUMX / CBOXNUMX。
https:/ / doi.org/ 10.1017 / CBO9780511804441
【27] S. Kirkpatrick、CD Gelatt、および MP Vecchi。 シミュレーテッド・アニーリングによる最適化。 Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https:/ / doi.org/ 10.1126 / science.220.4598.671
【28] ニコラス・メトロポリス、アリアナ・W・ローゼンブルース、マーシャル・N・ローゼンブルース、オーガスタ・H・テラー、エドワード・テラー。 高速計算機による状態方程式計算。 ジャーナル オブ ケミカル フィジックス、21(6):1087–1092、1953。doi:10.1063/ 1.1699114。
https:/ / doi.org/ 10.1063 / 1.1699114
【29] ミゲル・ナバスケス、ステファノ・ピロニオ、アントニオ・アシン。 量子相関のセットの境界。 物理。 Rev. Lett., 98:010401, 2007. doi:10.1103/ PhysRevLett.98.010401.
https:/ / doi.org/ 10.1103 / PhysRevLett.98.010401
によって引用
この論文は、 Creative Commons Attribution 4.0 International(CC BY 4.0) ライセンス。 著作権は、著者やその機関などの元の著作権者にあります。