극단적인 양자성의 직교 기초

극단적인 양자성의 직교 기초

타임 스탬프 : 25 년 2024 월 6 일 오전 51:XNUMX

마르신 루진스키1,2, 아담 버차트3및 카롤 지츠코프스키1,4

1물리, 천문학 및 응용 컴퓨터 과학 학부, Jagiellonian University, ul. Łojasiewicza 11, 30-348 크라쿠프, 폴란드
2Jagiellonian University, ul.의 정밀 및 자연 과학 박사 과정. Łojasiewicza 11, 30-348 크라쿠프, 폴란드
3QuSoft, CWI 및 University of Amsterdam, Science Park 123, 1098 XG Amsterdam, 네덜란드
4폴란드 과학 아카데미 이론 물리학 센터, Al. Lotników 32/46, 02-668 바르샤바, 폴란드

이 논문이 흥미 롭거나 토론하고 싶습니까? SciRate에 댓글을 달거나 댓글 남기기.

추상

스핀 역간섭 상태는 최근 가장 "양자" 상태로서 많은 주목을 받았습니다. 일부 응집성 및 반대성 스핀 상태는 최적의 양자 로토센서로 알려져 있습니다. 이 연구에서는 개별 벡터의 평균 역간섭과 Wehrl 엔트로피에 의해 결정되는 스핀 상태의 정규 직교 기반에 대한 양자성 척도를 소개합니다. 이러한 방식으로 우리는 가장 일관되고 가장 양자적인 상태를 식별하여 극단적인 양자성의 직교 측정으로 이어집니다. 이들의 대칭성은 구 위의 점을 통해 순수한 상태를 직관적인 기하학적 표현으로 제공하는 마요라나(Majorana) 항성 표현을 사용하여 드러날 수 있습니다. 얻은 결과는 $2j$ 큐비트로 구성된 다중 부분 시스템 상태의 $1^{2j}$ 차원 공간의 $2j+2$ 차원 대칭 하위 공간에서 최대(최소) 얽힌 베이스로 이어집니다. 발견된 일부 염기는 동일한 수준의 스핀 일관성을 갖는 모든 상태로 구성되므로 등간섭성입니다.

극도의 양자성 PlatoBlockchain 데이터 인텔리전스의 직교 정규 기반. 수직 검색. 일체 포함.

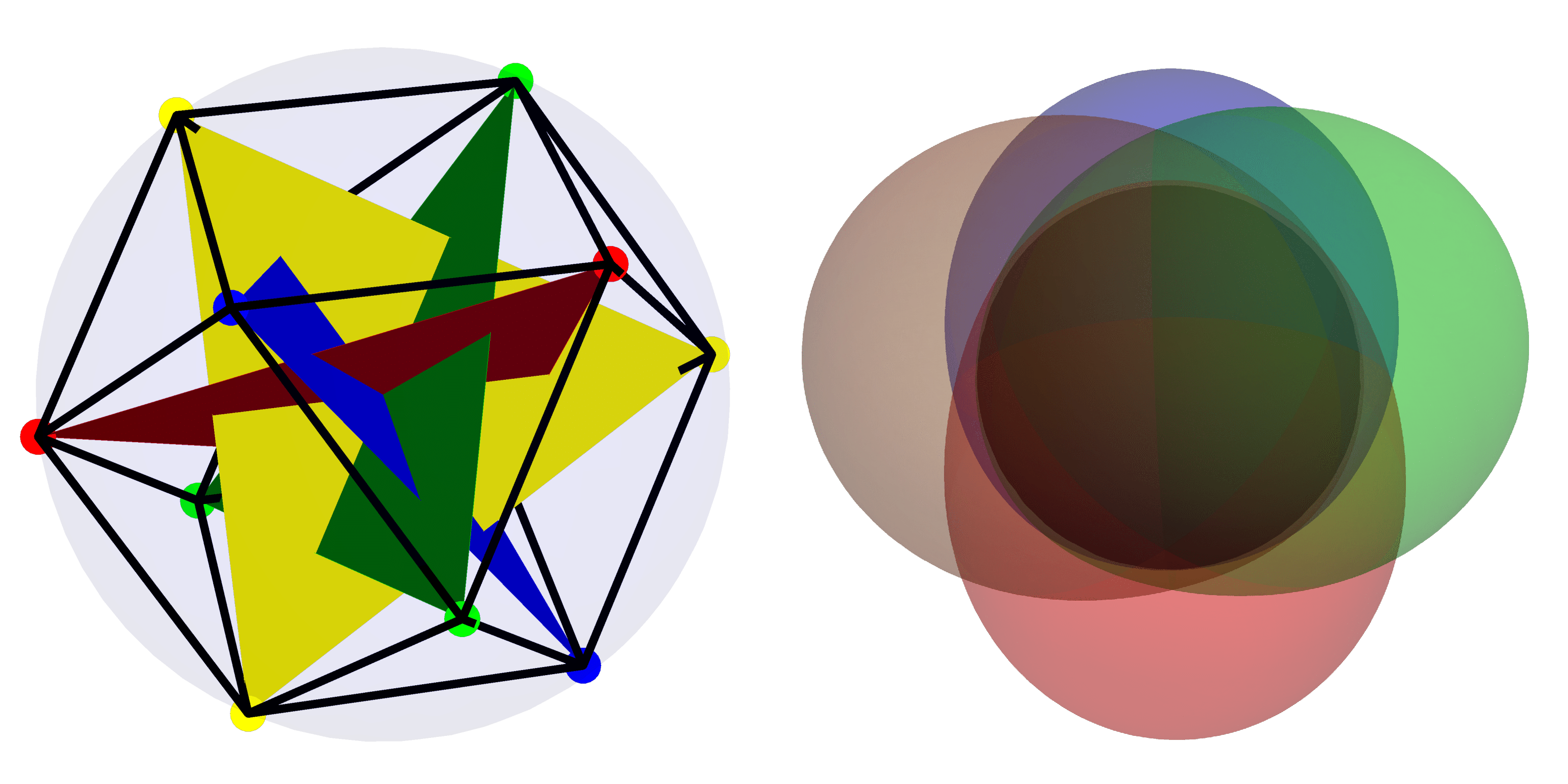
주요 이미지: 왼쪽 이미지에서는 $mathcal{H}_4$의 가장 "양자" 기반이 별 표현을 사용하여 묘사됩니다. 오른쪽에는 $mathcal{H}_4$ 내에서 가장 일관된("고전적") 기반 상태에 대한 Husimi 함수가 표시됩니다.

인기 요약

극한 상태(일관성 및 역간섭성)는 양자 계측에서 최적의 로토센서로 실용적으로 적용됩니다. 이 연구는 극한 스핀 일관성에 대한 Lüders 및 von Neumann의 최적 직교 측정을 제안하는 상태 검색에 관한 이전 연구의 자연스러운 확장을 제공합니다. $mathcal{B}_t$ 측정값을 $mathcal{H}_N$의 기준으로 제공되는 측정값의 양자성을 특성화하는 도구로 소개합니다. $N=3,4,5$ 및 $7$에 대해 가장 많은 양자 기반에 대한 검색이 수행됩니다. 수치 결과는 얻은 솔루션이 고유하다는 것을 시사합니다. 가장 스핀 일관성 있는 상태로 구성된 "고전적" 베이스에 대한 후보 세트는 $N=3,4,5,6$로 표시됩니다. 마조라나(Majorana)의 별 표현에서 분석된 대부분의 양자 기반 중 일부는 플라톤 입체의 대칭을 드러냅니다. 대부분의 고전적인 베이스는 대칭 구조도 표시합니다. 우리는 또한 주어진 기초를 형성하는 벡터의 양자성에 대한 다른 측정도 고려했습니다. $N$ 직교 벡터의 평균 Wehrl 엔트로피를 최적화하면 $N=6$에 대한 양자 기반을 제외하고 $mathcal{B}_t$ 수량의 극값으로 구별되는 동일한 베이스가 생성됩니다.

► BibTeX 데이터

► 참고 문헌

[1] T. Frankel, The Geometry of Physics: An Introduction, 3판, Cambridge University Press (2011).
https : / /doi.org/ 10.1017 / CBO9781139061377

[2] D. Chruściński 및 A. Jamiołkowski, 고전 및 양자역학의 기하학적 위상, Birkhäuser(2004).
https:/​/​doi.org/​10.1007/​978-0-8176-8176-0

[3] DA Lee, 기하 상대성 이론, 미국 수학회, 프로비던스(2021).
https : / /doi.org/ 10.1090 / gsm / 201

[4] I. Bengtsson 및 K. Życzkowski, 양자 상태 기하학: 양자 얽힘 소개, 2판, Cambridge University Press (2017).
https : / /doi.org/ 10.1017 / 9781139207010

[5] M. Lewin, 비선형 다체 양자 시스템의 기하학적 방법, J. Functional Analysis 260, 12, (2011).
https : / / doi.org/ 10.1016 / j.jfa.2010.11.017

[6] E. Cohen, H. Larocque, F. Bouchard 등, Aharonov-Bohm에서 Pancharatnam-Berry 및 그 이상까지의 기하학적 위상, Nat. 목사 물리. 1, 437–449(2019).
https:/​/​doi.org/​10.1038/​s42254-019-0071-1

[7] E. Campo 자기 변수의 Majorana Atomi orientati, Nuovo Cimento 9, 43-50 (1932).
https : / /doi.org/ 10.1007 / BF02960953

[8] R. Barnett, A. Turner 및 E. Demler, 스피너 원자의 새로운 단계 분류, Phys. Lett 목사. 97, 180412(2006).
https : / /doi.org/10.1103/ PhysRevLett.97.180412

[9] R. Barnett, A. Turner 및 E. Demler, $S=3$ Bose-Einstein 응축액의 소용돌이 분류, Phys. A 76, 013605(2007).
https : / /doi.org/10.1103/ PhysRevA.76.013605

[10] H. Mäkelä, K.-A. Suominen, 스핀 시스템의 불활성 상태, Phys. Lett 목사. 99, 190408(2007).
https : / /doi.org/10.1103/ PhysRevLett.99.190408

[11] E. Serrano-Ensástiga 및 F. Mireles, 스피너 Bose-Einstein 응축물의 위상 특성 분석: Majorana 항성 표현 접근법, Phys. 레트 사람. A 492, 129188(2023).
https : / /doi.org/ 10.1016 / j.physleta.2023.129188

[12] P. Mathonet 외, $N$-큐비트 대칭 상태의 얽힘 등가성, Phys. A 81, 052315(2010).
https : / /doi.org/10.1103/ PhysRevA.81.052315

[13] J. Martin, O. Giraud, PA Braun, D. Braun 및 T. Bastin, 높은 기하학적 얽힘을 갖는 다중큐비트 대칭 상태, Phys. A 81, 062347(2010).
https : / /doi.org/10.1103/ PhysRevA.81.062347

[14] M. Aulbach, DJH Markham 및 M. Murao, 기하학적 측정 측면에서 최대로 얽힌 대칭 상태, New J. Phys. 12, 073025(2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​7/​073025

[15] DJH Markham, 순열 대칭 상태의 얽힘 및 대칭, Phys. A 83, 042332(2011).
https : / /doi.org/10.1103/ PhysRevA.83.042332

[16] P. Ribeiro 및 R. Mosseri, $n$ 큐비트 대칭 섹터의 얽힘, Phys. Lett 목사. 106, 180502(2011).
https : / /doi.org/10.1103/ PhysRevLett.106.180502

[17] M.Aulbach, 대칭 상태의 얽힘 분류, Int. J. 양자 정보. 10, 1230004(2012).
https : / /doi.org/ 10.1142 / S0219749912300045

[18] W. Ganzzarek, M. Kuś 및 K. Życzkowski, 양자 얽힘의 무게 중심 측정, Phys. A 85, 032314(2012).
https : / /doi.org/10.1103/ PhysRevA.85.032314

[19] A. Mandilara, T. Coudreau, A. Keller 및 P. Milman, 스핀 일관성 상태를 통한 순수 대칭 상태의 얽힘 분류, Phys. A 90, 050302(R)(2014).
https : / /doi.org/10.1103/ PhysRevA.90.050302

[20] P. Hyllus, at al., Fisher 정보 및 다중 입자 얽힘, Phys. A 85, 022321(2012).
https : / /doi.org/10.1103/ PhysRevA.85.022321

[21] JH Hannay, 마조라나 표현의 스핀에 대한 베리 단계, J. Phys. 답: 수학. 31장, L53(1998).
https:/​/​doi.org/​10.1088/​0305-4470/​31/​2/​002

[22] P. Bruno, Majorana의 항성 표현의 양자 기하학적 위상: 다체 Aharonov-Bohm 위상에 매핑, Phys. Lett 목사. 108, 240402(2012).
https : / /doi.org/10.1103/ PhysRevLett.108.240402

[23] HD Liu, LB Fu, Majorana의 별 표현, Phys의 Berry 위상 및 양자 얽힘. A 94, 022123(2016).
https : / /doi.org/10.1103/ PhysRevA.94.022123

[24] P. Ribeiro, J. Vidal 및 R. Mosseri, Lipkin-Meshkov-Glick 모델의 열역학적 한계, Phys. Lett 목사. 99, 050402(2007).
https : / /doi.org/10.1103/ PhysRevLett.99.050402

[25] P. Ribeiro, J. Vidal 및 R. Mosseri, 열역학적 한계 및 유한 크기 보정에서 Lipkin-Meshkov-Glick 모델의 정확한 스펙트럼, Phys. E 78, 021106(2008).
https : / /doi.org/10.1103/ PhysRevE.78.021106

[26] J. Zimba, Majorana 표현을 통한 "반 응집성" 스핀 상태, Electron. J. 테오르. 물리. 3, 143(2006).
https:/ / api.semanticscholar.org/ CorpusID:13938120

[27] D. Baguette, T. Bastin 및 J. Martin, 최대 혼합 90 큐빗 감소를 갖는 멀티 큐빗 대칭 상태 Phys. 개정 A 032314, 2014 (XNUMX).
https : / /doi.org/10.1103/ PhysRevA.90.032314

[28] O. Giraud, D. Braun, D. Baguette, T. Bastin 및 J. Martin, 스핀 상태의 텐서 표현, Phys. Lett. 114, 080401 (2015).
https : / /doi.org/10.1103/ PhysRevLett.114.080401

[29] D. Baguette, F. Damanet, O. Giraud 및 J. Martin, 포인트 그룹 대칭을 갖는 스핀 상태의 반 일관성, Phys. 개정 A 92, 052333 (2015).
https : / /doi.org/10.1103/ PhysRevA.92.052333

[30] HD Liu, LB Fu, X. Wang, Majorana 표현을 위한 일관성 있는 상태 접근 방식, Commun. 이론. 물리. 67, 611(2017).
https:/​/​doi.org/​10.1088/​0253-6102/​67/​6/​611

[31] D. Baguette, J. Martin, 순수 스핀 상태에 대한 Anticoherence 측정, Phys. A 96, 032304(2017).
https : / /doi.org/10.1103/ PhysRevA.96.032304

[32] P. Kolenderski 및 R. Demkowicz-Dobrzański, 기준 좌표계 정렬 및 플라톤 입체를 유지하기 위한 최적 상태, Phys. A 78, 052333(2008).
https : / /doi.org/10.1103/ PhysRevA.78.052333

[33] C. Chryssomalakos 및 H. Hernández-Coronado, 최적의 양자 로토센서, Phys. A 95, 052125(2017).
https : / /doi.org/10.1103/ PhysRevA.95.052125

[34] AZ Goldberg 및 DFV James, 역간섭 상태를 사용한 양자 제한 오일러 각도 측정, Phys. A 98, 032113(2018).
https : / /doi.org/10.1103/ PhysRevA.98.032113

[35] J. Martin, S. Weigert 및 O. Giraud, 일관성 및 역간섭 상태에 의한 알 수 없는 축에 대한 회전의 최적 감지, Quantum 4, 285(2020).
https:/​/​doi.org/​10.22331/​q-2020-06-22-285

[36] J. Crann, DW Kribs 및 R. Pereira, 구형 디자인 및 반 응집성 스핀 상태, J. Phys. 답: 수학. 이론. 43, 255307(2010).
https:/​/​doi.org/​10.1088/​1751-8113/​43/​25/​255307

[37] E. Bannai 및 M. Tagami, 역 응집성 스핀 상태에 대한 참고 사항, J. Phys. 답: 수학. 이론. 44, 342002(2011).
https:/​/​doi.org/​10.1088/​1751-8113/​44/​34/​342002

[38] M. Wang, Y. Zhu, Anticoherent spin-2 상태 및 구형 디자인, J. Phys. 답: 수학. 이론. 55, 425304(2022).
https:/​/​doi.org/​10.1088/​1751-8121/​ac971d

[39] AZ Goldberg, AB Klimov, M.Grassl, G. Leuchs 및 LL Sánchez-Soto, 극한 양자 상태, AVS Quantum Sci. 2, 044701(2020).
https : / /doi.org/ 10.1116 / 5.0025819

[40] AZ Goldberg, M. Grassl, G. Leuchs 및 LL Sánchez-Soto, 얽힘을 넘어선 양자: 대칭 상태의 경우, Phys. A 105, 022433(2022).
https : / /doi.org/10.1103/ PhysRevA.105.022433

[41] O. Giraud, P. Braun 및 D. Braun, 양자성을 정량화하고 양자의 여왕에 대한 탐구, New J. Phys. 12, 063005(2010).
https:/​/​doi.org/​10.1088/​1367-2630/​12/​6/​063005

[42] R. Delbourgo, 회전 그룹 및 연합 그룹에 대한 최소 불확실성 상태, J. Phys. A 10, L233(1977).
https:/​/​doi.org/​10.1088/​0305-4470/​10/​11/​012

[43] A. Wehrl, 고전적 엔트로피와 양자역학적 엔트로피 사이의 관계에 대해, Rep. Math. 물리. 16, 353(1979).
https:/​/​doi.org/​10.1016/​0034-4877(79)90070-3

[44] EH Lieb, Wehrl의 엔트로피 추측 증명, Commun. 수학. 물리. 62, 35(1978).
https : / /doi.org/ 10.1007 / BF01940328

[45] CT Lee, Wehrl의 스핀 상태 엔트로피 및 Lieb의 추측, J. Phys. A 21, 3749(1988).
https:/​/​doi.org/​10.1088/​0305-4470/​21/​19/​013

[46] EH Lieb 및 JP Solovej, Bloch 응집성 스핀 상태 및 일반화에 대한 엔트로피 추측 증명, Acta Math. 212, 379(2014).
https:/​/​doi.org/​10.1007/​s11511-014-0113-6

[47] F. Bouchard, 외., 극단 마요라나 별자리의 한계에 있는 양자 계측학, Optica 4, 1429-1432 (2017).
https : / /doi.org/ 10.1364 / OPTICA.4.001429

[48] A. Wehrl, 엔트로피의 일반 특성, Rev. Mod. 물리. 50, 221(1978).
https : / /doi.org/10.1103/ RevModPhys.50.221

[49] A. Wehrl, 엔트로피의 다양한 측면, 수학 대표. 물리. 30, 119(1991).
https:/​/​doi.org/​10.1016/​0034-4877(91)90045-O

[50] S. Gnutzmann 및 K. Życzkowski, 위상 공간의 국소화 측정으로서 Renyi-Wehrl 엔트로피, J. Phys. A 34, 10123(2001).
https:/​/​doi.org/​10.1088/​0305-4470/​34/​47/​317

[51] K. Życzkowski, 고유 상태의 국소화 및 평균 Wehrl 엔트로피, Physica E 9, 583 (2001).
https:/​/​doi.org/​10.1016/​S1386-9477(00)00266-6

[52] LL Sánchez-Soto, AB Klimov, P. de la Hoz 및 G. Leuchs, 양자 대 고전적 편광 상태: 다중극이 계산될 때, J. Phys. B 46 104011(2013).
https:/​/​doi.org/​10.1088/​0953-4075/​46/​10/​104011

[53] A. Tavakoli 및 N. Gisin, 플라톤 입체 및 양자 역학의 기본 테스트, Quantum 4, 293 (2020).
https:/​/​doi.org/​10.22331/​q-2020-07-09-293

[54] H.Ch. Nguyen, S. Designolle, M. Barakat 및 O. Gühne, 양자 역학 측정 간 대칭, 사전 인쇄 arXiv:2003.12553(2022).
https://​/​doi.org/​10.48550/​arXiv.2003.12553
arXiv : 2003.12553

[55] JI Latorre, G. Sierra, 플라톤 얽힘, Quantum Inf. 계산. 21, 1081(2021).
https : / / doi.org/ 10.26421 / QIC21.13-14-1

[56] K. Bolonek-Lasoń 및 P. Kosiński, 그룹, 플라톤 다면체 및 벨 부등식, Quantum 5, 593 (2021).
https:/​/​doi.org/​10.22331/​q-2021-11-29-593

[57] KF Pál 및 T. Vértesi, 그룹, 모든 차원에 대한 플라톤 벨 불평등, Quantum 6, 756(2022).
https:/​/​doi.org/​10.22331/​q-2022-07-07-756

[58] RH Dicke, 자발 방사선 과정의 일관성, Phys. 개정 93, 99(1954).
https : / /doi.org/10.1103/ PhysRev.93.99

[59] V. Karimipour 및 L. Memarzadeh, 임의 차원의 등위 얽힌 베이스 Phys. A 73, 012329(2006).
https : / /doi.org/10.1103/ PhysRevA.73.012329

[60] G. Rajchel, A. Gąsiorowski 및 K. Życzkowski, Robust Hadamard 행렬, Birkhoff 폴리토프의 비비속적 광선 및 복합 공간의 등얽힌 베이스 수학. 비교. 과학. 12, 473(2018).
https : / /doi.org/ 10.1007 / s11786-018-0384-y

[61] J. Czartowski, D. Goyeneche, M. Grassl 및 K. Życzkowski, 등얽힌 상호 편향 베이스, 대칭 양자 측정 및 혼합 상태 설계, Phys. Lett 목사. 124, 090503(2020).
https : / /doi.org/10.1103/ PhysRevLett.124.090503

[62] F. Del Santo, J. Czartowski, K. Życzkowski 및 N. Gisin, Iso 얽힌 베이스 및 관절 측정, 사전 인쇄 arXiv:2307.06998(2023).
https://​/​doi.org/​10.48550/​arXiv.2307.06998
arXiv : 2307.06998

[63] R. Penrose, On Bell 비국소성(확률 없음: 일부 흥미로운 기하학), Quantum Reflections(2000).

[64] J. Zimba 및 R. Penrose, 확률 없는 벨 비국소성: 더 흥미로운 기하학, Stud. 역사. 필. 과학. 24, 697(1993).
https:/​/​doi.org/​10.1016/​0039-3681(93)90061-N

[65] JE Massad, 및 PK Aravind, The Penrose 정십이면체 재검토, Am. J. 물리학 67, 631(1999).
https : / /doi.org/ 10.1119 / 1.19336

[66] K. Husimi, 밀도 매트릭스의 일부 형식적 속성, Proc. 물리. 수학. Soc. 22, 264(1940).
https : / / doi.org/ 10.11429 / ppmsj1919.22.4_264

[67] W. Słomczyński 및 K. Życzkowski, 구에서 양자 지도의 평균 동적 엔트로피는 준고전적 한계인 Phys에서 발산됩니다. Lett 목사. 80, 1880(1998).
https : / /doi.org/10.1103/ PhysRevLett.80.1880

[68] M. Piotrak, M. Kopciuch, AD Fard, M. Smolis, S. Pustelny, K. Korzekwa, 완벽한 양자 각도기, 사전 인쇄 arXiv:2310.13045(2023).
https://​/​doi.org/​10.48550/​arXiv.2310.13045
arXiv : 2310.13045

[69] NCN Maestro 7 2015/​18/​A/​ST2/​00274 웹사이트 https:/​/​chaos.if.uj.edu.pl/​ karol/​Maestro7/​files/​data3/​Numerical_Results.dat.
https:/​/​chaos.if.uj.edu.pl/​~karol/​Maestro7/​files/​data3/​Numerical_Results.dat

[70] D. Weingarten, 무한 순위의 한계에서 그룹 적분의 점근적 동작, J. Math. 물리. 19, 999(1978).
https : / /doi.org/ 10.1063 / 1.523807

[71] B. Collins 및 P. Śniady, 단일, 직교 및 대칭 그룹에 대한 Haar 측정과 관련된 통합, Commun. 수학. 물리. 264, 773(2006).
https:/​/​doi.org/​10.1007/​s00220-006-1554-3

[72] G. Rajchel, 양자 매핑 및 설계, 박사 학위 논문, 사전 인쇄 arXiv:2204.13008(2022).
https://​/​doi.org/​10.48550/​arXiv.2204.13008
arXiv : 2204.13008

[73] D. Martin, EP Wigner, 그룹 이론 및 원자 스펙트럼의 양자 역학에 대한 적용, Academic Press Inc. NY (1959).
https:/​/​doi.org/​10.1016/​b978-0-12-750550-3.x5001-0

인용

[1] Michał Piotrak, Marek Kopciuch, Arash Dezhang Fard, Magdalena Smolis, Szymon Pustelny 및 Kamil Korzekwa, "완벽한 양자 각도기", arXiv : 2310.13045, (2023).

[2] Aaron Z. Goldberg, "대칭 상태의 입자 하위 집합에 대한 상관 관계: 나머지가 무시될 때 광자가 광선 내에서 수행하는 작업", arXiv : 2401.05484, (2024).

위의 인용은 SAO / NASA ADS (마지막으로 성공적으로 업데이트 됨 2024-01-25 23:58:21). 모든 출판사가 적절하고 완전한 인용 데이터를 제공하지는 않기 때문에 목록이 불완전 할 수 있습니다.

On Crossref의 인용 서비스 인용 작품에 대한 데이터가 없습니다 (최종 시도 2024-01-25 23:58:19).

이 백서는 Quantum에서 Creative Commons Attribution 4.0 International(CC BY 4.0) 특허. 저작권은 저자 또는 기관과 같은 원래 저작권 보유자에게 있습니다.

타임 스탬프 :

더보기 양자 저널