1ICFO-Institut de Ciencies Fotoniques, 바르셀로나 과학 기술 연구소, 08860 Castelldefels, 스페인
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 바르셀로나, 스페인
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 그르노블, 프랑스
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spain
이 논문이 흥미 롭거나 토론하고 싶습니까? SciRate에 댓글을 달거나 댓글 남기기.
추상
상호 편향되지 않은 염기는 양자 정보 이론에서 매우 유용한 측정 쌍에 해당합니다. 가장 작은 합성 차원인 2에서 83개에서 062303개 사이의 상호 편향되지 않은 염기가 존재하는 것으로 알려져 있으며, Zauner의 추측으로 알려진 수십 년 된 추측에 따르면 기껏해야 2011개가 존재한다고 합니다. 여기서 우리는 $n$ MUB가 해당 차원에 존재하는 경우에만 $d$ 차원에서 최대로 위반될 수 있는 모든 정수 쌍 $n,d ge XNUMX$에 대한 Bell 부등식의 구성을 통해 Zauner의 추측을 수치적으로 처리합니다. 따라서 우리는 Zauner의 추측을 최적화 문제로 전환하고 세 가지 수치적 방법인 시소 최적화, 비선형 준정확 프로그래밍 및 몬테카를로 기법을 통해 해결합니다. 세 가지 방법 모두 낮은 차원에서 알려진 사례를 정확하게 식별하고 모두 XNUMX차원에서 XNUMX개의 상호 편향되지 않은 기준이 존재하지 않음을 제안하며, 모두 해당 Bell 부등식을 수치적으로 최적화하는 동일한 기준을 찾습니다. 더욱이, 이러한 수치적 옵티마이저는 [P. Raynal, X.Lü, B.-G. Englert, {Phys. A}, {XNUMX} XNUMX(XNUMX)]. 마지막으로 Monte Carlo 결과는 최대 XNUMX개의 MUB가 차원 XNUMX에 존재함을 시사합니다.
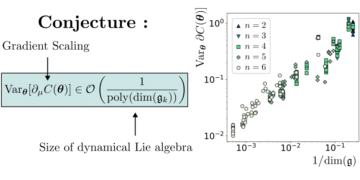
주요 이미지: n MUB가 차원 d에 존재한다고 가정하는 Bell 부등식의 값과 수치적 방법으로 찾은 값 사이의 상대적인 차이입니다. XNUMX 값은 메서드가 차원 d에서 n MUB를 찾았음을 의미하고, XNUMX이 아닌 값은 메서드가 차원 d에서 n MUB를 찾지 못했음을 의미합니다. 모든 알려진 사례(차원 XNUMX~XNUMX, 차원 XNUMX과 XNUMX~XNUMX개의 MUB)는 숫자로 정확하게 식별됩니다. XNUMX차원에서 어떤 방법도 XNUMX개의 MUB를 찾지 못하고 모든 방법이 동일한 XNUMX개의 기본 세트로 수렴됩니다.
인기 요약
MUB의 광범위한 사용에도 불구하고 MUB의 구조에 관한 미해결 질문이 여전히 남아 있습니다. 가장 눈에 띄는 점은 양자 시스템의 차원이 복합 숫자인 경우 쌍으로 편향되지 않은 최대 측정 수("MUB 수")를 알 수 없다는 것입니다. 특히 XNUMX차원에서는 MUB의 수가 XNUMX에서 XNUMX 사이라는 것만 알 수 있습니다. 오래 지속된 열린 추측은 Zauner의 추측으로, XNUMX차원에는 XNUMX개 이상의 MUB가 존재하지 않는다는 것입니다. 수십 년에 걸친 이 추측은 몇 가지 수치적 증거로 뒷받침되지만 오늘날까지 증거는 없습니다.
이 작업에서 우리는 Bell 비국소성을 통해 Zauner의 추측을 다룹니다. Bell 비국소성은 통신이 허용되지 않지만 고전적인 임의성 또는 공유 양자 상태의 형태로 일부 상관 관계를 공유할 수 있는 두 명의 실험자와 관련됩니다. 양자 자원을 공유하면 고전 물리학(보다 정확하게는 소위 숨겨진 로컬 변수 모델)으로 설명할 수 없는 실험 데이터가 생성될 수 있음이 밝혀졌습니다. 이것은 벨의 정리(Bell's theorem)로 알려져 있으며 지난 XNUMX년 동안 실험적으로 검증되었습니다. 실험 데이터의 비고전성을 목격하는 것은 실험에서 발생하는 측정 결과 확률의 함수인 소위 벨 부등식을 통해 가장 일반적으로 수행됩니다. 고전 데이터는 Bell 부등식을 충족해야 하지만 양자 데이터는 이를 위반할 수 있습니다.
최근에 당사자 중 하나가 주어진 차원의 한 쌍의 MUB 측정을 사용하는 경우 최대로 위반되는 Bell 부등식이 발견되었습니다. 이 작업에서는 이러한 불평등을 주어진 차원에서 선택한 MUB 측정 수에 의해 최대로 위반되는 새로운 불평등으로 확장합니다. 또한 실험의 차원이 고정된 경우 사용된 측정값이 주어진 차원에서 선택한 MUB 수에 해당하는 경우에만 최대 위반이 얻어집니다. 따라서 주어진 차원에 선택된 수의 MUB가 존재하는지 여부를 결정하는 것은 이 고정 차원에서 해당 벨 부등식의 최대 위반을 찾는 것과 같습니다.
이 최대 위반을 찾는 것은 일반적으로 어려운 문제이지만 고정 차원에서 Bell 부등식의 최대 위반을 찾으려는 시도로 세 가지 수치 방법을 사용합니다. 이러한 방법 중 두 가지는 준정확 프로그래밍 기술의 변형이며, 세 번째 방법은 통계 물리학에서 영감을 받아 시뮬레이션 어닐링이라고 합니다. 이러한 모든 방법은 휴리스틱(즉, 문제의 진정한 최적을 찾을 것이라는 보장이 없음)하지만 최적이 알려진 최적화 문제에 적용하여 성능을 측정할 수 있습니다. 특히, 세 가지 방법 모두 존재하는 것으로 알려진 경우 MUB 측정을 올바르게 식별할 수 있음을 발견했습니다. 또한 존재하지 않는 것으로 알려진 경우 세 가지 방법 모두 수치 정밀도까지 동일한 측정 세트로 수렴됩니다. 그런 다음 방법을 첫 번째 알려지지 않은 사례, 즉 XNUMX차원에 있는 XNUMX개의 MUB에 적용합니다. 어떤 방법도 XNUMX차원에서 XNUMX개의 MUB를 식별할 수 없지만 다시 수치 정밀도까지 모두 동일한 XNUMX개의 측정 세트로 수렴됩니다. 더욱이, 모의 어닐링 기술은 다음 복합 차원인 차원 XNUMX에서 XNUMX개의 MUB를 찾지 않습니다. 따라서 우리 기술의 휴리스틱 특성으로 인해 엄격한 주장을 할 수는 없지만 우리의 결과는 Bell 비국소성의 새로운 관점에서 Zauner의 추측을 뒷받침합니다.
► BibTeX 데이터
► 참고 문헌
[1] ID 이바노비치. 양자 상태 결정의 기하학적 설명. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. 브라사드 CH 베넷. 양자 암호화: 공개 키 배포 및 동전 던지기. 컴퓨터, 시스템 및 신호 처리에 관한 IEEE 국제 회의(IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https : / /doi.org/ 10.1016 / j.tcs.2011.08.039
[3] 아서 K. 에커트. Bell의 정리에 기반한 양자 암호. 물리학 Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https : / /doi.org/10.1103/ PhysRevLett.67.661
[4] 다그마르 브루스. 81가지 상태의 양자 암호학에서 최적의 도청. 물리학 Lett., 3018:3021–1998, 10.1103. doi:81.3018/PhysRevLett.XNUMX.
https : / /doi.org/10.1103/ PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques, Mohamed Bourennane. 단일 $d$ 수준 시스템을 사용하는 양자 임의 액세스 코드. 물리학 Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https : / /doi.org/10.1103/ PhysRevLett.114.170502
[6] Máté Farkas와 Jędrzej Kaniewski. 준비 및 측정 시나리오에서 상호 편향되지 않은 기반을 자체 테스트합니다. 물리학 A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https : / /doi.org/10.1103/ PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci 및 N. Gisin. 이진 측정을 사용하는 qunits에 대한 벨 부등식. 양자정보 Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https : / /doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos 및 Remigiusz Augusiak. 최대 얽힘 및 상호 편향되지 않은 기반 및 3쿼트 양자 시스템의 자체 테스트로 인한 최대 비국소성. Quantum, 198:2019, 10.22331. doi:2019/q-10-24-198-XNUMX.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal, Jędrzej Kaniewski. Bell 실험에서 상호 편향되지 않은 염기 및 대칭 정보로 완전한 측정. 사이언스 어드밴스, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson, Karol Życzkowski. 상호 공평한 기반에서. 국제 양자 정보 저널, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https : / /doi.org/ 10.1142 / S0219749910006502
[11] 윌리엄 K 우터스와 브라이언 D 필즈. 상호 편향되지 않은 측정에 의한 최적의 상태 결정. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan과 Thomas Beth. 정사각형 차원에서 상호 편향되지 않은 베이스의 새로운 구조. 양자정보 Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https : / /doi.org/ 10.26421 / QIC5.2-1
[13] 미하이 와이너. 상호 편향되지 않은 염기의 최대 수에 대한 간격입니다. 절차 아메르. 수학. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] 게르하르트 자우너. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. 박사 논문, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep, Pawel Wocjan. 거짓말 대수학의 상호 편향되지 않은 염기 및 직교 분해. 양자정보 Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https : / /doi.org/ 10.26421 / QIC7.4-6
[16] 스티븐 브리얼리와 스테판 바이거트. 79차원에서 상호 공평한 기반을 구축합니다. 물리학 A, 052316:2009, 10.1103. doi:79.052316/PhysRevA.XNUMX.
https : / /doi.org/10.1103/ PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi, Mihály Weiner. 일반화된 Pauli 문제 및 차원 6의 MUB-삼중항 무한 패밀리. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, 2009년 10.1088월. doi:1751/ 8113-42/ 24/ 245305/ XNUMX.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] 게리 맥코넬, 해리 스펜서, 아파크 타히르. $mathbb{C}^6$에서 Zauner의 MUB 추측에 대한 증거. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] 샌더 그리블링과 스벤 폴락. 상호 편향되지 않은 염기: 다항식 최적화 및 대칭. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej, Karol Życzkowski. 상호 편향되지 않은 염기와 48차 Hadamard 행렬. 수리 물리학 저널, 5(052106):2007, 10.1063. doi:1.2716990/XNUMX.
https : / /doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü, Berthold-Georg Englert. 83차원에서 상호 편견 없는 기지: 가장 먼 기지 062303개. 물리학 A, 2011:10.1103, 83.062303. doi:XNUMX/PhysRevA.XNUMX.
https : / /doi.org/10.1103/ PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz, Marcin Pawłowski. 상호 편향되지 않은 기반과 양자 임의 액세스 코드 간의 연결. 물리학 Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https : / /doi.org/10.1103/ PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani 및 Stephanie Wehner. 벨 비 지역성. Rev. Mod. Phys., 86 : 419–478, 2014. doi : 10.1103 / RevModPhys.86.419.
https : / /doi.org/10.1103/ RevModPhys.86.419
[24] 모세크 ApS. C++용 MOSEK 퓨전 API 9.2.49, 2021. URL: https:/ / docs.mosek.com/ 9.2/ cxxfusion/ index.html.
https:/ / docs.mosek.com/ 9.2/ cxxfusion/ index.html
[25] 야마시타 히로시, 야베 히로시, 하라다 코우헤이. 비선형 반정부 계획법을 위한 원시-이중 내부 점 방법입니다. 수학 프로그래밍, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https : / /doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd와 Lieven Vandenberghe. 볼록 최적화. Cambridge University Press, 2004. doi : 10.1017 / CBO9780511804441.
https : / /doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt 및 MP Vecchi. 모의 어닐링에 의한 최적화. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https : / /doi.org/10.1126/ science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller 및 Edward Teller. 빠른 컴퓨팅 기계에 의한 상태 계산 방정식. 화학 물리학 저널, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https : / /doi.org/ 10.1063 / 1.1699114
[29] 미구엘 나바스쿠에스, 스테파노 피로니오, 안토니오 아신. 양자 상관 세트의 경계. 물리학 Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https : / /doi.org/10.1103/ PhysRevLett.98.010401
인용
이 백서는 Quantum에서 Creative Commons Attribution 4.0 International(CC BY 4.0) 특허. 저작권은 저자 또는 기관과 같은 원래 저작권 보유자에게 있습니다.