In 1850, Thomas Penyngton Kirkman, een wiskundige toen hij zijn hoofdverantwoordelijkheid als predikant in de Church of England niet vervulde, beschreef zijn "schoolmeisjesprobleem": ze dagelijks, zodat geen twee twee keer naast elkaar lopen.”
Voor een moderne wiskundige kan dit soort probleem het beste worden voorgesteld als een hypergraaf - een reeks knooppunten verzameld in groepen van drie of meer. De 15 schoolmeisjes zijn knooppunten en elke groep van "drie op de hoogte" kan worden gezien als een driehoek, met drie lijnen of randen, die drie knooppunten verbinden.
Het probleem van Kirkman vraagt in wezen of er een rangschikking van deze driehoeken is die alle schoolmeisjes met elkaar verbindt, maar met de extra beperking dat geen twee driehoeken een rand delen. Edge-sharing zou betekenen dat twee schoolmeisjes meer dan eens samen moeten lopen. Deze beperking houdt in dat elk meisje een week lang elke dag met twee nieuwe vrienden wandelt, zodat elk mogelijk paar precies één keer samenkomt.
Dit probleem en soortgelijke problemen hebben wiskundigen al bijna twee eeuwen verleid sinds Kirkman zijn vraag stelde. In 1973 poseerde de legendarische wiskundige Paul Erdős voor een soortgelijke. Hij vroeg of het mogelijk is om een hypergraaf te bouwen met twee schijnbaar onverenigbare eigenschappen. Ten eerste moet elk paar knopen worden verbonden door precies één driehoek, zoals bij de schoolmeisjes. Deze eigenschap maakt de grafiek dicht met driehoeken. De tweede vereiste dwingt de driehoeken om op een zeer nauwkeurige manier uit te spreiden. (Het vereist met name dat er voor elke kleine groep driehoeken minstens drie knopen meer zijn dan er driehoeken zijn.) "Je hebt dit enigszins tegenstrijdige gedrag waarbij je een dicht algemeen object hebt dat geen dichte delen heeft," zei David Conlon, een wiskundige aan het California Institute of Technology.
Deze januari, in een ingewikkeld bewijs van 50 pagina's, bewezen vier wiskundigen dat het altijd mogelijk is om zo'n hypergraaf te bouwen zolang je maar genoeg knooppunten hebt. "De hoeveelheid technische details die [ze] hebben doorgemaakt, gewoon om dit te krijgen, het was geweldig", zei Allan Lo, een wiskundige aan de Universiteit van Birmingham. Conlon was het daarmee eens: "Het is echt een indrukwekkend stuk werk."
Het onderzoeksteam bouwde een systeem dat aan de duivelse eisen van Erdős voldeed door te beginnen met een willekeurig proces om driehoeken te kiezen en dit met uiterste zorg te ontwerpen om aan hun behoeften te voldoen. "Het aantal moeilijke wijzigingen dat in het bewijs wordt gebruikt, is eigenlijk onthutsend", zei Conlon.
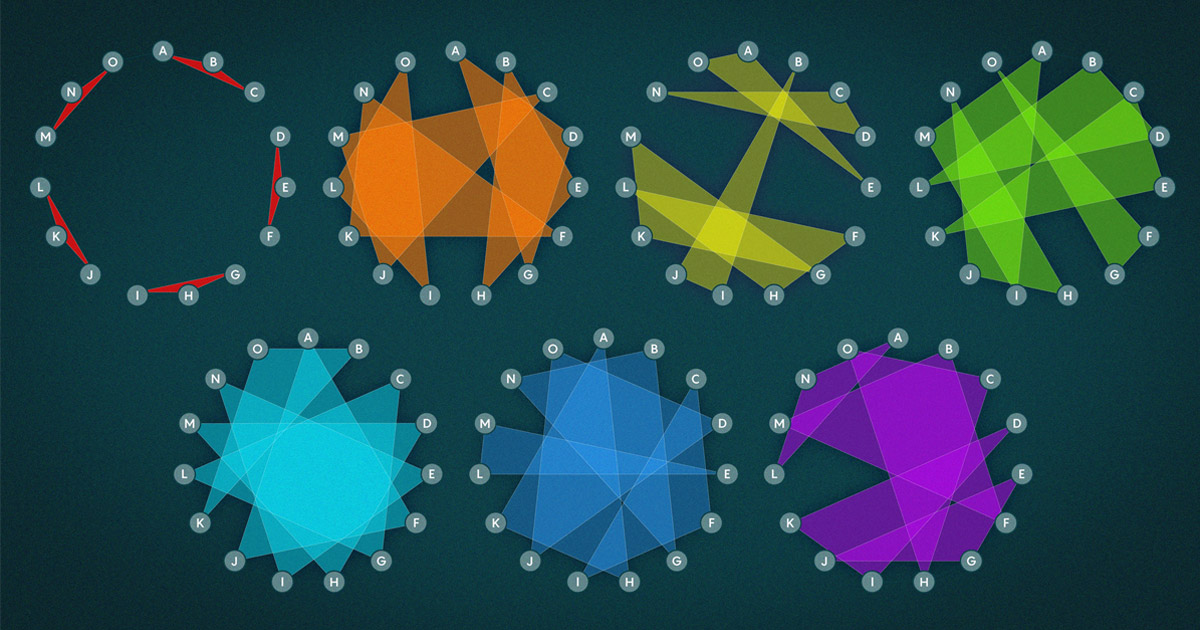
Hun strategie was om de hypergraaf zorgvuldig uit afzonderlijke driehoeken te bouwen. Stel je bijvoorbeeld onze 15 schoolmeisjes voor. Trek een lijn tussen elk paar.
Het doel hier is om driehoeken op deze lijnen te tekenen, zodat de driehoeken aan twee vereisten voldoen: Ten eerste delen geen twee driehoeken een rand. (Systemen die aan deze vereiste voldoen, worden drievoudige Steiner-systemen genoemd.) En ten tweede, zorg ervoor dat elke kleine subset van driehoeken een voldoende groot aantal knooppunten gebruikt.
De manier waarop de onderzoekers dit deden, is misschien het best te begrijpen met een analogie.
Stel dat je in plaats van driehoeken van randen te maken, huizen bouwt van Legoblokjes. De eerste paar gebouwen die je maakt zijn extravagant, met structurele versterkingen en uitgebreide versieringen. Als je hiermee klaar bent, leg je ze opzij. Ze zullen dienen als een "absorbeerder" - een soort gestructureerde voorraad.
Begin nu met het maken van gebouwen van je overgebleven stenen, zonder veel planning. Wanneer je aanbod van Lego afneemt, kun je merken dat je wat verdwaalde stenen hebt of huizen die structureel ondeugdelijk zijn. Maar omdat de absorberende gebouwen zo overdreven en versterkt zijn, kun je hier en daar wat stenen plukken en ze gebruiken zonder catastrofes te veroorzaken.
In het geval van het Steiner triple systeem probeer je driehoeken te maken. Uw absorber is in dit geval een zorgvuldig gekozen verzameling randen. Als u merkt dat u de rest van het systeem niet in driehoeken kunt sorteren, kunt u enkele randen gebruiken die naar de absorber leiden. Als je daarmee klaar bent, deel je de absorber zelf op in driehoeken.
Absorptie werkt niet altijd. Maar wiskundigen hebben aan het proces gesleuteld en nieuwe manieren gevonden om obstakels te omzeilen. Een krachtige variant genaamd iteratieve absorptie verdeelt bijvoorbeeld de randen in een geneste reeks sets, zodat elk als een absorptiemiddel voor de volgende grootste fungeert.
"In de afgelopen tien jaar zijn er enorme verbeteringen geweest", zegt Conlon. "Het is een soort kunstvorm, maar ze hebben het op dit moment echt naar het niveau van hoge kunst gebracht."
Erdős' probleem was lastig, zelfs met iteratieve absorptie. "Het werd vrij snel duidelijk waarom dit probleem niet was opgelost," zei Mehtaab Sawhney, een van de vier onderzoekers die het hebben opgelost, samen met Ashwin Saho, die samen met Sawhney een afgestudeerde student is aan het Massachusetts Institute of Technology; Michaël Simkin, een postdoctoraal fellow bij het Center of Mathematical Sciences and Applications aan de Harvard University; en Matthew Kwan, een wiskundige aan het Instituut voor Wetenschap en Technologie Oostenrijk. "Er waren behoorlijk interessante, behoorlijk moeilijke technische taken."
Bijvoorbeeld, in andere toepassingen van iteratieve absorptie, als je eenmaal klaar bent met het afdekken van een set - ofwel met driehoeken, voor Steiner drievoudige systemen, of met andere structuren voor andere problemen - kun je het als afgehandeld beschouwen en het vergeten. De omstandigheden van Erdős verhinderden echter dat de vier wiskundigen dat deden. Een problematisch cluster van driehoeken kan gemakkelijk knooppunten van meerdere absorptiesets omvatten.
"Een driehoek die je 500 stappen geleden hebt gekozen, je moet op de een of andere manier onthouden hoe je daarover moet denken", zei Sawhney.
Wat de vier uiteindelijk ontdekten, was dat als ze hun driehoeken zorgvuldig kozen, ze de noodzaak konden omzeilen om elk klein ding bij te houden. "Het is beter om na te denken over een kleine reeks van 100 driehoeken en te garanderen dat de reeks driehoeken met de juiste waarschijnlijkheid wordt gekozen", zei Sawhney.
De auteurs van het nieuwe artikel zijn optimistisch dat hun techniek verder kan worden uitgebreid dan dit ene probleem. Zij hebben hebben hun strategie al toegepast tot een probleem over Latijnse vierkanten, die lijken op een vereenvoudiging van een sudoku-puzzel.
Verder zijn er verschillende vragen die uiteindelijk kunnen leiden tot absorptiemethoden, zei Kwan. "Er zijn zoveel problemen in combinatoriek, vooral in ontwerptheorie, waar willekeurige processen een echt krachtig hulpmiddel zijn." Een zo'n probleem, het vermoeden van Ryser-Brualdi-Stein, gaat ook over Latijnse vierkanten en wacht al sinds de jaren zestig op een oplossing.
Hoewel absorptie mogelijk verdere ontwikkeling nodig heeft voordat het dat probleem kan oplossen, heeft het een lange weg afgelegd sinds het begin 30 geleden, zei: Maya Stein, de adjunct-directeur van het Centrum voor Wiskundige Modellering aan de Universiteit van Chili. "Dat is echt geweldig om te zien, hoe deze methoden evolueren."