1ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Castelldefels, Spanje
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spanje
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Frankrijk
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spanje
Vind je dit artikel interessant of wil je het bespreken? Scite of laat een reactie achter op SciRate.
Abstract
Wederzijds onbevooroordeelde basen komen overeen met zeer bruikbare meetparen in de kwantuminformatietheorie. In de kleinste samengestelde dimensie, zes, is bekend dat er tussen de drie en zeven onderling onbevooroordeelde bases bestaan, met een decennia oud vermoeden, bekend als het vermoeden van Zauner, dat stelt dat er maximaal drie bestaan. Hier pakken we het vermoeden van Zauner numeriek aan door Bell-ongelijkheden te construeren voor elk paar gehele getallen $n,d ge 2$ dat maximaal geschonden kan worden in dimensie $d$ als en slechts als $n$ MUB's bestaan in die dimensie. Vandaar dat we het vermoeden van Zauner omzetten in een optimalisatieprobleem, dat we aanpakken door middel van drie numerieke methodes: wip-optimalisatie, niet-lineair semidefiniet programmeren en Monte Carlo-technieken. Alle drie de methoden identificeren de bekende gevallen in lage dimensies correct en ze suggereren allemaal dat er geen vier onderling onbevooroordeelde bases in dimensie zes bestaan, waarbij ze allemaal dezelfde bases vinden die de overeenkomstige Bell-ongelijkheid numeriek optimaliseren. Bovendien lijken deze numerieke optimalisaties samen te vallen met de "vier meest afgelegen bases" in dimensie zes, gevonden door numerieke optimalisatie van een afstandsmaat in [P. Raynal, X. Lü, B.-G. Engelert, {Phys. Rev. A}, {83} 062303 (2011)]. Ten slotte suggereren de Monte Carlo-resultaten dat er maximaal drie MUB's bestaan in dimensie tien.
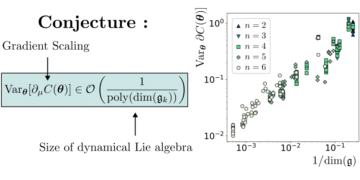
Uitgelichte afbeelding: het relatieve verschil tussen de waarde van onze Bell-ongelijkheden, ervan uitgaande dat n MUB's bestaan in dimensie d en de waarde gevonden door onze numerieke methoden. Nulwaarden betekenen dat de methoden n MUB's hebben gevonden in dimensie d, terwijl niet-nulwaarden betekenen dat de methoden geen n MUB's hebben gevonden in dimensie d. Alle bekende gevallen (dimensies twee tot vijf en dimensie zes met twee en drie MUB's) worden correct geïdentificeerd door de cijfers. In dimensie zes vindt geen van de methoden vier MUB's, en alle methoden convergeren naar dezelfde set van vier bases.
Populaire samenvatting
Ondanks hun brede gebruik blijven er nog open vragen over de structuur van MUB's. Het meest opvallende is dat het maximale aantal metingen dat paarsgewijze onbevooroordeeld is ("het aantal MUB's") onbekend is als de dimensie van het kwantumsysteem een samengesteld getal is. Met name in dimensie zes weten we alleen dat het aantal MUB's tussen drie en zeven ligt. Een al lang bestaand open vermoeden is dat van Zauner, die stelt dat er niet meer dan drie MUB's bestaan in dimensie zes. Dit decennialange vermoeden wordt ondersteund door enig numeriek bewijs, maar tot op de dag van vandaag bestaat er geen bewijs.
In dit werk pakken we het vermoeden van Zauner aan via Bell-non-lokaliteit. Bell non-lokaliteit betreft twee onderzoekers die niet mogen communiceren, maar wel enkele correlaties kunnen delen in de vorm van klassieke willekeur of een gedeelde kwantumtoestand. Het is aangetoond dat het delen van kwantumbronnen kan leiden tot experimentele gegevens die niet kunnen worden verklaard door de klassieke fysica (meer precies, door zogenaamde lokale modellen met verborgen variabelen). Dit staat bekend als de stelling van Bell en is de afgelopen tien jaar experimenteel geverifieerd. Getuige zijn van de niet-classiciteit van experimentele gegevens wordt meestal gedaan via zogenaamde Bell-ongelijkheden, die functies zijn van de meetuitkomstkansen die in het experiment voorkomen. Klassieke gegevens moeten voldoen aan Bell-ongelijkheden, terwijl kwantumgegevens deze kunnen schenden.
Onlangs zijn Bell-ongelijkheden gevonden die maximaal worden geschonden als een van de partijen een paar MUB-metingen van een bepaalde dimensie gebruikt. In dit werk breiden we deze ongelijkheden uit naar nieuwe, maximaal geschonden door een geselecteerd aantal MUB-metingen in een bepaalde dimensie. Bovendien, als de dimensie in het experiment vaststaat, wordt de maximale overtreding verkregen als en alleen als de gebruikte metingen overeenkomen met het geselecteerde aantal MUB's in de gegeven dimensie. Daarom is het beslissen of een geselecteerd aantal MUB's in een bepaalde dimensie bestaat, gelijk aan het vinden van de maximale schending van de overeenkomstige Bell-ongelijkheid in deze vaste dimensie.
Hoewel het vinden van deze maximale schending over het algemeen een moeilijk probleem is, gebruiken we drie verschillende numerieke methoden om de maximale schending van onze Bell-ongelijkheden in een vaste dimensie te vinden. Twee van deze methoden zijn varianten van semi-definitieve programmeertechnieken, terwijl de derde is geïnspireerd door statistische fysica en gesimuleerde annealing wordt genoemd. Hoewel al deze methoden heuristisch zijn - dat wil zeggen, er is geen garantie dat ze het echte optimum van het probleem zullen vinden - kan men hun prestaties meten door ze toe te passen op optimalisatieproblemen waarvan het optimum bekend is. In het bijzonder vinden we dat alle drie de methoden correct in staat zijn om MUB-metingen te identificeren in de gevallen waarvan bekend is dat ze bestaan. Bovendien, in de gevallen waarvan bekend is dat ze niet bestaan, convergeren alle drie de methoden naar dezelfde reeks metingen tot numerieke precisie. Vervolgens passen we onze methoden toe op het eerste onbekende geval, dat wil zeggen vier MUB's in dimensie zes. Geen van de methoden is in staat om vier MUB's in dimensie zes te identificeren, maar nogmaals, ze convergeren allemaal naar dezelfde set van vier metingen tot op numerieke precisie. Bovendien vindt de gesimuleerde uitgloeitechniek geen vier MUB's in de volgende samengestelde dimensie, dimensie tien. Daarom, hoewel rigoureuze claims niet kunnen worden gemaakt vanwege de heuristische aard van onze technieken, ondersteunen onze resultaten het vermoeden van Zauner vanuit het nieuwe perspectief van Bell-non-lokaliteit.
► BibTeX-gegevens
► Referenties
[1] ID Ivanovic. Geometrische beschrijving van de bepaling van de kwantumtoestand. Journal of Physics A: Mathematisch en algemeen, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kwantumcryptografie: Distributie van openbare sleutels en opgooien van munten. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Kwantumcryptografie gebaseerd op de stelling van Bell. Fysiek. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruß. Optimaal afluisteren in kwantumcryptografie met zes toestanden. Fysiek. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques en Mohamed Bourennane. Kwantum willekeurige toegangscodes met behulp van systemen met enkelvoudige $d$-niveaus. Fysiek. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas en Jędrzej Kaniewski. Zelftestende wederzijds onbevooroordeelde bases in het voorbereidings-en-meetscenario. Fysiek. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci en N. Gisin. Bell-ongelijkheid voor qunits met binaire metingen. Kwantuminformatie. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos en Remigiusz Augusiak. Maximale non-lokaliteit van maximale verstrengeling en wederzijds onbevooroordeelde bases, en zelftesten van kwantumsystemen met twee qutrits. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal en Jędrzej Kaniewski. Wederzijds onbevooroordeelde bases en symmetrische, informatief complete metingen in Bell-experimenten. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson en Karol Życzkowski. Op wederzijds onbevooroordeelde grondslagen. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K. Wootters en Brian D. Fields. Optimale toestandsbepaling door onderling zuivere metingen. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan en Thomas Beth. Nieuwbouw van onderling onpartijdige bases in vierkante maatvoering. Kwantuminformatie. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Mihály Weiner. Een opening voor het maximale aantal onderling onpartijdige basen. Proc. Amer. Wiskunde. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Proefschrift, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep en Pawel Wocjan. Wederzijds onbevooroordeelde bases en orthogonale decomposities van Lie-algebra's. Kwantuminformatie. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley en Stefan Weigert. Wederzijds onpartijdige bases construeren in dimensie zes. Fysiek. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi en Mihály Weiner. Een algemeen Pauli-probleem en een oneindige familie van MUB-tripletten in dimensie 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, mei 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer en Afaq Tahir. Bewijs voor en tegen Zauners MUB-vermoeden in $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https://doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling en Sven Polak. Wederzijds onbevooroordeelde bases: polynoomoptimalisatie en symmetrie. 2021. doi:10.48550/arXiv.2111.05698.
https://doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej en Karol Życzkowski. Wederzijds onbevooroordeelde basen en Hadamard-matrices van orde zes. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü en Berthold-Georg Englert. Wederzijds onbevooroordeelde bases in zes dimensies: de vier verst verwijderde bases. Fysiek. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz en Marcin Pawłowski. Verbindingen tussen wederzijds onbevooroordeelde bases en kwantum willekeurige toegangscodes. Fysiek. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani en Stephanie Wehner. Bell niet-lokaliteit. Rev. Mod. Phys., 86:419–478, 2014. doi:10.1103/RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOZEK ApS. MOSEK Fusion API voor C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe en Kouhei Harada. Een primal-dual internal point-methode voor niet-lineaire semi-definitieve programmering. Wiskundig programmeren, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd en Lieven Vandenberghe. Convexe optimalisatie. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt en parlementslid Vecchi. Optimalisatie door gesimuleerd uitgloeien. Wetenschap, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller en Edward Teller. Vergelijking van toestandsberekeningen door snelle rekenmachines. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio en Antonio Acín. De reeks kwantumcorrelaties begrenzen. Fysiek. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Geciteerd door
Dit artikel is gepubliceerd in Quantum onder de Creative Commons Naamsvermelding 4.0 Internationaal (CC BY 4.0) licentie. Het auteursrecht blijft berusten bij de oorspronkelijke houders van auteursrechten, zoals de auteurs of hun instellingen.