Sammenslåing av felt, matematikere går langt på gamle problem | Quanta Magazine

Endringen av planene kom på en biltur. På en vakker dag i april i fjor, matematikerne Rachel Greenfeld og Sarah Peluse la ut fra hjemmeinstitusjonen, Institute for Advanced Study i Princeton, New Jersey, på vei til Rochester, New York, hvor begge skulle holde foredrag dagen etter.

De hadde slitt i nesten to år med en viktig formodning innen harmonisk analyse, feltet som studerer hvordan man bryter komplekse signaler fra hverandre i komponentfrekvensene deres. Sammen med en tredje samarbeidspartner, Marina Iliopoulou, de studerte en versjon av problemet der komponentfrekvensene er representert som punkter i et plan hvis avstander fra hverandre er relatert til heltall. De tre forskerne prøvde å vise at det ikke kunne være for mange av disse punktene, men så langt har alle teknikkene deres kommet til kort.

De så ut til å snurre på hjulene sine. Så fikk Peluse en tanke: Hva om de droppet det harmoniske analyseproblemet - midlertidig, selvfølgelig - og vendte oppmerksomheten mot sett med punkter der avstanden mellom to punkter er nøyaktig et heltall? Hvilke mulige strukturer kan slike sett ha? Matematikere har prøvd å forstå heltallsavstandssett siden antikken. Pythagoras trippel (som 3, 4 og 5) representerer for eksempel rettvinklede trekanter hvis tre toppunkter er heltallsavstander fra hverandre.

"I bilen, antar jeg fordi Rachel var fanget sammen med meg, tok jeg den opp," sa Peluse, som nå er professor ved University of Michigan. Ideen om å takle heltallsavstand setter elektrifisert Greenfeld.

Før de visste ordet av det, hadde de ikke begynt én retningsendring, men to.

"Vi sluttet faktisk å ta hensyn til hvor vi skulle og gikk ikke av motorveien," sa Peluse. "Vi skulle i motsatt retning fra Rochester i omtrent en time før vi la merke til det, fordi vi var så spente på regnestykket."

I 1945, Norman Anning og Paul Erdős beviste at et uendelig sett med punkter i planet som alle er heltallsavstander fra hverandre må ligge på en linje. For et begrenset sett med punkter er mulighetene litt mer varierte. Matematikere har konstruert store sett som ligger på enten en linje eller en sirkel, noen ganger med tre eller fire ekstra punkter som er utenfor hoveddraget. (Punktene i seg selv trenger ikke å ha heltallskoordinater - spørsmålet handler om avstandene mellom dem.)

Ingen har kommet opp med et stort sett med punkter med noen annen konfigurasjon, men ingen har bevist at andre konfigurasjoner er umulige. I løpet av de nesten 80 årene siden Anning og Erdős' resultat, har faget praktisk talt ikke sett noen fremgang - før nå.

Greenfeld, Iliopoulou og Peluse har beviste at alle punktene i et stort heltallsavstandssett - unntatt kanskje en sparsom håndfull ytterpunkter - må ligge på en enkelt linje eller sirkel. "Hvis du vil ha et stort sett der alle parvise avstander er heltall, så er sirkler og linjer de eneste spillerne," sa József Solymosi ved University of British Columbia. Han kalte resultatet deres en «fantastisk løsning».

Den nye tilnærmingen bruker ideer og teknikker fra tre forskjellige områder av matematikk: kombinatorikk, tallteori og algebraisk geometri. Denne sammenføyningen av forskjellige felt "kan være et virkelig psykologisk gjennombrudd," sa Terence tao, en matematiker ved University of California, Los Angeles.

Alex Iosevich, fra University of Rochester, er enig. "De la et veldig solid grunnlag for et veldig bredt sett med problemer," sa han. "Det er absolutt ingen tvil i mitt sinn om at dette kommer til å finne enda dypere applikasjoner."

Enkelhetens grenser

Innenfor et fly er det enkelt å velge et uendelig sett med punkter som alle er heltallsavstander fra hverandre – bare ta favorittlinjen din, forestill deg en talllinje lagt over den, og bruk noen eller alle punktene som tilsvarer hele tall. Men dette er den eneste måten å konstruere en uendelig heltallsavstand satt i flyet, slik Anning og Erdős innså i 1945. Så snart du har bare tre punkter som ikke alle er på samme linje, blir konfigurasjonen din så begrenset at det er umulig å legge til uendelig mange flere poeng.

Årsaken koker ned til enkel geometri. Tenk deg å starte med to punkter, A og B, som er et heltalls avstand fra hverandre. Hvis du vil legge til et tredje punkt, C, som er en heltallsavstand fra både A og B, men ikke ligger på linjen gjennom dem, vil de fleste punktene i flyet ikke fungere. De eneste levedyktige punktene lever på spesielle kurver kalt hyperbler som skjærer mellom A og B. Hvis A og B er for eksempel 4 enheter fra hverandre, så er det nøyaktig fire av disse hyperbelene. (En hyperbel har vanligvis to distinkte deler, så for eksempel danner de to røde kurvene i figuren under en enkelt hyperbel.)

Når du først har valgt C (som i dette eksemplet er 3 enheter fra A og 5 enheter fra B), har du knapt noen muligheter for å legge til flere poeng. Ethvert punkt du kan legge til må ligge på en av hyperbelene mellom A og B, eller på linjen som går gjennom dem. Men den må også ligge på en av hyperbelene mellom A og C, og en av hyperbelene mellom B og C (eller de tilsvarende linjene) - med andre ord, et nytt punkt kan bare plasseres der tre hyperbler eller linjer krysser hverandre (skjønt ikke alle skjæringspunkter vil fungere). Det er bare endelig mange av disse hyperbelene og linjene til å begynne med, og to hyperbler (eller linjer) kan krysse hverandre i maksimalt fire punkter. Så du ender opp med bare uendelig mange skjæringspunkter å velge mellom - du kan ikke bygge et uendelig sett.

Når det gjelder å forstå hvordan et begrenset sett med heltallsavstandspunkter faktisk ser ut, blir hyperbeltilnærmingen raskt uhåndterlig. Når du legger til poeng, må du kjempe med økende antall hyperbler. For eksempel, når settet ditt bare har 10 poeng, vil å legge til en 11. opprette 10 nye familier med hyperbler - alle de mellom det nye punktet ditt og hvert av punktene som allerede er i settet. "Du kan ikke legge til mange poeng, fordi du vil gå deg vill i alle disse hyperbelene og skjæringspunktene," sa Greenfeld.

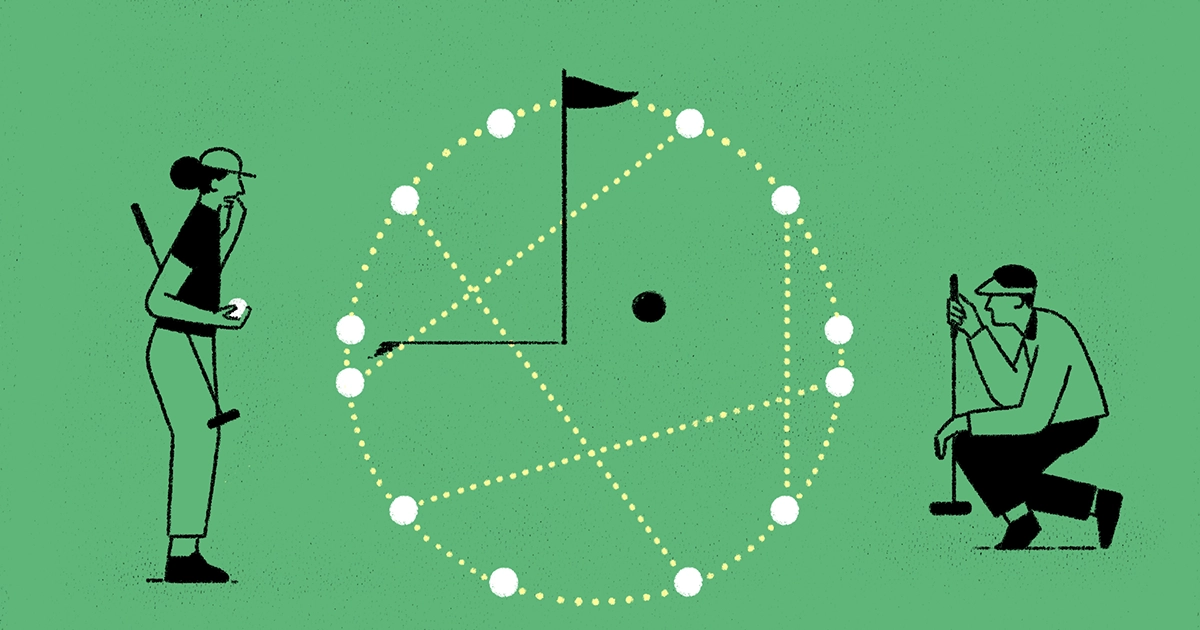
Så matematikere har sett etter mer håndterbare prinsipper for å konstruere store sett med heltallsavstandspunkter som ikke ligger på en linje. Men de har bare vært i stand til å komme opp med én tilnærming: Sett poengene dine på en sirkel. Hvis du vil ha en heltallsavstand satt med for eksempel en trillion poeng, er det måter å komme opp med en billion poeng på en sirkel med radius 1 hvis avstander fra hverandre er alle brøker. Deretter kan du blåse opp sirkelen til alle brøkavstandene blir til hele tall. Jo flere poeng du vil ha i settet ditt, jo mer trenger du for å blåse opp sirkelen.

Gjennom årene har matematikere kommet med bare litt mer eksotiske eksempler. De kan konstruere store heltallsavstandssett der alle unntatt fire punkter ligger på en linje eller alle unntatt tre ligger på en sirkel. Mange matematikere mistenker at dette er de eneste store heltallsavstandssettene der ikke alle punktene er på en linje eller en sirkel. De vil sikkert vite dette hvis de noen gang kan bevise noe som kalles Bombieri-Lang-formodningen. Men matematikere er delt om hvorvidt denne formodningen sannsynligvis er sann.

Siden Anning og Erdős arbeid i 1945, har matematikere gjort små fremskritt med å forstå heltallsavstandssett. Over tid syntes heltallsavstandsproblemet å slutte seg til en rekke andre problemer innen kombinatorikk, tallteori og geometri som er enkle å angi, men tilsynelatende umulige å løse. "Det er et mål på hvor patetisk matematikken vår er," sa Tao.

På en måte var heltallsavstandsproblemet et offer for sine egne tidlige suksesser. Hyperbelbeviset, med sin geniale enkelhet, er symbolsk for filosofien forfektet av Erdős, en svært innflytelsesrik matematiker som ofte snakket om "The Book" - et forestilt bind av de mest elegante bevisene i matematikk. Enkelhetskulturen Erdős fremmet har ført til "enorme resultater" i kombinatorisk geometri, sa Iosevich. Men det kan også føre til blinde flekker - i dette tilfellet om verdien av å bringe inn tilnærminger fra algebraisk geometri.

"Jeg tror ikke du vil finne et resultat [i algebraisk geometri] bevist de siste 50 årene som ikke er veldig teknisk involvert og rotete," sa Iosevich. "Men noen ganger må ting være slik."

I ettertid ventet heltallsavstandsproblemet på matematikere som var villige til å vurdere mer uregjerlige kurver enn hyperbler og deretter trekke på rekondittverktøy fra algebraisk geometri og tallteori for å temme dem. "Det krevde folk med tilstrekkelig bredde av kunnskap og interesse," sa Iosevich.

De fleste matematikere, sa han, er fornøyd med å bruke noen få verktøy i det ene hjørnet av matematikken gjennom hele karrieren. Men Greenfeld, Iliopoulou og Peluse er fryktløse oppdagere, sa Iosevich. "De ser på matematikk som en sammenhengende helhet."

Kompleksiserer problemet

Sommeren 2021 bestemte Greenfeld seg for at det var på tide å ta et stikk på et problem fra harmonisk analyse hun hadde fundert over siden forskerskolen. Klassisk harmonisk analyse, som danner grunnlaget for signalbehandling i den virkelige verden, handler om å dekomponere signaler til sinusbølger med forskjellige frekvenser og faser. Denne prosessen fungerer fordi det er mulig å lage en uendelig liste over sinusbølger som, når de kombineres, fanger opp alle funksjonene til ethvert signal, uten redundans.

Men ofte ønsker forskere å studere noe mer komplisert enn et endimensjonalt signal. For eksempel vil de kanskje dekomponere et signal på en disk i flyet. Men disken kan bare være vert for en begrenset samling av kompatible sinusbølger - for få til å fange oppførselen til alle mulige signaler på disken. Spørsmålet blir da: Hvor stor kan denne begrensede samlingen bli?

I en slik samling kan frekvensene til sinusene representeres som punkter i planet som virker uvillige til å gruppere seg i linjer og sirkler: Du vil aldri finne tre punkter som alle er nær samme linje, eller fire som alle er nærme til samme sirkel. Greenfeld håpet å bruke denne aversjonen til å bevise at disse settene med frekvenser bare kan inneholde noen få punkter.

På et møte i 2021 ved Universitetet i Bonn deltok Greenfeld på en tale om "determinantmetoden", en teknikk fra tallteori som kan brukes til å estimere hvor mange heltallspunkter av visse typer som kan ligge på kurver. Dette verktøyet, innså hun, kan være akkurat det hun trengte. Greenfeld rekrutterte Iliopoulou og Peluse, som også var på møtet. "Vi begynte å lære denne metoden sammen," sa Greenfeld.

Men til tross for mange anstrengelser, klarte de ikke å bøye den bestemmende metoden til deres formål, og våren 2023 følte de seg motløse. Iosevich hadde invitert Greenfeld og Peluse til å kjøre til Rochester for et besøk. "Så vi tenkte: 'OK, vi drar til Rochester, og å snakke med Alex vil gi oss nytt liv," sa Peluse. Men som det viste seg, landet de i Rochester allerede gjenopplivet, takket være en oppmuntrende diskusjon om heltallsavstandssett på deres uplanlagte omvei langs Susquehanna-elven i Pennsylvania.

De kom for sent til en planlagt middag med Iosevich, men de fant ham ventende i hotellets lobby med poser med takeaway. Han tilga at de var forsinket - og var mer enn tilgivende neste morgen, da de fortalte ham om planen deres om å takle heltallsavstandssett. "Han var så spent," husket Peluse. "Følelsesmessig var dette et stort løft."

Som med hyperbeltilnærmingen prøvde Greenfeld, Iliopoulou og Peluse å kontrollere strukturen til heltallsavstandssett ved å identifisere familier av kurver punktene må ligge på. Hyperbelmetoden begynner å bli for kronglete så snart du har mer enn noen få punkter, men Greenfeld, Iliopoulou og Peluse fant ut hvordan de kunne vurdere mange punkter samtidig ved å flytte hele konfigurasjonen inn i et høyere dimensjonalt rom.

For å se hvordan dette fungerer, anta at du starter med et "referanse" punkt A i heltallsavstandssettet. Annenhvert punkt i settet er en heltallsavstand fra A. Punktene lever i et plan, men du kan støte planet inn i tredimensjonalt rom ved å slå en tredje koordinat på hvert punkt, hvis verdi er avstanden fra A. For eksempel , anta at A er punktet (1, 3). Så blir punktet (4, 7), som er 5 enheter unna A, til punktet (4, 7, 5) i tredimensjonalt rom. Denne prosessen konverterer planet til en kjegle i tredimensjonalt rom hvis spissen sitter ved A, nå merket (1, 3, 0). Heltallsavstandspunktene blir punkter i tredimensjonalt rom som ligger på kjeglen og også på et visst gitter.

På samme måte, hvis du velger to referansepunkter, A og B, kan du konvertere punkter i planet til punkter i firedimensjonalt rom - bare gi hvert punkt to nye koordinater hvis verdier er avstandene til A og B. Denne prosessen konverterer planet inn i en buet overflate i firedimensjonalt rom. Du kan fortsette å legge til flere referansepunkter på denne måten. For hvert nytt referansepunkt øker dimensjonen med én og flyet blir kartlagt til en enda mer svingete overflate (eller, som matematikere sier, en overflate av høyere grad).

Med dette rammeverket på plass brukte forskerne determinantmetoden fra tallteori. Determinanter er tall, vanligvis assosiert med matriser, som fanger opp en rekke geometriske egenskaper til en samling av punkter - for eksempel kan en bestemt determinant måle arealet av trekanten dannet av tre av punktene. Determinantmetoden tilbyr en måte å bruke slike determinanter for å estimere antall punkter som ligger samtidig på en svingete overflate og på et gitter - akkurat den typen situasjon Greenfeld, Iliopoulou og Peluse hadde å gjøre med.

Forskerne brukte en arbeidslinje basert på determinantmetoden for å vise at når de støter heltallsavstanden opp til en passende høy dimensjon, må alle punktene ligge på et lite antall spesielle kurver. Disse kurvene, når deres skygger i planet ikke er en linje eller en sirkel, kan ikke inneholde mange gitterpunkter, som er de eneste kandidatene for punkter i heltallsavstandssettet. Det betyr at antall punkter i settet som kan ligge utenfor hovedlinjen eller sirkelen er begrenset - forskerne viste at det må være mindre enn en veldig sakte voksende funksjon av settets diameter.

Grensen deres når ikke standarden til "fire punkter utenfor linjen eller tre punkter utenfor sirkelen"-formodningen som mange matematikere tror er sann for sett med store heltallsavstander. Likevel viser resultatet at "essensen av formodningen er sann," sa Jacob Fox fra Stanford University. Et fullstendig bevis på formodningen vil sannsynligvis kreve en ny tilførsel av nye ideer, sa matematikere.

Teamets høydimensjonale kodingsskjema er "ekstremt robust," sa Iosevich. "Det er ikke bare applikasjoner i prinsippet - det er applikasjoner som jeg allerede tenker på."

En applikasjon, håper Greenfeld, Iliopoulou og Peluse, vil være til deres opprinnelige harmoniske analyseproblem, som de tre nå vender tilbake til. Resultatet deres på heltallsavstandssett "kan være et springbrett mot det," sa Greenfeld.

Syntesen av kombinatorikk med algebraisk geometri som forskerne satte i gang vil ikke stoppe med heltallsavstandssett eller allierte problemer i harmonisk analyse, spådde Iosevich. "Jeg tror at det vi ser er et konseptuelt gjennombrudd," sa han. "Dette sender en melding til folk i begge felt om at dette er en veldig produktiv interaksjon."

Det sender også en melding om verdien av noen ganger å gjøre et problem mer komplisert, sa Tao. Matematikere streber vanligvis etter det motsatte, bemerket han. "Men dette er et eksempel hvor kompleksisering av problemet faktisk er det riktige grepet."

Fremskrittet har endret måten han tenker på høygraderskurver, sa han. "Noen ganger kan de være dine venner og ikke dine fiender."