W 1850, Thomasa Penyngtona Kirkmana, matematyk, kiedy nie wypełniał swoich głównych obowiązków jako wikariusz w kościele anglikańskim, opisał swój „problem uczennic”: „Piętnaście młodych kobiet w szkole wychodzi trzy w rzędzie przez siedem dni z rzędu: należy się zaaranżować je codziennie, aby nikt nie szedł dwa razy obok siebie”.
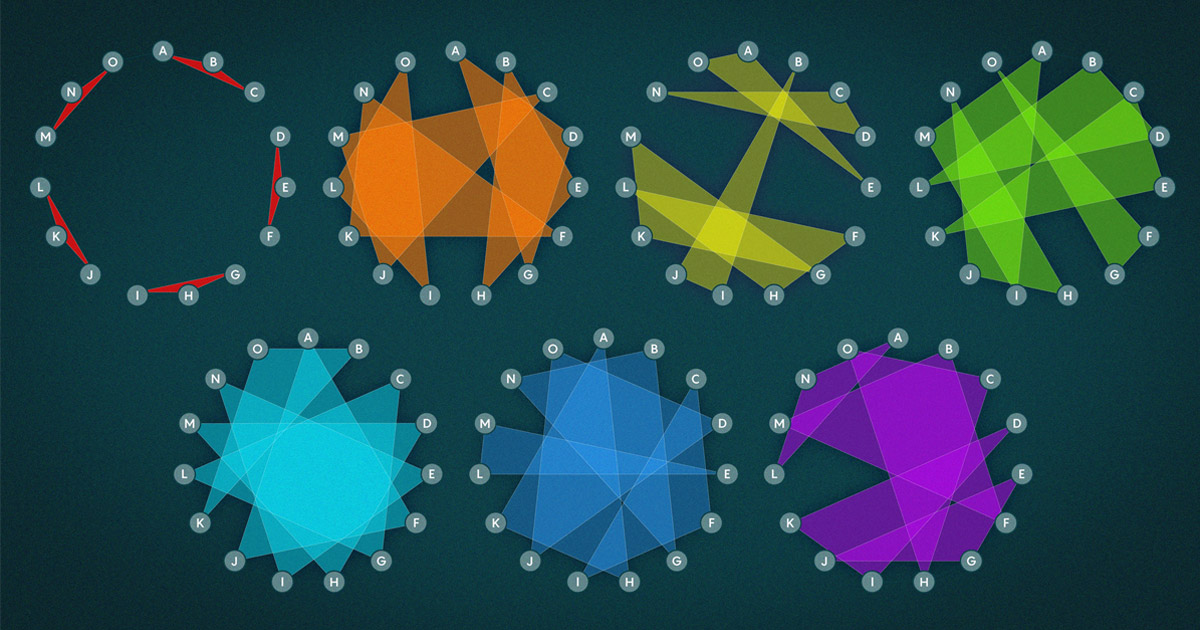
Współczesnemu matematykowi ten rodzaj problemu najlepiej wyobrazić sobie jako hipergraf — zbiór węzłów zebranych w grupy po trzy lub więcej. 15 uczennic to węzły, a każda grupa „trzy w rzędzie” może być traktowana jako trójkąt z trzema liniami lub krawędziami, łączącymi trzy węzły.
Problem Kirkmana zasadniczo polega na pytaniu, czy istnieje układ tych trójkątów, który łączy wszystkie uczennice ze sobą, ale z dodatkowym ograniczeniem, że żadne dwa trójkąty nie mają wspólnej krawędzi. Podział krawędzi oznaczałby, że dwie uczennice muszą iść razem więcej niż raz. To ograniczenie oznacza, że każda dziewczyna chodzi z dwoma nowymi przyjaciółmi codziennie przez tydzień, tak że każda możliwa para spotyka się dokładnie raz.
Ten problem i inne podobne omamiały matematyków przez prawie dwa stulecia, odkąd Kirkman postawił swoje pytanie. W 1973 r. legendarny matematyk Paul Erdős pozował podobny. Zapytał, czy możliwe jest zbudowanie hipergrafu o dwóch pozornie niekompatybilnych właściwościach. Po pierwsze, każda para węzłów musi być połączona dokładnie jednym trójkątem, tak jak w przypadku uczennic. Ta właściwość powoduje zagęszczenie wykresu trójkątami. Drugi wymóg wymusza bardzo precyzyjne rozłożenie trójkątów. (W szczególności wymaga to, aby dla każdej małej grupy trójkątów były co najmniej trzy węzły więcej niż trójkątów). Dawid Konon, matematyk z Kalifornijskiego Instytutu Technologii.
W styczniu tego roku skomplikowany 50-stronicowy dowód, czterech matematyków udowodniło, że zawsze można zbudować taki hipergraf, o ile masz wystarczającą liczbę węzłów. „Ilość szczegółów technicznych, przez które przeszli, tylko po to, aby to uzyskać, była niesamowita” – powiedział Allana Lo, matematyk na Uniwersytecie w Birmingham. Conlon zgodził się: „To naprawdę imponujące dzieło”.
Zespół badawczy zbudował system, który spełnił diabelskie wymagania Erdősa, rozpoczynając od losowego procesu wyboru trójkątów i zaprojektowanie go z niezwykłą starannością, tak aby odpowiadał ich potrzebom. „Liczba trudnych modyfikacji, które trafiają do dowodu, jest naprawdę oszałamiająca” – powiedział Conlon.
Ich strategia polegała na starannym zbudowaniu hipergrafu z poszczególnych trójkątów. Na przykład wyobraź sobie 15 naszych uczennic. Narysuj linię między każdą parą.
Celem jest tutaj wykreślenie trójkątów na tych liniach, tak aby trójkąty spełniały dwa wymagania: po pierwsze, żadne dwa trójkąty nie mają wspólnej krawędzi. (Systemy spełniające to wymaganie nazywane są systemami potrójnymi Steinera). Po drugie, upewnij się, że każdy mały podzbiór trójkątów wykorzystuje wystarczająco dużą liczbę węzłów.
Sposób, w jaki to zrobili badacze, najlepiej chyba zrozumieć za pomocą analogii.
Powiedzmy, że zamiast robić trójkąty z krawędzi, budujesz domy z klocków Lego. Pierwsze kilka budynków, które wykonujesz, jest ekstrawaganckich, ze wzmocnieniami konstrukcyjnymi i wyszukanymi zdobieniami. Kiedy już to zrobisz, odłóż je na bok. Będą służyć jako „pochłaniacz” — rodzaj uporządkowanego zapasu.
Teraz zacznij robić budynki z pozostałych cegieł, kontynuując bez większego planowania. Kiedy twoje zapasy Legos wyczerpią się, możesz znaleźć się z zabłąkanymi cegłami lub domami, które są niestabilne pod względem konstrukcyjnym. Ale ponieważ budynki z absorberami są tak przesadzone i wzmocnione, można tu i ówdzie wyrwać trochę cegieł i użyć ich bez narażania się na katastrofę.
W przypadku systemu potrójnego Steinera próbujesz stworzyć trójkąty. Twój absorber w tym przypadku to starannie dobrana kolekcja krawędzi. Jeśli nie możesz posortować reszty systemu w trójkąty, możesz użyć niektórych krawędzi prowadzących do absorbera. Następnie, kiedy już to zrobisz, sam absorber rozbijesz na trójkąty.
Absorpcja nie zawsze działa. Ale matematycy majstrowali przy tym procesie, znajdując nowe sposoby na omijanie przeszkód. Na przykład potężny wariant zwany absorpcją iteracyjną dzieli krawędzie na zagnieżdżoną sekwencję zestawów, tak że każdy z nich działa jak pochłaniacz dla następnego największego.
„W ciągu ostatniej dekady nastąpiła ogromna poprawa”, powiedział Conlon. „To coś w rodzaju formy sztuki, ale w tym momencie naprawdę przenieśli ją do poziomu sztuki wysokiej”.
Problem Erdősa był skomplikowany, nawet przy absorpcji iteracyjnej. „Dość szybko stało się jasne, dlaczego ten problem nie został rozwiązany”, powiedział Mehtaaba Sawhneya, jeden z czterech badaczy, którzy go rozwiązali, wraz z Ashwin Saha, który wraz z Sawhneyem jest absolwentem Massachusetts Institute of Technology; Michał Simkin, stypendysta podoktorski w Centrum Nauk Matematycznych i Zastosowań na Uniwersytecie Harvarda; oraz Mateusz Kwan, matematyk w Instytucie Nauki i Technologii Austria. „Były całkiem ciekawe, dość trudne zadania techniczne”.
Na przykład w innych zastosowaniach iteracyjnej absorpcji, gdy skończysz zajmować się zbiorem — albo trójkątami, dla potrójnych systemów Steinera, albo innymi strukturami dla innych problemów — możesz uznać, że został rozwiązany i o tym zapomnieć. Jednak warunki Erdősa uniemożliwiły czterem matematykom zrobienie tego. Problematyczne skupisko trójkątów może z łatwością obejmować węzły z wielu zestawów absorberów.
„Trójkąt, który wybrałeś 500 kroków temu, musisz jakoś zapamiętać, jak o tym myśleć” – powiedział Sawhney.
Cała czwórka w końcu zorientowała się, że jeśli starannie dobiorą swoje trójkąty, mogą obejść potrzebę śledzenia każdego drobiazgu. „Lepiej jest pomyśleć o dowolnym małym zestawie 100 trójkątów i zagwarantować, że zestaw trójkątów zostanie wybrany z odpowiednim prawdopodobieństwem”, powiedział Sawhney.
Autorzy nowego artykułu są optymistami, że ich technikę można rozszerzyć poza ten jeden problem. Oni mają już zastosowali swoją strategię do problemu o kwadraty łacińskie, które są jak uproszczenie układanki sudoku.
Poza tym istnieje kilka pytań, które mogą ostatecznie ustąpić metodom absorpcji, powiedział Kwan. „W kombinatoryce jest tak wiele problemów, zwłaszcza w teorii projektowania, gdzie procesy losowe są naprawdę potężnym narzędziem”. Jeden z takich problemów, przypuszczenie Rysera-Brualdi-Steina, dotyczy również kwadratów łacińskich i od lat 1960. czekał na rozwiązanie.
Chociaż absorpcja może wymagać dalszego rozwoju, zanim upora się z tym problemem, przeszła długą drogę od swojego powstania 30 temu, powiedział Maja Stein, zastępca dyrektora Centrum Modelowania Matematycznego na Uniwersytecie Chile. „Wspaniale jest zobaczyć, jak ewoluują te metody”.