Krzywa eliptyczna „szmerów” znaleziona dzięki sztucznej inteligencji w locie | Magazyn Quanta

Krzywe eliptyczne należą do najbardziej urzekających obiektów współczesnej matematyki. Nie wydają się skomplikowane, ale stanowią drogę ekspresową pomiędzy matematyką, której wiele osób uczy się w szkole średniej, a matematyką badawczą w jej najbardziej zawiłej formie. Odegrały one kluczową rolę w słynnym dowodzie Ostatniego Twierdzenia Fermata przeprowadzonym w latach 1990. przez Andrew Wilesa. Są kluczowymi narzędziami współczesnej kryptografii. W 2000 roku Instytut Matematyki Claya nazwał a domysły na temat statystyk krzywych eliptycznych, jeden z siedmiu „Problemów z Nagrodą Milenijną”, z których każdy za rozwiązanie otrzymuje nagrodę w wysokości 1 miliona dolarów. To przypuszczenie, na które po raz pierwszy odważył się Bryana Bircha i Petera Swinnertona-Dyera w latach sześćdziesiątych, nadal nie zostało udowodnione.

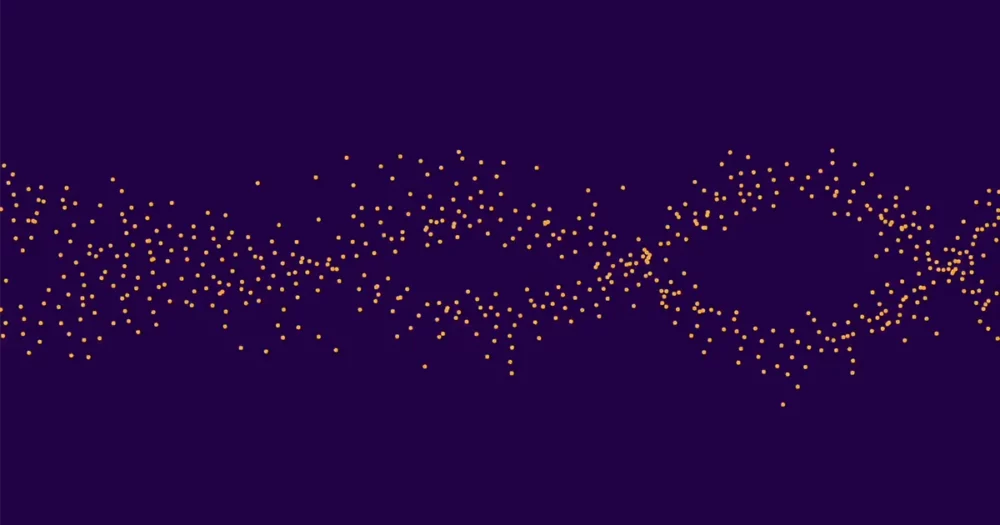
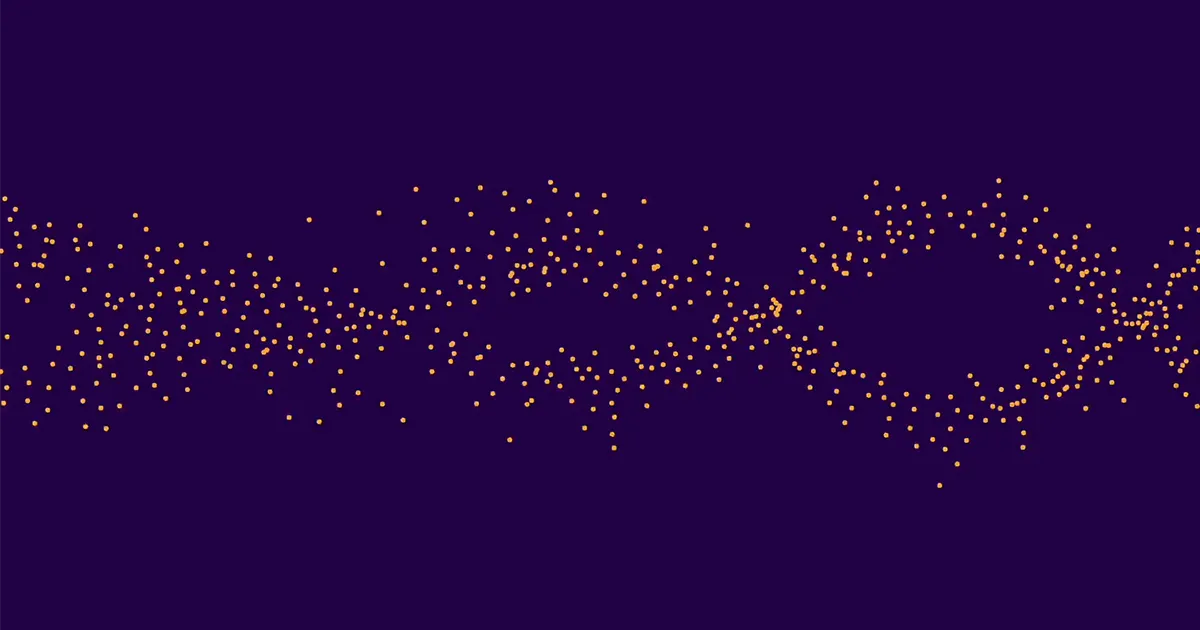
Zrozumienie krzywych eliptycznych to przedsięwzięcie wymagające dużej stawki, które ma kluczowe znaczenie w matematyce. Zatem kiedy w 2022 r. w ramach współpracy transatlantyckiej wykorzystano techniki statystyczne i sztuczną inteligencję do odkrycia zupełnie nieoczekiwanych wzorców na krzywych eliptycznych, był to mile widziany, choć nieoczekiwany wkład. „To była tylko kwestia czasu, zanim uczenie maszynowe wyląduje na naszym progu z czymś interesującym” – powiedział Piotr Sarnak, matematyk w Institute for Advanced Study i Princeton University. Początkowo nikt nie potrafił wyjaśnić, dlaczego istnieją nowo odkryte wzorce. Od tego czasu w serii niedawnych artykułów matematycy zaczęli odkrywać przyczyny powstawania wzorców, nazywanych „szmerami” ze względu na ich podobieństwo do płynnych kształtów gromadzących się szpaków, i zaczęli udowadniać, że muszą one występować nie tylko w określonych przykłady zbadane w 2022 r., ale bardziej ogólnie na krzywych eliptycznych.

Znaczenie bycia eliptycznym

Aby zrozumieć, czym są te wzorce, musimy trochę popracować nad tym, czym są krzywe eliptyczne i jak matematycy je kategoryzują.

Krzywa eliptyczna wiąże kwadrat jednej zmiennej, powszechnie zapisywany jako y, do trzeciej potęgi drugiej, powszechnie zapisywane jako x: y² = x³ + Ax + B, dla jakiejś pary liczb A i B, O ile A i B spełnić kilka prostych warunków. To równanie definiuje krzywą, którą można przedstawić na płaszczyźnie, jak pokazano poniżej. (Pomimo podobieństwa nazw elipsa nie jest krzywą eliptyczną.)

Choć pozornie proste, krzywe eliptyczne okazują się niezwykle potężnym narzędziem dla teoretyków liczb — matematyków szukających wzorców w liczbach całkowitych. Zamiast pozwalać zmiennym x i y obejmują wszystkie liczby, matematycy lubią ograniczać je do różnych systemów liczbowych, które nazywają definiowaniem krzywej „nad” danym systemem liczbowym. Szczególnie przydatne są krzywe eliptyczne ograniczone do liczb wymiernych — liczb, które można zapisać w postaci ułamków zwykłych. „Krzywe eliptyczne na liczbach rzeczywistych lub zespolonych są dość nudne” – powiedział Sarnak. „Głębokie są tylko liczby wymierne”.

Oto jeden ze sposobów, który jest prawdziwy. Jeśli narysujesz linię prostą pomiędzy dwoma wymiernymi punktami krzywej eliptycznej, miejsce, w którym ta linia ponownie przecina krzywą, również będzie wymierne. Możesz wykorzystać ten fakt do zdefiniowania „dodawania” na krzywej eliptycznej, jak pokazano poniżej.

Narysuj linię pomiędzy P i Q. Ta linia przetnie krzywą w trzecim punkcie, R. (Matematycy mają specjalny trik, aby poradzić sobie z przypadkiem, w którym linia nie przecina krzywej, dodając „punkt w nieskończoności.”) Odbicie R w poprzek x-oś to Twoja suma P + Q. Razem z tą operacją dodawania wszystkie rozwiązania krzywej tworzą obiekt matematyczny zwany grupą.

Matematycy używają tego do określenia „rankingu” krzywej. The ranga krzywej odnosi się do liczby racjonalnych rozwiązań, jakie posiada. Krzywe stopnia 0 mają skończoną liczbę rozwiązań. Krzywe o wyższym rzędzie mają nieskończoną liczbę rozwiązań, których wzajemne powiązanie za pomocą operacji dodawania opisuje stopień.

Rangi nie są dobrze rozumiane; matematycy nie zawsze potrafią je obliczyć i nie wiedzą, jak duże mogą być. (Największa znana dokładna ranga dla określonej krzywej to 20.) Podobnie wyglądające krzywe mogą mieć zupełnie różne rangi.

Krzywe eliptyczne mają również wiele wspólnego z liczbami pierwszymi, które dzielą się tylko przez 1 i same siebie. W szczególności matematycy przyglądają się krzywym ciał skończonych — systemom arytmetyki cyklicznej zdefiniowanym dla każdej liczby pierwszej. Pole skończone jest jak zegar z liczbą godzin równą liczbie pierwszej: jeśli będziesz odliczać w górę, liczby zaczną się od nowa. Na przykład w polu skończonym dla liczby 7 5 plus 2 równa się zero, a 5 plus 3 równa się 1.

Krzywa eliptyczna ma powiązaną sekwencję liczb, zwaną a_p, co odnosi się do liczby rozwiązań krzywej w ciele skończonym określonym przez liczbę pierwszą p. Mniejszy a_p oznacza więcej rozwiązań; większy a_p oznacza mniej rozwiązań. Chociaż trudno jest obliczyć rangę, kolejność a_p jest o wiele prostsze.

Na podstawie licznych obliczeń przeprowadzonych na jednym z pierwszych komputerów Birch i Swinnerton-Dyer wysnuli hipotezę o związku pomiędzy rzędem krzywej eliptycznej a sekwencją a_p. Każdy, kto udowodni, że miał rację, może wygrać milion dolarów i matematyczną nieśmiertelność.

Pojawia się wzór niespodzianki

Po rozpoczęciu pandemii, Yang-Hui He, badacz w Londyńskim Instytucie Nauk Matematycznych, postanowił podjąć nowe wyzwania. Studiował fizykę w college'u i uzyskał doktorat z fizyki matematycznej w Massachusetts Institute of Technology. Jednak coraz bardziej interesował się teorią liczb i biorąc pod uwagę rosnące możliwości sztucznej inteligencji, pomyślał, że spróbuje swoich sił w wykorzystaniu sztucznej inteligencji jako narzędzia do znajdowania nieoczekiwanych wzorców w liczbach. (Już był za pomocą uczenia maszynowego klasyfikować Rozmaitości Calabiego-Yau, struktury matematyczne szeroko stosowane w teorii strun.)

W sierpniu 2020 r., w miarę pogłębiania się pandemii, Uniwersytet w Nottingham gościł go na konferencji rozmowa online. Był pesymistą co do swoich postępów i samej możliwości wykorzystania uczenia maszynowego do odkrycia nowej matematyki. „Jego narracja była taka, że ​​teoria liczb jest trudna, ponieważ w teorii liczb nie można uczyć się maszynowo” – powiedział Thomas Olivier . , , , , , , , , , , , , , , ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, matematyk z Uniwersytetu Westminster, który był na widowni. Jak wspomina: „Nie mogłem niczego znaleźć, bo nie byłem ekspertem. Nawet nie użyłem odpowiednich rzeczy, żeby się temu przyjrzeć.

Oliver i Kyu-Hwan Lee, matematyk z Uniwersytetu Connecticut, rozpoczął współpracę z He. „Postanowiliśmy to zrobić, aby dowiedzieć się, czym jest uczenie maszynowe, a nie poważnie studiować matematykę” – powiedział Oliver. „Ale szybko odkryliśmy, że wielu rzeczy można się nauczyć maszynowo”.

Oliver i Lee zasugerowali, aby zastosował swoje techniki do zbadania L-funkcje, nieskończone szeregi ściśle powiązane z krzywymi eliptycznymi w ciągu a_p. Mogliby skorzystać z internetowej bazy danych zawierającej krzywe eliptyczne i pokrewne L-funkcje tzw LMFDB do szkolenia klasyfikatorów uczenia maszynowego. W tamtym czasie baza danych zawierała nieco ponad 3 miliony krzywych eliptycznych nad wymiernymi. Do października 2020 r. już to zrobili papier z których korzystano z uzyskanych informacji L-funkcje przewidywania określonej właściwości krzywych eliptycznych. W listopadzie podzielili się inny papier którzy wykorzystali uczenie maszynowe do klasyfikacji innych obiektów w teorii liczb. W grudniu udało im się to zrobić przewidzieć szeregi krzywych eliptycznych z dużą dokładnością.

Nie byli jednak pewni, dlaczego ich algorytmy uczenia maszynowego działają tak dobrze. Lee zapytał swojego studenta Aleksieja Pozdnyakova, czy potrafi zrozumieć, co się dzieje. Tak się składa, że ​​LMFDB sortuje krzywe eliptyczne według wielkości zwanej przewodnikiem, która podsumowuje informacje o liczbach pierwszych, dla których krzywa nie zachowuje się dobrze. Zatem Pozdnyakov próbował jednocześnie przyjrzeć się dużej liczbie krzywych z podobnymi przewodnikami – powiedzmy, wszystkim krzywym z przewodnikami od 7,500 do 10,000 XNUMX.

Łącznie dało to około 10,000 0 krzywych. Około połowa z nich miała rangę 1, a połowa rangę XNUMX. (wyższe stopnie są niezwykle rzadkie). Następnie uśrednił wartości a_p dla wszystkich krzywych rangi 0, oddzielnie uśrednione a_p dla wszystkich krzywych rangi 1 i wykreślił wyniki. Dwa zestawy kropek utworzyły dwie odrębne, łatwo dostrzegalne fale. Dlatego klasyfikatory uczenia maszynowego były w stanie poprawnie ustalić szeregi poszczególnych krzywych.

„Na początku byłem po prostu szczęśliwy, że wykonałem zadanie” – powiedział Pozdniakow. „Ale Kyu-Hwan natychmiast zauważył, że ten wzór jest zaskakujący i wtedy stał się naprawdę ekscytujący”.

Lee i Oliver byli zachwyceni. „Aleksiej pokazał nam zdjęcie, a ja powiedziałem, że wygląda jak to, co robią ptaki” – powiedział Oliver. „A potem Kyu-Hwan sprawdził to i powiedział, że nazywa się to szmerem, a Yang powiedział, że powinniśmy zadzwonić do gazety:”Szmery krzywych eliptycznych. ""

Przesłali swoją pracę w kwietniu 2022 r. i przesłali ją garstce innych matematyków, nerwowo oczekując, że powiedzą im, że ich tak zwane „odkrycie” jest powszechnie znane. Oliver stwierdził, że związek był na tyle widoczny, że należało go zauważyć już dawno.

Niemal natychmiast preprint wzbudził zainteresowanie, zwłaszcza ze strony Andrzej Sutherland, pracownik naukowy w MIT i jeden z redaktorów naczelnych LMFDB. Sutherland zdał sobie sprawę, że 3 miliony krzywych eliptycznych nie wystarczą do jego celów. Chciał przyjrzeć się znacznie większym zakresom przewodów, aby zobaczyć, jak mocne są szmery. Wyciągnął dane z innego ogromnego repozytorium zawierającego około 150 milionów krzywych eliptycznych. Wciąż niezadowolony, pobrał dane z innego repozytorium zawierającego 300 milionów krzywych.

„Ale nawet to nie wystarczyło, więc obliczyłem nowy zestaw danych składający się z ponad miliarda krzywych eliptycznych i właśnie tego użyłem do obliczenia zdjęć o naprawdę wysokiej rozdzielczości” – powiedział Sutherland. Szmery pojawiały się niezależnie od tego, czy miał średnio ponad 15,000 XNUMX krzywych eliptycznych na raz, czy milion na raz. Kształt pozostał ten sam, nawet gdy patrzył na krzywe coraz większych liczb pierwszych, zjawisko zwane niezmiennością skali. Sutherland zdał sobie również sprawę, że szmery nie są charakterystyczne tylko dla krzywych eliptycznych, ale pojawiają się także bardziej ogólnie L-Funkcje. On napisał list podsumowujący jego ustalenia i wysłał go do Sarnaka i Michała Rubinsteina na Uniwersytecie Waterloo.

„Jeśli istnieje znane wyjaśnienie tego zjawiska, spodziewam się, że je poznasz” – napisał Sutherland.

Nie zrobili tego.

Wyjaśnienie wzoru

Lee, He i Oliver zorganizowali warsztaty na temat szmerów w sierpniu 2023 r. w Instytucie Badań Obliczeniowych i Eksperymentalnych w Matematyce (ICERM) Uniwersytetu Browna. Przyszli Sarnak i Rubinstein, a także uczeń Sarnaka Nina Zubrilina.

Zubrilina przedstawiła swoje badania dotyczące wzorców szmerów w: formy modułowe, specjalne złożone funkcje, które, podobnie jak krzywe eliptyczne, są powiązane L-Funkcje. W modułowych formach z dużymi przewodnikami szmery zbiegają się w ostro zarysowaną krzywiznę, a nie tworzą dostrzegalny, ale rozproszony wzór. W papier opublikowane 11 października 2023 r. Zubrilina udowodniła, że ​​tego typu szmerowanie wynika z odkrytej przez nią wyraźnej formuły.

„Wielkim osiągnięciem Niny jest to, że otrzymała na to przepis; Nazywam to wzorem na gęstość szmerów Zubriliny” – powiedział Sarnak. „Korzystając z bardzo wyrafinowanej matematyki, udowodniła dokładny wzór, który idealnie pasuje do danych”.

Jej wzór jest skomplikowany, ale Sarnak uważa go za ważny nowy rodzaj funkcji, porównywalny z funkcjami Airy'ego, które definiują rozwiązania równań różniczkowych stosowanych w różnych kontekstach fizyki, od optyki po mechanikę kwantową.

Choć przepis Zubriliny był pierwszy, poszły w jego ślady inne. „Teraz co tydzień ukazuje się nowy artykuł” – powiedział Sarnak – „głównie wykorzystujący narzędzia Zubriliny i wyjaśniający inne aspekty szmerów”.

Jonathana Bobera, Andrzej Boker i Min lee Uniwersytetu w Bristolu wraz z Davida Lowry-Dudy ICERM, udowodnili istnienie innego typu szmerów w formach modułowych w kolejny październikowy artykuł. Oraz Kyu-Hwan Lee, Oliver i Pozdnyakov udowodnił istnienie szmerów w obiektach zwanych postaciami Dirichleta, z którymi są blisko spokrewnione L-Funkcje.

Sutherland był pod wrażeniem znacznej dawki szczęścia, która doprowadziła do odkrycia szmerów. Gdyby konduktor nie zamówił danych dotyczących krzywej eliptycznej, szmery zniknęłyby. „Mieli szczęście, że pobierali dane z LMFDB, które zostały wstępnie posortowane według konduktora” – powiedział. „To właśnie łączy krzywą eliptyczną z odpowiednią formą modułową, ale nie jest to wcale oczywiste. … Dwie krzywe, których równania wyglądają bardzo podobnie, mogą mieć bardzo różne przewodniki.” Zauważył to na przykład Sutherland y² = x³ - 11x + 6 ma przewodnika 17, ale zamiana znaku minus na znak plus, y² = x³ + 11x + 6 ma przewodnika 100,736 XNUMX.

Nawet wtedy szmery wykryto jedynie z powodu braku doświadczenia Pozdniakowa. „Nie sądzę, że bez niego znaleźlibyśmy to” – powiedział Oliver – „ponieważ eksperci tradycyjnie normalizują a_p mieć wartość bezwzględną 1. Ale ich nie znormalizował… więc oscylacje były bardzo duże i widoczne.

Wzorce statystyczne wykorzystywane przez algorytmy sztucznej inteligencji do sortowania krzywych eliptycznych według rang istnieją w przestrzeni parametrów o setkach wymiarów – zbyt wielu, aby ludzie mogli je posortować w myślach, nie mówiąc już o wizualizacji, zauważył Oliver. Chociaż uczenie maszynowe odkryło ukryte oscylacje, „dopiero później zrozumieliśmy, że są to szmery”.

Nota wydawcy: Andrew Sutherland, Kyu-Hwan Lee oraz baza danych funkcji L i formularzy modułowych (LMFDB) otrzymały fundusze od Fundacji Simonsa, która finansuje także tę niezależną redakcyjnie publikację. Decyzje dotyczące finansowania Fundacji Simonsa nie mają wpływu na nasz zasięg. Więcej informacji jest dostępnych tutaj.