Flow Conditions For Continuous Variable Measurement-based Quantum Computing

Republished By Plato

Followers: 0

Flow conditions for continuous variable measurement-based quantum computing PlatoBlockchain Data Intelligence. Vertical Search. Ai.

Robert I. Booth^1,2 and Damian Markham^1,3

¹Sorbonne Université, CNRS, LIP6, 4 place Jussieu, F-75005 Paris, France
²LORIA CNRS, Inria Mocqua, Université de Lorraine, F-54000 Nancy, France
³JFLI, CNRS / National Institute of Informatics, University of Tokyo, Tokyo, Japan

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

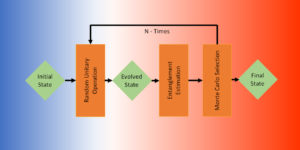
In measurement-based quantum computing (MBQC), computation is carried out by a sequence of measurements and corrections on an entangled state. Flow, and related concepts, are powerful techniques for characterising the dependence of the corrections on previous measurement results. We introduce flow-based methods for quantum computation with continuous-variable graph states, which we call CV-flow. These are inspired by, but not equivalent to, the notions of causal flow and g-flow for qubit MBQC. We also show that an MBQC with CV-flow approximates a unitary arbitrarily well in the infinite-squeezing limit, addressing issues of convergence which are unavoidable in the infinite-dimensional setting. In developing our proofs, we provide a method for converting a CV-MBQC computation into a circuit form, analogous to the circuit extraction method of Miyazaki et al, and an efficient algorithm for finding CV-flow when it exists based on the qubit version by Mhalla and Perdrix. Our results and techniques naturally extend to the cases of MBQC for quantum computation with qudits of prime local dimension.

► BibTeX data

@article{Booth2023flowconditions, doi = {10.22331/q-2023-10-19-1146}, url = {https://doi.org/10.22331/q-2023-10-19-1146}, title = {Flow conditions for continuous variable measurement-based quantum computing}, author = {Booth, Robert I. and Markham, Damian}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {7}, pages = {1146}, month = oct, year = {2023}<br /> }

► References

[1] Peter M. Albertiand Armin Uhlmann “On Bures Distance and *-Algebraic Transition Probability between Inner Derived Positive Linear Forms over W*-Algebras” Acta Applicandae Mathematica 60, 1-37 (2000).
https://doi.org/10.1023/A:1006317508252

[2] Rafael N. Alexanderand Nicolas C. Menicucci “Flexible Quantum Circuits Using Scalable Continuous-Variable Cluster States” Physical Review A 93, 062326 (2016).
https://doi.org/10.1103/PhysRevA.93.062326

[3] B. Antonio, D. Markham, and J. Anders, “Adiabatic Graph-State Quantum Computation” New Journal of Physics 16, 113070 (2014).
https://doi.org/10.1088/1367-2630/16/11/113070

[4] Warit Asavanant, Yu Shiozawa, Shota Yokoyama, Baramee Charoensombutamon, Hiroki Emura, Rafael N. Alexander, Shuntaro Takeda, Jun-ichi Yoshikawa, Nicolas C. Menicucci, Hidehiro Yonezawa, and Akira Furusawa, “Time-Domain Multiplexed 2-Dimensional Cluster State: Universal Quantum Computing Platform” Science 366, 373–376 (2019).
https://doi.org/10.1126/science.aay2645
arXiv:1903.03918

[5] Miriam Backens, Hector Miller-Bakewell, Giovanni de Felice, Leo Lobski, and John van de Wetering, “There and Back Again: A Circuit Extraction Tale” Quantum 5, 421 (2021).
https://doi.org/10.22331/q-2021-03-25-421

[6] Arno Bohmand Manuel Gadella “Dirac Kets, Gamow Vectors and Gel’fand Triplets” Springer Berlin, Heidelberg (1989).
https://doi.org/10.1007/3-540-51916-5

[7] Robert I. Booth, Aleks Kissinger, Damian Markham, Clément Meignant, and Simon Perdrix, “Outcome Determinism in Measurement-Based Quantum Computation with Qudits” (2021).
https://doi.org/10.48550/arXiv.2109.13810
arXiv:2109.13810

[8] Samuel L. Braunsteinand Peter van Loock “Quantum Information with Continuous Variables” Reviews of Modern Physics 77, 513–577 (2005).
https://doi.org/10.1103/RevModPhys.77.513

[9] Anne Broadbentand Elham Kashefi “Parallelizing Quantum Circuits” Theoretical Computer Science 410, 2489–2510 (2009).
https://doi.org/10.1016/j.tcs.2008.12.046

[10] D. E. Browne, E. Kashefi, M. Mhalla, and S. Perdrix, “Generalized Flow and Determinism in Measurement-based Quantum Computation” New Journal of Physics 9, 250–250 (2007).
https://doi.org/10.1088/1367-2630/9/8/250

[11] E. Celeghini, M. Gadella, and M. A. del Olmo, “Groups, Special Functions and Rigged Hilbert Spaces” Axioms 8 (2019).
https://doi.org/10.3390/axioms8030089
arXiv:1907.01281

[12] Vincent Danosand Elham Kashefi “Determinism in the One-Way Model” Physical Review A 74, 052310 (2006).
https://doi.org/10.1103/PhysRevA.74.052310

[13] Vincent Danos, Elham Kashefi, and Prakash Panangaden, “The Measurement Calculus” Journal of the ACM 54, 8–es (2007).
https://doi.org/10.1145/1219092.1219096

[14] Niel de Beaudrap “Finding Flows in the One-Way Measurement Model” Physical Review A 77, 022328 (2008).
https://doi.org/10.1103/PhysRevA.77.022328

[15] Niel de Beaudrap, Ross Duncan, Dominic Horsman, and Simon Perdrix, “Pauli Fusion: A Computational Model to Realise Quantum Transformations from ZX Terms” Electronic Proceedings in Theoretical Computer Science 318, 85–105 (2020).
https://doi.org/10.4204/EPTCS.318
arXiv:1904.12817

[16] Maurice A. de Gosson “Symplectic Geometry and Quantum Mechanics” Birkhäuser Basel (2006).
https://doi.org/10.1007/3-7643-7575-2

[17] Ross Duncan, Aleks Kissinger, Simon Perdrix, and John van de Wetering, “Graph-Theoretic Simplification of Quantum Circuits with the ZX-calculus” Quantum 4, 279 (2020).
https://doi.org/10.22331/q-2020-06-04-279
arXiv:1902.03178

[18] Ross Duncanand Simon Perdrix “Rewriting Measurement-Based Quantum Computations with Generalised Flow” Springer Berlin Heidelberg (2010).
https://doi.org/10.1007/978-3-642-14162-1_24

[19] J. Eisert, S. Scheel, and M. B. Plenio, “Distilling Gaussian States with Gaussian Operations Is Impossible” Physical Review Letters 89, 137903 (2002).
https://doi.org/10.1103/PhysRevLett.89.137903

[20] Claude Fabreand Nicolas Treps “Modes and States in Quantum Optics” Reviews of Modern Physics 92, 035005 (2020).
https://doi.org/10.1103/RevModPhys.92.035005
arXiv:1912.09321

[21] Joseph F. Fitzsimonsand Elham Kashefi “Unconditionally Verifiable Blind Quantum Computation” Physical Review A 96 (2017).
https://doi.org/10.1103/PhysRevA.96.012303

[22] M. Gadellaand F. Gómez “A Unified Mathematical Formalism for the Dirac Formulation of Quantum Mechanics” Foundations of Physics 32, 815–869 (2002).
https://doi.org/10.1023/A:1016069311589

[23] I. Gel’fandand G. Shilov “Generalized Functions, Volume 1: Properties and Operations” American Mathematical Society (2016).
https://doi.org/10.1090/chel/377
http://www.ams.org/chel/377

[24] I. Gel’fandand G. Shilov “Generalized Functions, Volume 2: Spaces of Fundamental and Generalized Functions” American Mathematical Society (2016).
https://doi.org/10.1090/chel/378
http://www.ams.org/chel/378

[25] I. Gel’fandand G. Shilov “Generalized Functions, Volume 3: Theory of Differential Equations” American Mathematical Society (2016).
https://doi.org/10.1090/chel/379
http://www.ams.org/chel/379

[26] I. Gel’fandand N. Ya Vilenkin “Generalized Functions, Volume 4: Applications of Harmonic Analysis” American Mathematical Society (2016).
https://doi.org/10.1090/chel/380
http://www.ams.org/chel/380

[27] Daniel Gottesman, Alexei Kitaev, and John Preskill, “Encoding a Qubit in an Oscillator” Physical Review A 64 (2001).
https://doi.org/10.1103/PhysRevA.64.012310

[28] Mile Gu, Christian Weedbrook, Nicolas C. Menicucci, Timothy C. Ralph, and Peter van Loock, “Quantum Computing with Continuous-Variable Clusters” Physical Review A 79 (2009).
https://doi.org/10.1103/PhysRevA.79.062318
arXiv:0903.3233

[29] Brian C. Hall “Quantum Theory for Mathematicians” Springer-Verlag (2013).
https://doi.org/10.1007/978-1-4614-7116-5

[30] Shuhong Hao, Meihong Wang, Dong Wang, and Xiaolong Su, “Topological Error Correction with a Gaussian Cluster State” Physical Review A 103, 052407 (2021).
https://doi.org/10.1103/PhysRevA.103.052407

[31] JinChuan Houand XiaoFei Qi “Fidelity of States in Infinite-Dimensional Quantum Systems” Science China Physics, Mechanics and Astronomy 55, 1820–1827 (2012).
https://doi.org/10.1007/s11433-012-4840-4

[32] Timjan Kalajdzievskiand Nicolás Quesada “Exact and Approximate Continuous-Variable Gate Decompositions” Quantum 5, 394 (2021).
https://doi.org/10.22331/q-2021-02-08-394

[33] Michael Keyl, Jukka Kiukas, and Reinhard F. Werner, “Schwartz Operators” Reviews in Mathematical Physics 28, 1630001 (2016).
https://doi.org/10.1142/S0129055X16300016
arXiv:1503.04086

[34] Shunya Konno, Warit Asavanant, Kosuke Fukui, Atsushi Sakaguchi, Fumiya Hanamura, Petr Marek, Radim Filip, Jun-ichi Yoshikawa, and Akira Furusawa, “Non-Clifford Gate on Optical Qubits by Nonlinear Feedforward” Physical Review Research 3, 043026 (2021).
https://doi.org/10.1103/PhysRevResearch.3.043026

[35] Shunya Konno, Atsushi Sakaguchi, Warit Asavanant, Hisashi Ogawa, Masaya Kobayashi, Petr Marek, Radim Filip, Jun-ichi Yoshikawa, and Akira Furusawa, “Nonlinear Squeezing for Measurement-Based Non-Gaussian Operations in Time Domain” Physical Review Applied 15, 024024 (2021).
https://doi.org/10.1103/PhysRevApplied.15.024024
arXiv:2011.14576

[36] Seth Lloydand Samuel L. Braunstein “Quantum Computation over Continuous Variables” Physical Review Letters 82, 1784–1787 (1999).
https://doi.org/10.1103/PhysRevLett.82.1784

[37] A. I. Lvovsky “Squeezed Light” John Wiley & Sons, Ltd chapter 5 (2015).
https://doi.org/10.1002/9781119009719.ch5

[38] Atul Mantri, Tommaso F. Demarie, Nicolas C. Menicucci, and Joseph F. Fitzsimons, “Flow Ambiguity: A Path Towards Classically Driven Blind Quantum Computation” Physical Review X 7 (2017).
https://doi.org/10.1103/PhysRevX.7.031004
arXiv:1608.04633

[39] Damian Markhamand Elham Kashefi “Entanglement, Flow and Classical Simulatability in Measurement Based Quantum Computation” Springer International Publishing (2014).
https://doi.org/10.1007/978-3-319-06880-0_22

[40] Nicolas C. Menicucci, Steven T. Flammia, and Peter van Loock, “Graphical Calculus for Gaussian Pure States” Physical Review A 83 (2011).
https://doi.org/10.1103/PhysRevA.83.042335
arXiv:1007.0725

[41] Nicolas C. Menicucci, Peter van Loock, Mile Gu, Christian Weedbrook, Timothy C. Ralph, and Michael A. Nielsen, “Universal Quantum Computation with Continuous-Variable Cluster States” Physical Review Letters 97 (2006).
https://doi.org/10.1103/PhysRevLett.97.110501

[42] Mehdi Mhalla, Mio Murao, Simon Perdrix, Masato Someya, and Peter S. Turner, “Which Graph States Are Useful for Quantum Information Processing?” Theory of Quantum Computation, Communication, and Cryptography 174–187 (2014).
https://doi.org/10.1007/978-3-642-54429-3_12

[43] Mehdi Mhallaand Simon Perdrix “Finding Optimal Flows Efficiently” Automata, Languages and Programming 857–868 (2008).
https://doi.org/10.1007/978-3-540-70575-8_70

[44] Kazunori Miyata, Hisashi Ogawa, Petr Marek, Radim Filip, Hidehiro Yonezawa, Jun-ichi Yoshikawa, and Akira Furusawa, “Implementation of a Quantum Cubic Gate by Adaptive Non-Gaussian Measurement” Physical Review A 93, 022301 (2016).
https://doi.org/10.1103/PhysRevA.93.022301
arXiv:1507.08782

[45] Jisho Miyazaki, Michal Hajdušek, and Mio Murao, “An Analysis of the Trade-off between Spatial and Temporal Resources for Measurement-Based Quantum Computation” Physical Review A 91, 052302 (2015).
https://doi.org/10.1103/PhysRevA.91.052302
arXiv:1310.4043

[46] Julien Niset, Jaromír Fiurášek, and Nicolas J. Cerf, “No-Go Theorem for Gaussian Quantum Error Correction” Physical Review Letters 102, 120501 (2009).
https://doi.org/10.1103/PhysRevLett.102.120501

[47] Kyungjoo Noh, S. M. Girvin, and Liang Jiang, “Encoding an Oscillator into Many Oscillators” Physical Review Letters 125, 080503 (2020).
https://doi.org/10.1103/PhysRevLett.125.080503
arXiv:1903.12615

[48] Stefano Pirandola, Riccardo Laurenza, and Samuel L. Braunstein, “Teleportation Simulation of Bosonic Gaussian Channels: Strong and Uniform Convergence” The European Physical Journal D 72, 162 (2018).
https://doi.org/10.1140/epjd/e2018-90253-1
arXiv:1712.01615

[49] Robert Raussendorfand Hans J. Briegel “A One-Way Quantum Computer” Physical Review Letters 86, 5188–5191 (2001).
https://doi.org/10.1103/PhysRevLett.86.5188

[50] Robert Raussendorfand Hans J. Briegel “Computational Model Underlying the One-Way Quantum Computer” Quantum Info. Comput. 2, 443–486 (2002).
https://doi.org/10.5555/2011492.2011495

[51] Adam Sawickiand Katarzyna Karnas “Universality of Single Qudit Gates” Annales Henri Poincaré 18, 3515–3552 (2017).
https://doi.org/10.1007/s00023-017-0604-z
arXiv:1609.05780

[52] Kunal Sharmaand Mark M. Wilde “Characterizing the Performance of Continuous-Variable Gaussian Quantum Gates” Physical Review Research 2, 013126 (2020).
https://doi.org/10.1103/PhysRevResearch.2.013126
arXiv:1810.12335

[53] M. E. Shirokovand A. S. Holevo “On Approximation of Infinite-Dimensional Quantum Channels” Problems of Information Transmission 44, 73–90 (2008).
https://doi.org/10.1134/S0032946008020014

[54] Armin Uhlmann “The “Transition Probability” in the State Space of a ${_ast}$-Algebra” Reports on Mathematical Physics 9, 273–279 (1976).
https://doi.org/10.1016/0034-4877(76)90060-4

[55] Christophe Vuillot, Hamed Asasi, Yang Wang, Leonid P. Pryadko, and Barbara M. Terhal, “Quantum Error Correction with the Toric-GKP Code” Physical Review A 99, 032344 (2019).
https://doi.org/10.1103/PhysRevA.99.032344
arXiv:1810.00047

[56] Richard L. Wheedenand Antoni Zygmund “Measure and Integral : An Introduction to Real Analysis, Second Edition” Chapman and Hall/CRC (2015).
https://doi.org/10.1201/b18361

[57] Mark M. Wilde “Strong and Uniform Convergence in the Teleportation Simulation of Bosonic Gaussian Channels” Physical Review A 97, 062305 (2018).
https://doi.org/10.1103/PhysRevA.97.062305
arXiv:1712.00145

[58] Shota Yokoyama, Ryuji Ukai, Seiji C. Armstrong, Chanond Sornphiphatphong, Toshiyuki Kaji, Shigenari Suzuki, Jun-ichi Yoshikawa, Hidehiro Yonezawa, Nicolas C. Menicucci, and Akira Furusawa, “Ultra-Large-Scale Continuous-Variable Cluster States Multiplexed in the Time Domain” Nature Photonics 7, 982–986 (2013).
https://doi.org/10.1038/nphoton.2013.287

[59] Jun-ichi Yoshikawa, Shota Yokoyama, Toshiyuki Kaji, Chanond Sornphiphatphong, Yu Shiozawa, Kenzo Makino, and Akira Furusawa, “Generation of One-Million-Mode Continuous-Variable Cluster State by Unlimited Time-Domain Multiplexing” APL Photonics 1, 060801 (2016).
https://doi.org/10.1063/1.4962732
arXiv:1606.06688

[60] Jing Zhang “Graphical Description of Local Gaussian Operations for Continuous-Variable Weighted Graph States” Physical Review A 78, 052307 (2008).
https://doi.org/10.1103/PhysRevA.78.052307
arXiv:0810.1343

[61] Jing Zhang “Graphical Rule of Transforming Continuous-Variable Graph States by Local Homodyne Detection” Physical Review A 82, 034303 (2010).
https://doi.org/10.1103/PhysRevA.82.034303
arXiv:1006.3974

[62] Jing Zhangand Samuel L. Braunstein “Continuous-Variable Gaussian Analog of Cluster States” Physical Review A 73 (2006).
https://doi.org/10.1103/PhysRevA.73.032318

[63] D. L. Zhou, B. Zeng, Z. Xu, and C. P. Sun, “Quantum Computation Based on D-Level Cluster States” Physical Review A 68, 062303 (2003).
https://doi.org/10.1103/PhysRevA.68.062303

Cited by

[1] Robert I. Booth, Aleks Kissinger, Damian Markham, Clément Meignant, and Simon Perdrix, “Outcome determinism in measurement-based quantum computation with qudits”, Journal of Physics A Mathematical General 56 11, 115303 (2023).

The above citations are from SAO/NASA ADS (last updated successfully 2023-10-19 11:48:25). The list may be incomplete as not all publishers provide suitable and complete citation data.

Could not fetch Crossref cited-by data during last attempt 2023-10-19 11:48:24: Could not fetch cited-by data for 10.22331/q-2023-10-19-1146 from Crossref. This is normal if the DOI was registered recently.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

SEO Powered Content & PR Distribution. Get Amplified Today.
PlatoData.Network Vertical Generative Ai. Empower Yourself. Access Here.
PlatoAiStream. Web3 Intelligence. Knowledge Amplified. Access Here.
PlatoESG. Carbon, CleanTech, Energy, Environment, Solar, Waste Management. Access Here.
PlatoHealth. Biotech and Clinical Trials Intelligence. Access Here.
Source: https://quantum-journal.org/papers/q-2023-10-19-1146/

Time Stamp: October 19, 2023

Time Stamp: May 4, 2023

Republished By Plato

Abstract

► BibTeX data

► References

Cited by

Automated Generation of Shuttling Sequences for a Linear Segmented Ion Trap Quantum Computer

Neural Network Approach to the Simulation of Entangled States with One Bit of Communication

Unifying different notions of quantum incompatibility into a strict hierarchy of resource theories of communication

Pipelined correlated minimum weight perfect matching of the surface code

The quantum switch is uniquely defined by its action on unitary operations

Quantum key distribution rates from semidefinite programming

Periodically refreshed quantum thermal machines

Towards Quantum Advantage in Financial Market Risk using Quantum Gradient Algorithms

Generation of highly retrievable atom photon entanglement with a millisecond lifetime via a spatially multiplexed cavity

Measurement optimization of variational quantum simulation by classical shadow and derandomization

About Us

Vertical Search & Ai

Platform

Stay Connected

Account