Improving social welfare in non-cooperative games with different types of quantum resources

Improving social welfare in non-cooperative games with different types of quantum resources

Time Stamp: June 17, 2024 10:42 AM

Alastair A. Abbott1, Mehdi Mhalla2, and Pierre Pocreau1,2

1Univ. Grenoble Alpes, Inria, 38000 Grenoble, France
2Univ. Grenoble Alpes, CNRS, Grenoble INP, LIG, 38000 Grenoble, France

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

We investigate what quantum advantages can be obtained in multipartite non-cooperative games by studying how different types of quantum resources can lead to new Nash equilibria and improve social welfare — a measure of the quality of an equilibrium. Two different quantum settings are analysed: a first, in which players are given direct access to an entangled quantum state, and a second, which we introduce here, in which they are only given classical advice obtained from quantum devices. For a given game $G$, these two settings give rise to different equilibria characterised by the sets of equilibrium correlations $Q_textrm{corr}(G)$ and $Q(G)$, respectively. We show that $Q(G)subseteq Q_textrm{corr}(G)$, and by exploiting the self-testing property of some correlations, that the inclusion is strict for some games $G$. We make use of SDP optimisation techniques to study how these quantum resources can improve social welfare, obtaining upper and lower bounds on the social welfare reachable in each setting. We investigate, for several games involving conflicting interests, how the social welfare depends on the bias of the game and improve upon a separation that was previously obtained using pseudo-telepathic solutions.

Improving social welfare in non-cooperative games with different types of quantum resources PlatoBlockchain Data Intelligence. Vertical Search. Ai.

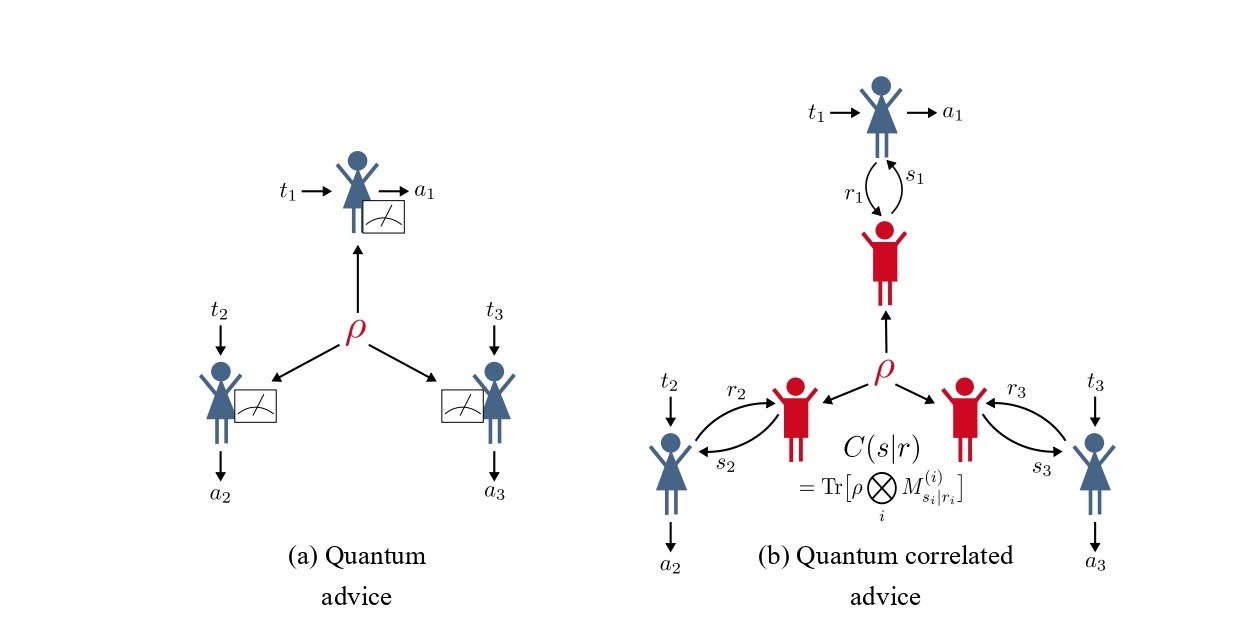
Featured image: The two quantum scenarios we consider. (a) “Quantum advice”: direct access to a shared quantum state. (b) “Quantum correlated advice”: classical access to a quantum correlation $C(s|r)$ via several local mediators sharing an entangled quantum state.

Popular summary

One of the most striking phenomena in quantum mechanics is the possibility for spatially separated parties to generate, without communicating, correlations that cannot be explained by classical physics. This phenomenon can be captured in games where several spatially separated parties try to coordinate and answer questions asked by a referee, upon which they receive a payout when they answer correctly. When the players are not allowed to communicate, having access to quantum resources can help them to coordinate better than they could with classical resources, leading to a better average payout, a quantity known as their “social welfare”. In this work, we study the case of conflicting interest games, in which players’ interests are not aligned. In such games, one is interested in stable behaviour, in which no player can individually increase their payout by changing their strategy. Such strategies correspond to the famous notion of Nash equilibria.

We study how quantum resources, such as entanglement, can help the players achieve Nash equilibria with better social welfare than using classical resources. We make a novel distinction between two different types of quantum resources: one in which the players have full control of a quantum device to perform measurements, and another in which they only have indirect, classical access to a quantum device they are provided with. Surprisingly, we find that this latter, classical access to quantum devices actually allows the players to reach more Nash equilibria. Numerical simulations indicate that some of these additional equilibria achieve higher social welfare for the players.

► BibTeX data

► References

[1] John F. Nash. “Equilibrium points in $n$-person games”. Proceedings of the National Academy of Sciences 36, 48–49 (1950).
https:/​/​doi.org/​10.1073/​pnas.36.1.48

[2] Roger B. Myerson. “Nash equilibrium and the history of economic theory”. Journal of Economic Literature 37, 1067–1082 (1999).
https:/​/​doi.org/​10.1257/​jel.37.3.1067

[3] Jorma Jormakka and Jarmo V. E. Mölsä. “Modelling information warfare as a game”. Journal of Information Warfare 4, 12–25 (2005). url: https:/​/​www.jstor.org/​stable/​26504060.
https:/​/​www.jstor.org/​stable/​26504060

[4] Robert Gibbons. “Game theory for applied economists”. Princeton University Press. Princeton, NJ, USA (1992).
https:/​/​doi.org/​10.2307/​j.ctvcmxrzd

[5] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani, and Stephanie Wehner. “Bell nonlocality”. Reviews of Modern Physics 86, 419 (2014).
https:/​/​doi.org/​10.1103/​RevModPhys.86.419

[6] Vincenzo Auletta, Diodato Ferraioli, Ashutosh Rai, Giannicola Scarpa, and Andreas Winter. “Belief-invariant and quantum equilibria in games of incomplete information”. Theoretical Computer Science 895, 151–177 (2021).
https:/​/​doi.org/​10.1016/​j.tcs.2021.09.041

[7] Ryszard Horodecki, Pawel Horodecki, Michal Horodecki, and Karol Horodecki. “Quantum entanglement”. Reviews of Modern Physics 81, 865 (2009).
https:/​/​doi.org/​10.1103/​RevModPhys.81.865

[8] Katarzyna Bolonek-Lasoń. “Three-player conflicting interest games and nonlocality”. Quantum Information Processing 16, 186 (2017).
https:/​/​doi.org/​10.1007/​s11128-017-1635-6

[9] Berry Groisman, Michael Mc Gettrick, Mehdi Mhalla, and Marcin Pawłowski. “How quantum information can improve social welfare”. IEEE Journal on Selected Areas in Information Theory 1, 445–453 (2020).
https:/​/​doi.org/​10.1109/​JSAIT.2020.3012922

[10] Robert J. Aumann. “Subjectivity and correlation in randomized strategies”. Journal of Mathematical Economics 1, 67–96 (1974).
https:/​/​doi.org/​10.1016/​0304-4068(74)90037-8

[11] Françoise Forges. “Correlated equilibrium in games with incomplete information revisited”. Theory and Decision 61, 329–344 (2006).
https:/​/​doi.org/​10.1007/​s11238-006-9005-3

[12] Ehud Lehrer, Dinah Rosenberg, and Eran Shmaya. “Signaling and mediation in games with common interests”. Games and Economic Behavior 68, 670–682 (2010).
https:/​/​doi.org/​10.1016/​j.geb.2009.08.007

[13] Ivan Šupić and Joseph Bowles. “Self-testing of quantum systems: a review”. Quantum 4, 337 (2020).
https:/​/​doi.org/​10.22331/​q-2020-09-30-337

[14] Anurag Anshu, Peter Høyer, Mehdi Mhalla, and Simon Perdrix. “Contextuality in multipartite pseudo-telepathy graph games”. Journal of Computer and System Sciences 107, 156–165 (2020).
https:/​/​doi.org/​10.1016/​j.jcss.2019.06.005

[15] Mamoru Kaneko and Kenjiro Nakamura. “The Nash social welfare function”. Econometrica 47, 423–435 (1979).
https:/​/​doi.org/​10.2307/​1914191

[16] Yael Tauman Kalai, Ran Raz, and Ron D. Rothblum. “How to delegate computations: the power of no-signaling proofs”. In Proceedings of the forty-sixth annual ACM symposium on Theory of computing. Pages 485–494. New York, NY, USA (2014). Association for Computing Machinery.
https:/​/​doi.org/​10.1145/​2591796.2591809

[17] Lluis Masanes, Antonio Acín, and Nicolas Gisin. “General properties of nonsignaling theories”. Physical Review A 73, 012112 (2006).
https:/​/​doi.org/​10.1103/​PhysRevA.73.012112

[18] Pierfrancesco La Mura. “Correlated equilibria of classical strategic games with quantum signals”. International Journal of Quantum Information 03, 183–188 (2005).
https:/​/​doi.org/​10.1142/​S0219749905000724

[19] Shengyu Zhang. “Quantum strategic game theory”. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference. Pages 39–59. New York, NY, USA (2012). Association for Computing Machinery.
https:/​/​doi.org/​10.1145/​2090236.2090241

[20] Anna Pappa, Niraj Kumar, Thomas Lawson, Miklos Santha, Shengyu Zhang, Eleni Diamanti, and Iordanis Kerenidis. “Nonlocality and conflicting interest games”. Physical Review Letters 114, 020401 (2015).
https:/​/​doi.org/​10.1103/​PhysRevLett.114.020401

[21] John Bostanci and John Watrous. “Quantum game theory and the complexity of approximating quantum Nash equilibria”. Quantum 6, 882 (2022).
https:/​/​doi.org/​10.22331/​q-2022-12-22-882

[22] Faisal Shah Khan, Neal Solmeyer, Radhakrishnan Balu, and Travis S Humble. “Quantum games: a review of the history, current state, and interpretation”. Quantum Information Processing 17, 1–42 (2018).
https:/​/​doi.org/​10.1007/​s11128-018-2082-8

[23] Antonio Acín, Nicolas Brunner, Nicolas Gisin, Serge Massar, Stefano Pironio, and Valerio Scarani. “Device-independent security of quantum cryptography against collective attacks”. Physical Review Letters 98, 230501 (2007).
https:/​/​doi.org/​10.1103/​PhysRevLett.98.230501

[24] Anne Broadbent, Joseph Fitzsimons, and Elham Kashefi. “Universal blind quantum computation”. In 2009 50th Annual IEEE Symposium on Foundations of Computer Science. Pages 517–526. Atlanta, GA, USA (2009). IEEE.
https:/​/​doi.org/​10.1109/​FOCS.2009.36

[25] Gilles Brassard, Anne Broadbent, and Alain Tapp. “Quantum pseudo-telepathy”. Foundations of Physics 35, 1877–1907 (2005).
https:/​/​doi.org/​10.1007/​s10701-005-7353-4

[26] Daniel M. Greenberger, Michael A. Horne, and Anton Zeilinger. “Going beyond Bell’s theorem”. Pages 69–72. Springer. Dordrecht, Netherlands (1989).
https:/​/​doi.org/​10.1007/​978-94-017-0849-4_10

[27] Flavio Baccari, Remigiusz Augusiak, Ivan Šupić, Jordi Tura, and Antonio Acín. “Scalable Bell inequalities for qubit graph states and robust self-testing”. Physical Review Letters 124, 020402 (2020).
https:/​/​doi.org/​10.1103/​PhysRevLett.124.020402

[28] Laura Mančinska. Private communication (2023).

[29] Nicolas Brunner and Noah Linden. “Connection between Bell nonlocality and Bayesian game theory”. Nature Communications 4, 2057 (2013).
https:/​/​doi.org/​10.1038/​ncomms3057

[30] Miguel Navascués, Stefano Pironio, and Antonio Acín. “A convergent hierarchy of semidefinite programs characterizing the set of quantum correlations”. New Journal of Physics 10, 073013 (2008).
https:/​/​doi.org/​10.1088/​1367-2630/​10/​7/​073013

[31] Reinhard F. Werner and Michael M. Wolf. “Bell inequalities and entanglement”. Quantum Information and Computation 1, 1–25 (2001).
https:/​/​doi.org/​10.26421/​QIC1.3-1

[32] Alastair A. Abbott, Mehdi Mhalla, and Pierre Pocreau. code: pierrepocreau/​Improving_QSW.
https:/​/​github.com/​pierrepocreau/​Improving_QSW

Cited by

Could not fetch Crossref cited-by data during last attempt 2024-06-17 14:43:49: Could not fetch cited-by data for 10.22331/q-2024-06-17-1376 from Crossref. This is normal if the DOI was registered recently. On SAO/NASA ADS no data on citing works was found (last attempt 2024-06-17 14:43:50).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

Time Stamp:

More from Quantum Journal