Dipartimento di Fisica e Chimica “Emilio Segrè”, Group of Interdisciplinary Theoretical Physics, Università degli studi di Palermo, Viale delle Scienze, Ed. 18, I-90128 Palermo, Italy
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
Measurement-induced phase transition arises from the competition between a deterministic quantum evolution and a repeated measurement process. We explore the measurement-induced phase transition through the Quantum Fisher Information in two different metrological scenarios. We demonstrate through the scaling behavior of the quantum Fisher information the transition of the multi-partite entanglement across the phases. In analogy with standard quantum phase transition, we reveal signature of a measurement-induced phase transition in the non-analytic behaviour of the quantum Fisher information as the measurement strength approaches the critical value. Our results offer novel insights into the features of a quantum systems undergoing measurement-induced phase transition and indicate potential avenues for further exploration in the field of quantum physics.
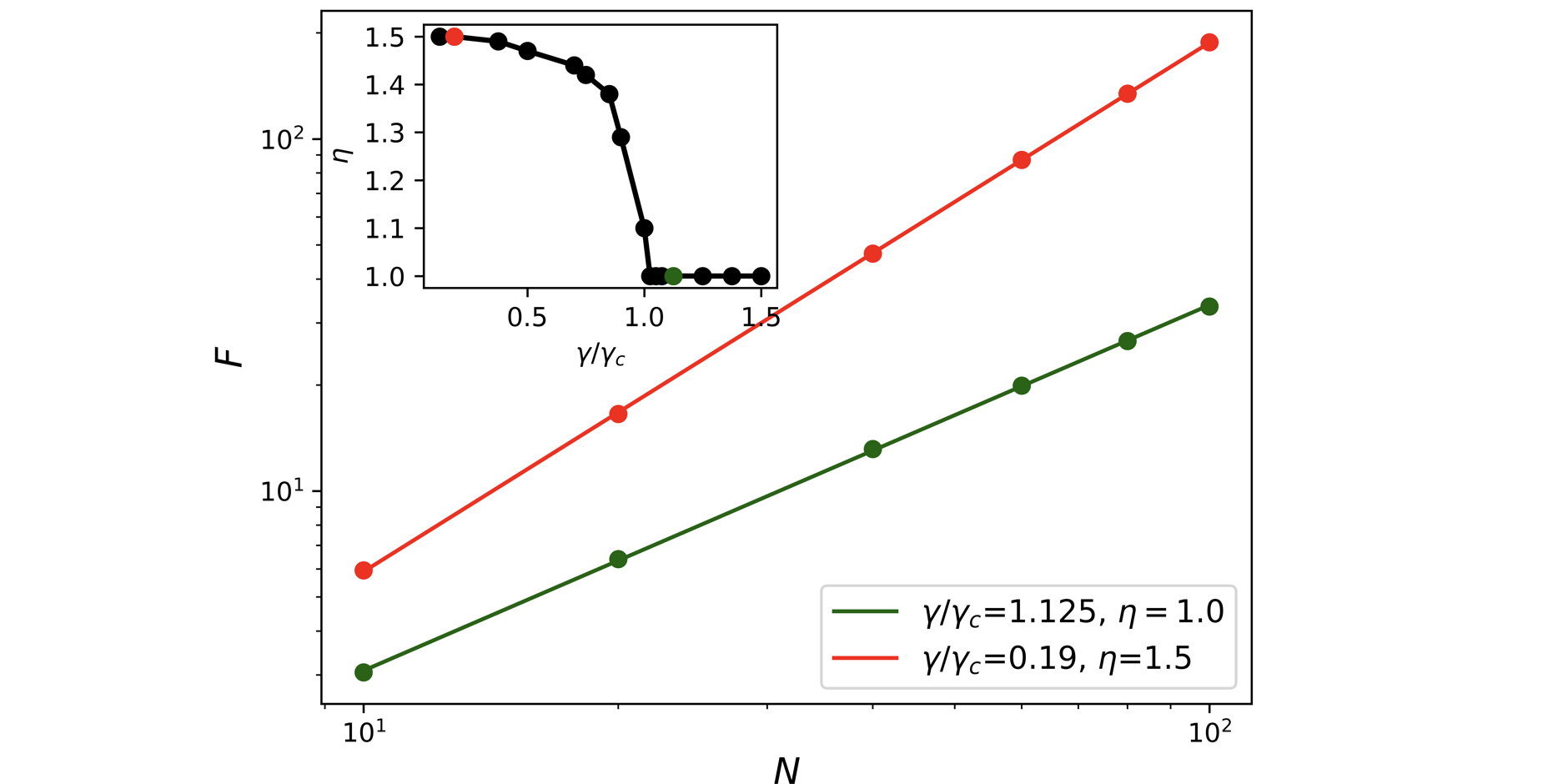
Featured image: Reproduction of the phase diagram through the scaling of the Quantum Fisher information.
Popular summary
► BibTeX data
► References
[1] Davide Rossini and Ettore Vicari. “Measurement-induced dynamics of many-body systems at quantum criticality”. Phys. Rev. B 102, 035119 (2020).
https://doi.org/10.1103/PhysRevB.102.035119
[2] Xiangyu Cao, Antoine Tilloy, and Andrea De Luca. “Entanglement in a fermion chain under continuous monitoring”. SciPost Phys. 7, 024 (2019).
https://doi.org/10.21468/SciPostPhys.7.2.024
[3] O. Alberton, M. Buchhold, and S. Diehl. “Entanglement transition in a monitored free-fermion chain: From extended criticality to area law”. Phys. Rev. Lett. 126, 170602 (2021).
https://doi.org/10.1103/PhysRevLett.126.170602
[4] Alberto Biella and Marco Schiró. “Many-body quantum Zeno effect and measurement-induced subradiance transition”. Quantum 5, 528 (2021).
https://doi.org/10.22331/q-2021-08-19-528
[5] Xhek Turkeshi, Alberto Biella, Rosario Fazio, Marcello Dalmonte, and Marco Schiró. “Measurement-induced entanglement transitions in the quantum Ising chain: From infinite to zero clicks”. Phys. Rev. B 103, 224210 (2021).
https://doi.org/10.1103/PhysRevB.103.224210
[6] Xhek Turkeshi and Marco Schiró. “Entanglement and correlation spreading in non-Hermitian spin chains”. Phys. Rev. B 107, L020403 (2023).
https://doi.org/10.1103/PhysRevB.107.L020403
[7] Takaaki Minato, Koudai Sugimoto, Tomotaka Kuwahara, and Keiji Saito. “Fate of measurement-induced phase transition in long-range interactions”. Phys. Rev. Lett. 128, 010603 (2022).
https://doi.org/10.1103/PhysRevLett.128.010603
[8] Michael J. Gullans and David A. Huse. “Dynamical purification phase transition induced by quantum measurements”. Phys. Rev. X 10, 041020 (2020).
https://doi.org/10.1103/PhysRevX.10.041020
[9] Michael J. Gullans and David A. Huse. “Scalable probes of measurement-induced criticality”. Phys. Rev. Lett. 125, 070606 (2020).
https://doi.org/10.1103/PhysRevLett.125.070606
[10] Amos Chan, Rahul M. Nandkishore, Michael Pretko, and Graeme Smith. “Unitary-projective entanglement dynamics”. Phys. Rev. B 99, 224307 (2019).
https://doi.org/10.1103/PhysRevB.99.224307
[11] Brian Skinner, Jonathan Ruhman, and Adam Nahum. “Measurement-induced phase transitions in the dynamics of entanglement”. Phys. Rev. X 9, 031009 (2019).
https://doi.org/10.1103/PhysRevX.9.031009
[12] Adam Nahum, Sthitadhi Roy, Brian Skinner, and Jonathan Ruhman. “Measurement and entanglement phase transitions in all-to-all quantum circuits, on quantum trees, and in Landau-Ginsburg theory”. PRX Quantum 2, 010352 (2021).
https://doi.org/10.1103/PRXQuantum.2.010352
[13] Soonwon Choi, Yimu Bao, Xiao-Liang Qi, and Ehud Altman. “Quantum error correction in scrambling dynamics and measurement-induced phase transition”. Phys. Rev. Lett. 125, 030505 (2020).
https://doi.org/10.1103/PhysRevLett.125.030505
[14] Shengqi Sang, Yaodong Li, Tianci Zhou, Xiao Chen, Timothy H. Hsieh, and Matthew P.A. Fisher. “Entanglement negativity at measurement-induced criticality”. PRX Quantum 2, 030313 (2021).
https://doi.org/10.1103/PRXQuantum.2.030313
[15] Ali Lavasani, Yahya Alavirad, and Maissam Barkeshli. “Measurement-induced topological entanglement transitions in symmetric random quantum circuits”. Nature Physics 17, 342–347 (2021). arXiv:2004.07243.
https://doi.org/10.1038/s41567-020-01112-z
arXiv:2004.07243
[16] G. Mussardo, Ship Navigation, and Northern Sea Route. “Statistical field theory : an introduction to exactly solved models in statistical physics”. Page 755. Oxford University Press. (2010).
[17] Paolo Zanardi, Matteo G A Paris, and Lorenzo Campos Venuti. “Quantum criticality as a resource for quantum estimation”. Phys. Rev. A 78, 042105 (2008).
https://doi.org/10.1103/PhysRevA.78.042105
[18] Carmen Invernizzi, Michael Korbman, Lorenzo Campos Venuti, and Matteo G. A. Paris. “Optimal quantum estimation in spin systems at criticality”. Phys. Rev. A 78, 042106 (2008).
https://doi.org/10.1103/PhysRevA.78.042106
[19] Mankei Tsang. “Quantum transition-edge detectors”. Phys. Rev. A 88, 021801 (2013).
https://doi.org/10.1103/PhysRevA.88.021801
[20] P. A. Ivanov and D. Porras. “Adiabatic quantum metrology with strongly correlated quantum optical systems”. Phys. Rev. A 88, 023803 (2013).
https://doi.org/10.1103/PhysRevA.88.023803
[21] M Bina, I Amelio, and M. G. A. Paris. “Dicke coupling by feasible local measurements at the superradiant quantum phase transition”. Phys. Rev. E 93, 052118 (2016).
https://doi.org/10.1103/PhysRevE.93.052118
[22] Irénée Frérot and Tommaso Roscilde. “Quantum critical metrology”. Phys. Rev. Lett. 121, 020402 (2018).
https://doi.org/10.1103/PhysRevLett.121.020402
[23] Toni L. Heugel, Matteo Biondi, Oded Zilberberg, and R. Chitra. “Quantum transducer using a parametric driven-dissipative phase transition”. Phys. Rev. Lett. 123, 173601 (2019).
https://doi.org/10.1103/PhysRevLett.123.173601
[24] Louis Garbe, Matteo Bina, Arne Keller, Matteo G. A. Paris, and Simone Felicetti. “Critical quantum metrology with a finite-component quantum phase transition”. Phys. Rev. Lett. 124, 120504 (2020).
https://doi.org/10.1103/PhysRevLett.124.120504
[25] Peter A Ivanov. “Steady-state force sensing with single trapped ion”. Phys. Scr. 95, 025103 (2020).
https://doi.org/10.1088/1402-4896/ab444c
[26] Victor Montenegro, Utkarsh Mishra, and Abolfazl Bayat. “Global sensing and its impact for quantum many-body probes with criticality”. Phys. Rev. Lett. 126, 200501 (2021).
https://doi.org/10.1103/PhysRevLett.126.200501
[27] Francesco Albarelli and Rafał Demkowicz-Dobrzański. “Probe incompatibility in multiparameter noisy quantum metrology”. Phys. Rev. X 12, 011039 (2022).
https://doi.org/10.1103/PhysRevX.12.011039
[28] R. Di Candia, F. Minganti, K. V. Petrovnin, G. S. Paraoanu, and S. Felicetti. “Critical parametric quantum sensing” (2021).
[29] Giovanni Di Fresco, Bernardo Spagnolo, Davide Valenti, and Angelo Carollo. “Multiparameter quantum critical metrology”. SciPost Phys. 13, 077 (2022).
https://doi.org/10.21468/SciPostPhys.13.4.077
[30] Leonardo Banchi, Paolo Giorda, and Paolo Zanardi. “Quantum information-geometry of dissipative quantum phase transitions”. Phys. Rev. E 89, 022102 (2014).
https://doi.org/10.1103/PhysRevE.89.022102
[31] Angelo Carollo, Davide Valenti, and Bernardo Spagnolo. “Geometry of quantum phase transitions”. Phys. Rep. 838, 1–72 (2020).
https://doi.org/10.1016/j.physrep.2019.11.002
[32] Philipp Hyllus, Wiesław Laskowski, Roland Krischek, Christian Schwemmer, Witlef Wieczorek, Harald Weinfurter, Luca Pezzé, and Augusto Smerzi. “Fisher information and multiparticle entanglement”. Phys. Rev. A 85, 022321 (2012).
https://doi.org/10.1103/PhysRevA.85.022321
[33] Géza Tóth. “Multipartite entanglement and high-precision metrology”. Phys. Rev. A 85, 022322 (2012).
https://doi.org/10.1103/PhysRevA.85.022322
[34] Helmut Strobel, Wolfgang Muessel, Daniel Linnemann, Tilman Zibold, David B. Hume, Luca Pezzè, Augusto Smerzi, and Markus K. Oberthaler. “Fisher information and entanglement of non-Gaussian spin states”. Science 345, 424–427 (2014).
https://doi.org/10.1126/science.1250147
[35] Philipp Hauke, Markus Heyl, Luca Tagliacozzo, and Peter Zoller. “Measuring multipartite entanglement through dynamic susceptibilities”. Nature Physics 12, 778–782 (2016).
https://doi.org/10.1038/nphys3700
[36] Carl W. Helstrom. “Quantum detection and estimation theory”. Academic Press. (1976).
[37] Magdalena Szczykulska, Tillmann Baumgratz, and Animesh Datta. “Multi-parameter quantum metrology”. Adv. Phys. X 1, 621–639 (2016).
https://doi.org/10.1080/23746149.2016.1230476
[38] Francesco Albarelli, Marco Barbieri, M.G. Genoni, and Ilaria Gianani. “A perspective on multiparameter quantum metrology: From theoretical tools to applications in quantum imaging”. Phys. Lett. A 384, 126311 (2020).
https://doi.org/10.1016/j.physleta.2020.126311
[39] Manuel A. Ballester. “Entanglement is not very useful for estimating multiple phases”. Phys. Rev. A 70, 032310 (2004).
https://doi.org/10.1103/PhysRevA.70.032310
[40] Cyril Vaneph, Tommaso Tufarelli, and Marco G. Genoni. “Quantum estimation of a two-phase spin rotation”. Quantum Meas. Quantum Metrol. 1, 12–20 (2013).
https://doi.org/10.2478/qmetro-2013-0003
[41] M. G. Genoni, M. G. A. Paris, G. Adesso, H. Nha, P. L. Knight, and M. S. Kim. “Optimal estimation of joint parameters in phase space”. Phys. Rev. A 87, 012107 (2013).
https://doi.org/10.1103/PhysRevA.87.012107
[42] Haidong Yuan and Chi-Hang Fred Fung. “Optimal feedback scheme and universal time scaling for Hamiltonian parameter estimation”. Phys. Rev. Lett. 115, 110401 (2015).
https://doi.org/10.1103/PhysRevLett.115.110401
[43] Dominic W. Berry, Mankei Tsang, Michael J. W. Hall, and Howard M. Wiseman. “Quantum Bell-Ziv-Zakai bounds and Heisenberg limits for waveform estimation”. Phys. Rev. X 5, 031018 (2015).
https://doi.org/10.1103/PhysRevX.5.031018
[44] Manuel Gessner, Luca Pezzè, and Augusto Smerzi. “Sensitivity bounds for multiparameter quantum metrology”. Phys. Rev. Lett. 121, 130503 (2018).
https://doi.org/10.1103/PhysRevLett.121.130503
[45] Jesús Rubio and Jacob Dunningham. “Bayesian multiparameter quantum metrology with limited data”. Phys. Rev. A 101, 032114 (2020).
https://doi.org/10.1103/PhysRevA.101.032114
[46] Angelo Carollo, Bernardo Spagnolo, Alexander A. Dubkov, and Davide Valenti. “On quantumness in multi-parameter quantum estimation”. J. Stat. Mech. Theory Exp. 2019, 094010 (2019).
https://doi.org/10.1088/1742-5468/ab3ccb
[47] Francesco Albarelli, Jamie F. Friel, and Animesh Datta. “Evaluating the Holevo Cramér-Rao bound for multiparameter quantum metrology”. Phys. Rev. Lett. 123, 200503 (2019).
https://doi.org/10.1103/PhysRevLett.123.200503
[48] Jasminder S. Sidhu, Yingkai Ouyang, Earl T. Campbell, and Pieter Kok. “Tight bounds on the simultaneous estimation of incompatible parameters”. Phys. Rev. X 11, 011028 (2021).
https://doi.org/10.1103/PhysRevX.11.011028
[49] Mankei Tsang, Francesco Albarelli, and Animesh Datta. “Quantum semiparametric estimation”. Phys. Rev. X 10, 031023 (2020).
https://doi.org/10.1103/PhysRevX.10.031023
[50] Rafał Demkowicz-Dobrzański, Wojciech Górecki, and Mădălin Guţă. “Multi-parameter estimation beyond quantum Fisher information”. J. Phys. A Math. Theor. 53, 363001 (2020).
https://doi.org/10.1088/1751-8121/ab8ef3
[51] Elliott H. Lieb, Theodore Schultz, and Daniel Mattis. “Two soluble models of an antiferromagnetic chain”. Ann. Phys. (N. Y). 16, 407–466 (1961).
https://doi.org/10.1016/0003-4916(61)90115-4
[52] E Barouch and B M McCoy. “Statistical mechanics of the XY model. II. Spin-correlation functions”. Phys. Rev. A 3, 786–804 (1971).
https://doi.org/10.1103/PhysRevA.3.786
[53] Glen Bigan Mbeng, Angelo Russomanno, and Giuseppe E. Santoro. “The quantum Ising chain for beginners” (2020).
[54] Tony E. Lee and Ching-Kit Chan. “Heralded magnetism in non-Hermitian atomic systems”. Phys. Rev. X 4, 041001 (2014).
https://doi.org/10.1103/PhysRevX.4.041001
[55] Sammy Ragy, Marcin Jarzyna, and Rafał Demkowicz-Dobrzański. “Compatibility in multiparameter quantum metrology”. Phys. Rev. A 94, 052108 (2016).
https://doi.org/10.1103/PhysRevA.94.052108
[56] Jing Liu, Haidong Yuan, Xiao-Ming Lu, and Xiaoguang Wang. “Quantum Fisher information matrix and multiparameter estimation”. Journal of Physics A: Mathematical and Theoretical 53, 023001 (2019).
https://doi.org/10.1088/1751-8121/ab5d4d
[57] Michael Skotiniotis, Pavel Sekatski, and Wolfgang Dür. “Quantum metrology for the Ising Hamiltonian with transverse magnetic field”. New Journal of Physics 17, 073032 (2015).
https://doi.org/10.1088/1367-2630/17/7/073032
[58] Alessio Paviglianiti and Alessandro Silva. “Multipartite entanglement in the measurement-induced phase transition of the quantum ising chain” (2023). arXiv:2302.06477.
arXiv:2302.06477
[59] Ravinder Rupchand Puri. “Algebra of the exponential operator”. Pages 37–53. Springer Berlin Heidelberg. Berlin, Heidelberg (2001).
https://doi.org/10.1007/978-3-540-44953-9_2
Cited by
[1] Sudipto Singha Roy, Soumik Bandyopadhyay, Ricardo Costa de Almeida, and Philipp Hauke, “Unveiling Eigenstate Thermalization for Non-Hermitian systems”, arXiv:2309.00049, (2023).
[2] Sebastien J Avakian, T. Pereg-Barnea, and William Witczak-Krempa, “Long-range multipartite entanglement near measurement-induced transitions”, arXiv:2404.16095, (2024).
The above citations are from SAO/NASA ADS (last updated successfully 2024-04-30 15:44:05). The list may be incomplete as not all publishers provide suitable and complete citation data.
Could not fetch Crossref cited-by data during last attempt 2024-04-30 15:44:04: Could not fetch cited-by data for 10.22331/q-2024-04-30-1326 from Crossref. This is normal if the DOI was registered recently.
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.
- SEO Powered Content & PR Distribution. Get Amplified Today.
- PlatoData.Network Vertical Generative Ai. Empower Yourself. Access Here.
- PlatoAiStream. Web3 Intelligence. Knowledge Amplified. Access Here.
- PlatoESG. Carbon, CleanTech, Energy, Environment, Solar, Waste Management. Access Here.
- PlatoHealth. Biotech and Clinical Trials Intelligence. Access Here.
- Source: https://quantum-journal.org/papers/q-2024-04-30-1326/
- :is
- :not
- ][p
- 001
- 1
- 10
- 11
- 12
- 121
- 125
- 13
- 14
- 15%
- 16
- 17
- 19
- 1961
- 20
- 2001
- 2008
- 2012
- 2013
- 2014
- 2015
- 2016
- 2018
- 2019
- 2020
- 2021
- 2022
- 2023
- 2024
- 22
- 23
- 24
- 25
- 26%
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 35%
- 36
- 39
- 40
- 41
- 43
- 49
- 50
- 51
- 54
- 58
- 7
- 70
- 8
- 87
- 89
- 9
- a
- above
- ABSTRACT
- academic
- access
- across
- Adam
- affiliations
- Alexander
- All
- allows
- an
- and
- ann
- applications
- approaches
- apr
- ARE
- AREA
- arise
- arises
- AS
- At
- atomic
- attempt
- author
- authors
- avenues
- BE
- Beginners
- behavior
- behaviour
- Berlin
- between
- Beyond
- Bound
- bounds
- Break
- Brian
- by
- campbell
- cao
- Carl
- chain
- chains
- chan
- change
- chen
- christian
- comment
- Commons
- competition
- complete
- continuous
- copyright
- Correlation
- costa
- could
- critical
- criticality
- Daniel
- data
- David
- de
- demonstrate
- Detection
- diagram
- different
- discuss
- distinct
- during
- dynamic
- dynamics
- e
- ed
- effect
- Elliott
- enhancement
- entanglement
- error
- evolution
- exactly
- exploration
- explore
- exponential
- extended
- feasible
- Features
- feedback
- field
- For
- Force
- Framework
- from
- functions
- further
- Group
- Hall
- harvard
- here
- High
- Highlight
- holders
- How
- HTTPS
- Hume
- i
- if
- ii
- image
- Imaging
- Impact
- in
- incompatible
- indicate
- Infinite
- information
- insights
- institutions
- interactions
- interesting
- International
- into
- Introduction
- IT
- ITS
- jacob
- Jamie
- JavaScript
- joint
- jonathan
- journal
- Kim
- Knight
- kok
- Last
- Law
- Leave
- Lee
- Li
- License
- Limited
- limits
- List
- local
- Louis
- Magnetic field
- Magnetism
- marcello
- Marco
- math
- mathematical
- Matrix
- matthew
- max-width
- May..
- measurement
- measurements
- mechanics
- Metrology
- Michael
- Mishra
- model
- models
- monitored
- monitoring
- montenegro
- Month
- multiple
- Nature
- Navigation
- Near
- New
- normal
- novel
- of
- offer
- on
- ONE
- open
- operator
- or
- original
- Other
- our
- Oxford
- oxford university
- page
- pages
- Paolo
- Paper
- parameter
- parameters
- paris
- performance
- perspective
- Peter
- phase
- phases
- phenomenon
- Physics
- plato
- Plato Data Intelligence
- PlatoData
- possible
- potential
- press
- process
- processes
- properties
- provide
- provides
- published
- publisher
- publishers
- Qi
- Quantum
- quantum physics
- quantum systems
- R
- random
- recently
- references
- registered
- remains
- repeated
- reproduction
- resource
- Results
- reveal
- Roland
- Route
- roy
- s
- same
- scaling
- scenarios
- scheme
- schemes
- schultz
- Science
- SEA
- SHIP
- show
- signature
- silva
- single
- smith
- Space
- Spin
- Spreading
- standard
- States
- statistical
- strength
- strongly
- Studying
- Successfully
- such
- suitable
- system
- Systems
- The
- their
- theoretical
- theory
- they
- this
- Through
- time
- Title
- to
- Tony
- tools
- transition
- transitions
- trapped
- Trees
- two
- under
- undergoing
- Universal
- university
- unveiling
- updated
- URL
- useful
- using
- utilize
- value
- very
- volume
- W
- wang
- want
- was
- we
- william
- with
- X
- xiao
- year
- Yuan
- zephyrnet
- zero