Partitioning Qubits In Hypergraph Product Codes To Implement Logical Gates

Republished By Plato

Followers: 0

Armanda O. Quintavalle^1,2, Paul Webster³, and Michael Vasmer^4,5

¹Department of Physics & Astronomy, University of Sheffield, Sheffield, S3 7RH, United Kingdom
²Dahlem Center for Complex Quantum Systems, Freie Universität Berlin, 14195 Berlin, Germany
³Centre for Engineered Quantum Systems, School of Physics, The University of Sydney, Sydney, NSW 2006, Australia
⁴Perimeter Institute for Theoretical Physics, Waterloo, ON N2L 2Y5, Canada
⁵Institute for Quantum Computing, University of Waterloo, Waterloo, ON N2L 3G1, Canada

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

The promise of high-rate low-density parity check (LDPC) codes to substantially reduce the overhead of fault-tolerant quantum computation depends on constructing efficient, fault-tolerant implementations of logical gates on such codes. Transversal gates are the simplest type of fault-tolerant gate, but the potential of transversal gates on LDPC codes has hitherto been largely neglected. We investigate the transversal gates that can be implemented in hypergraph product codes, a class of LDPC codes. Our analysis is aided by the construction of a symplectic canonical basis for the logical operators of hypergraph product codes, a result that may be of independent interest. We show that in these codes transversal gates can implement Hadamard (up to logical SWAP gates) and control-Z on all logical qubits. Moreover, we show that sequences of transversal operations, interleaved with error correction, allow implementation of entangling gates between arbitrary pairs of logical qubits in the same code block. We thereby demonstrate that transversal gates can be used as the basis for universal quantum computing on LDPC codes, when supplemented with state injection.

Partitioning qubits in hypergraph product codes to implement logical gates PlatoBlockchain Data Intelligence. Vertical Search. Ai.

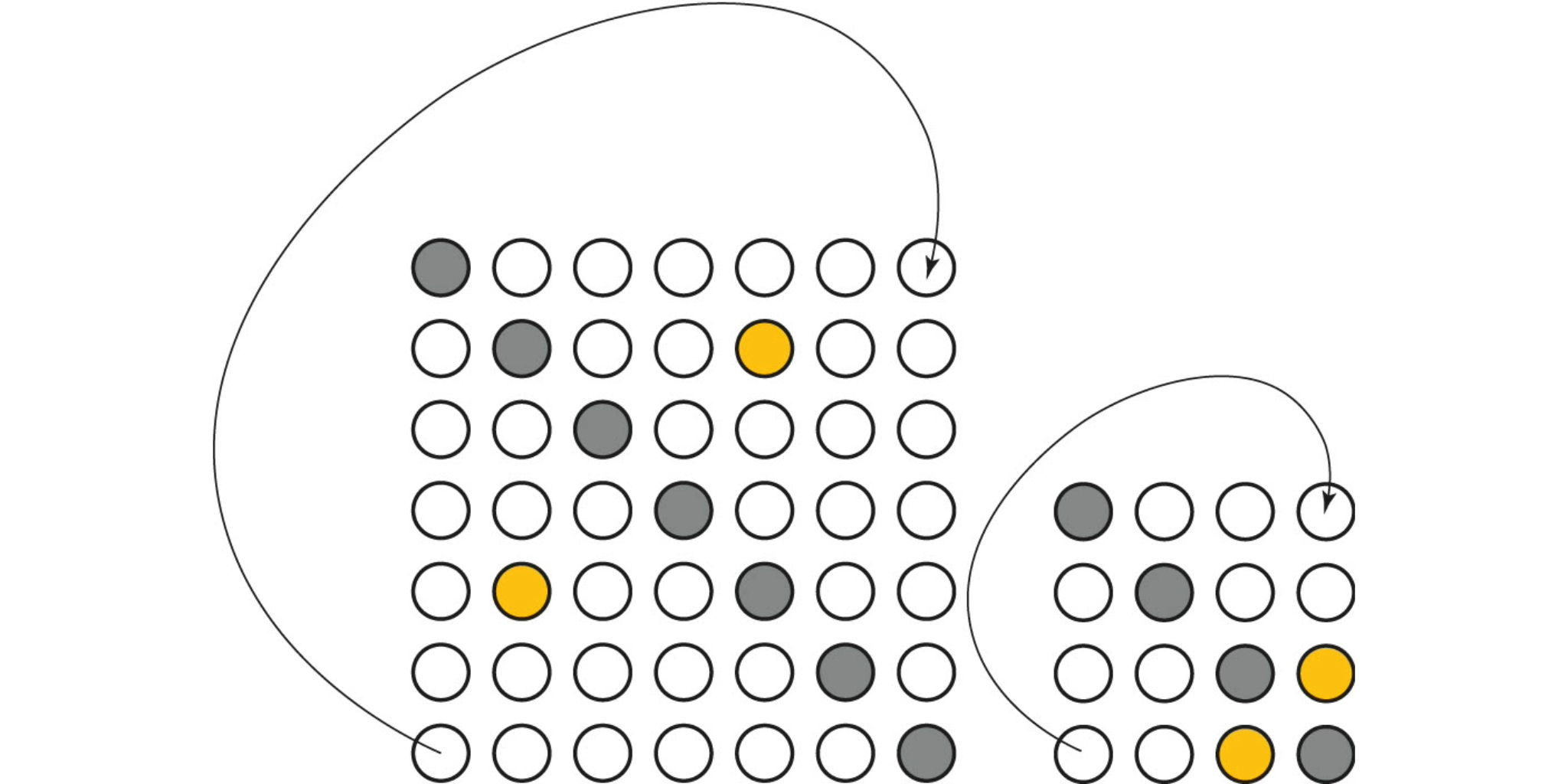
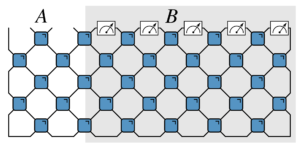
Featured image: Visual representation of the physical qubits within a hypergraph product code, along with its associated symmetries. These symmetries are essential for enabling the implementation of the logical Clifford gates presented in our work.
The physical qubits, depicted as white circles, are organized into two distinct grids: one on the left and another on the right. To achieve the required symmetrical arrangement, each grid is folded along its principal diagonal. Via folding, physical qubits that occupy the same positions on both grids become paired together and are highlighted in yellow. The grey circles on the diagram represent qubits that remain unpaired.

Popular summary

Error correction codes would be of no use without a method for dynamically manipulating the information they store. While the literature offers several techniques for performing gates on codes with just one logical qubit, there are far fewer solutions available for codes that encode multiple logical qubits.
In this paper, we introduce an approach to implement logical encoded gates within hypergraph product codes, even for codes with multiple logical qubits. Our method extends the concept of transversal gates and relies on partitioning the physical qubits within the code in alignment with its logical structure. After demonstrating the fault tolerance of our method, we showcase its application in realizing certain Clifford gates for hypergraph product codes that adhere to specific symmetry constraints.

► BibTeX data

@article{Quintavalle2023partitioningqubits, doi = {10.22331/q-2023-10-24-1153}, url = {https://doi.org/10.22331/q-2023-10-24-1153}, title = {Partitioning qubits in hypergraph product codes to implement logical gates}, author = {Quintavalle, Armanda O. and Webster, Paul and Vasmer, Michael}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {7}, pages = {1153}, month = oct, year = {2023}<br /> }

► References

[1] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Rupak Biswas, Sergio Boixo, Fernando GSL Brandao, David A Buell, et al. “Quantum supremacy using a programmable superconducting processor”. Nature 574, 505–510 (2019).
https://doi.org/10.1038/s41586-019-1666-5

[2] Peter W. Shor. “Fault-tolerant quantum computation”. In Proceedings of 37th Conference on Foundations of Computer Science. Pages 56–65. (1996).
https://doi.org/10.1109/SFCS.1996.548464

[3] Craig Gidney and Martin Ekerå. “How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits”. Quantum 5, 433 (2021).
https://doi.org/10.22331/q-2021-04-15-433

[4] Isaac H Kim, Eunseok Lee, Ye-Hua Liu, Sam Pallister, William Pol, and Sam Roberts. “Fault-tolerant resource estimate for quantum chemical simulations: Case study on Li-ion battery electrolyte molecules”. Physical Review Research 4, 023019 (2022).
https://doi.org/10.1103/PhysRevResearch.4.023019

[5] Nikolas P Breuckmann and Jens Niklas Eberhardt. “Quantum low-density parity-check codes”. PRX Quantum 2, 040101 (2021).
https://doi.org/10.1103/PRXQuantum.2.040101

[6] A Yu Kitaev. “Fault-tolerant quantum computation by anyons”. Annals of Physics 303, 2–30 (2003).
https://doi.org/10.1016/S0003-4916(02)00018-0

[7] Pavel Panteleev and Gleb Kalachev. “Asymptotically good quantum and locally testable classical LDPC codes”. In Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing. Pages 375–388. (2022).
https://doi.org/10.1145/3519935.3520017

[8] Daniel Gottesman. “Fault-tolerant quantum computation with constant overhead”. Quantum Information & Computation 14, 1338–1372 (2014).
https://doi.org/10.26421/QIC14.15-16-5

[9] Anirudh Krishna and David Poulin. “Fault-tolerant gates on hypergraph product codes”. Physical Review X 11, 011023 (2021).
https://doi.org/10.1103/PhysRevX.11.011023

[10] Anirudh Krishna and David Poulin. “Topological wormholes: Nonlocal defects on the toric code”. Physical Review Research 2, 023116 (2020).
https://doi.org/10.1103/PhysRevResearch.2.023116

[11] Lawrence Z Cohen, Isaac H Kim, Stephen D Bartlett, and Benjamin J Brown. “Low-overhead fault-tolerant quantum computing using long-range connectivity”. Science Advances 8, eabn1717 (2022).
https://doi.org/10.1126/sciadv.abn1717

[12] Bei Zeng, Andrew Cross, and Isaac L. Chuang. “Transversality versus universality for additive quantum codes”. IEEE Transactions on Information Theory 57, 6272–6284 (2011).
https://doi.org/10.1109/TIT.2011.2161917

[13] Bryan Eastin and Emanuel Knill. “Restrictions on transversal encoded quantum gate sets”. Physical Review Letters 102, 110502 (2009).
https://doi.org/10.1103/PhysRevLett.102.110502

[14] Sergey Bravyi and Robert König. “Classification of topologically protected gates for local stabilizer codes”. Phys. Rev. Lett. 110, 170503 (2013).
https://doi.org/10.1103/PhysRevLett.110.170503

[15] Fernando Pastawski and Beni Yoshida. “Fault-tolerant logical gates in quantum error-correcting codes”. Phys. Rev. A 91, 012305 (2015).
https://doi.org/10.1103/PhysRevA.91.012305

[16] Tomas Jochym-O’Connor, Aleksander Kubica, and Theodore J Yoder. “Disjointness of stabilizer codes and limitations on fault-tolerant logical gates”. Physical Review X 8, 021047 (2018).
https://doi.org/10.1103/PhysRevX.8.021047

[17] Paul Webster, Michael Vasmer, Thomas R Scruby, and Stephen D Bartlett. “Universal fault-tolerant quantum computing with stabilizer codes”. Physical Review Research 4, 013092 (2022).
https://doi.org/10.1103/PhysRevResearch.4.013092

[18] Sergey Bravyi and Matthew B Hastings. “Homological product codes”. In Proceedings of the 46th Annual ACM Symposium on Theory of Computing. Pages 273–282. ACM (2014).
https://doi.org/10.1145/2591796.2591870

[19] Tomas Jochym-O’Connor. “Fault-tolerant gates via homological product codes”. Quantum 3, 120 (2019).
https://doi.org/10.22331/q-2019-02-04-120

[20] Armanda O Quintavalle, Michael Vasmer, Joschka Roffe, and Earl T Campbell. “Single-shot error correction of three-dimensional homological product codes”. PRX Quantum 2, 020340 (2021).
https://doi.org/10.1103/PRXQuantum.2.020340

[21] Tomas Jochym-O’Connor and Theodore J Yoder. “Four-dimensional toric code with non-Clifford transversal gates”. Physical Review Research 3, 013118 (2021).
https://doi.org/10.1103/PhysRevResearch.3.013118

[22] Shai Evra, Tali Kaufman, and Gilles Zémor. “Decodable quantum LDPC codes beyond the $sqrt{n}$ distance barrier using high-dimensional expanders”. SIAM Journal on ComputingPages FOCS20–276 (2022).
https://doi.org/10.1137/20M1383689

[23] Theodore J Yoder, Ryuji Takagi, and Isaac L Chuang. “Universal fault-tolerant gates on concatenated stabilizer codes”. Physical Review X 6, 031039 (2016).
https://doi.org/10.1103/PhysRevX.6.031039

[24] Alexey A Kovalev and Leonid P Pryadko. “Improved quantum hypergraph-product ldpc codes”. In 2012 IEEE International Symposium on Information Theory Proceedings. Pages 348–352. IEEE (2012).
https://doi.org/10.1109/ISIT.2012.6284206

[25] David JC MacKay. “Information theory, inference and learning algorithms”. Cambridge University Press. (2003).

[26] A Robert Calderbank and Peter W Shor. “Good quantum error-correcting codes exist”. Physical Review A 54, 1098 (1996).
https://doi.org/10.1103/PhysRevA.54.1098

[27] Andrew Steane. “Multiple-particle interference and quantum error correction”. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 452, 2551–2577 (1996).
https://doi.org/10.1098/rspa.1996.0136

[28] Michael A Nielsen and Isaac Chuang. “Quantum computation and quantum information”. Cambridge University Press. (2002).

[29] Jean-Pierre Tillich and Gilles Zémor. “Quantum LDPC codes with positive rate and minimum distance proportional to the square root of the blocklength”. IEEE Transactions on Information Theory 60, 1193–1202 (2014).
https://doi.org/10.1109/TIT.2013.2292061

[30] Benjamin Audoux and Alain Couvreur. “On tensor products of CSS codes” (2015). arXiv:1512.07081.
arXiv:1512.07081

[31] Armanda O Quintavalle and Earl T Campbell. “Reshape: A decoder for hypergraph product codes”. IEEE Transactions on Information Theory 68, 6569–6584 (2022).
https://doi.org/10.1109/TIT.2022.3184108

[32] Alexey A Kovalev and Leonid P Pryadko. “Quantum kronecker sum-product low-density parity-check codes with finite rate”. Physical Review A 88, 012311 (2013).
https://doi.org/10.1103/PhysRevA.88.012311

[33] Simon Burton and Dan Browne. “Limitations on transversal gates for hypergraph product codes”. IEEE Transactions on Information Theory 68, 1772–1781 (2022).
https://doi.org/10.1109/TIT.2021.3131043

[34] Aleksander Kubica, Beni Yoshida, and Fernando Pastawski. “Unfolding the color code”. New Journal of Physics 17, 083026 (2015).
https://doi.org/10.1088/1367-2630/17/8/083026

[35] Jonathan E Moussa. “Transversal Clifford gates on folded surface codes”. Physical Review A 94, 042316 (2016).
https://doi.org/10.1103/PhysRevA.94.042316

[36] Michael Vasmer and Dan E Browne. “Three-dimensional surface codes: Transversal gates and fault-tolerant architectures”. Physical Review A 100, 012312 (2019).
https://doi.org/10.1103/PhysRevA.100.012312

[37] Nikolas P Breuckmann and Simon Burton. “Fold-transversal Clifford gates for quantum codes” (2022). arXiv:2202.06647.
arXiv:2202.06647

[38] Raymond Laflamme, Cesar Miquel, Juan Pablo Paz, and Wojciech Hubert Zurek. “Perfect quantum error correcting code”. Physical Review Letters 77, 198 (1996).
https://doi.org/10.1103/PhysRevLett.77.198

[39] Rui Chao and Ben W Reichardt. “Fault-tolerant quantum computation with few qubits”. npj Quantum Information 4, 1–8 (2018).
https://doi.org/10.1038/s41534-018-0085-z

[40] Daniel Gottesman and Isaac L. Chuang. “Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations”. Nature 402, 390–393 (1999).
https://doi.org/10.1038/46503

[41] Xinlan Zhou, Debbie W. Leung, and Isaac L. Chuang. “Methodology for quantum logic gate construction”. Physical Review A 62, 052316 (2000).
https://doi.org/10.1103/PhysRevA.62.052316

[42] Sergey Bravyi and Alexei Kitaev. “Universal quantum computation with ideal Clifford gates and noisy ancillas”. Physical Review A 71, 022316 (2005).
https://doi.org/10.1103/PhysRevA.71.022316

[43] Emanuel Knill, Raymond Laflamme, and Wojciech Zurek. “Resilient quantum computation”. Science 279, 342–345 (1996).
https://doi.org/10.1126/science.279.5349.342

[44] A.M. Steane. “Quantum Reed-Muller codes”. IEEE Transactions on Information Theory 45, 1701–1703 (1999).
https://doi.org/10.1109/18.771249

[45] Jonas T. Anderson, Guillaume Duclos-Cianci, and David Poulin. “Fault-tolerant conversion between the Steane and Reed-Muller quantum codes”. Physical Review Letters 113, 080501 (2014).
https://doi.org/10.1103/PhysRevLett.113.080501

[46] Sergey Bravyi and Jeongwan Haah. “Magic-state distillation with low overhead”. Physical Review A 86, 052329 (2012).
https://doi.org/10.1103/PhysRevA.86.052329

[47] Daniel Litinski. “Magic state distillation: Not as costly as you think”. Quantum 3, 205 (2019).
https://doi.org/10.22331/q-2019-12-02-205

[48] Christopher Chamberland and Kyungjoo Noh. “Very low overhead fault-tolerant magic state preparation using redundant ancilla encoding and flag qubits”. npj Quantum Information 6, 1–12 (2020).
https://doi.org/10.1038/s41534-020-00319-5

[49] Matthew B Hastings. “Weight reduction for quantum codes”. Quantum Information & Computation 17, 1307–1334 (2016).
https://doi.org/10.26421/QIC17.15-16-4

[50] MB Hastings. “On quantum weight reduction” (2021). arXiv:2102.10030.
arXiv:2102.10030

[51] Pavel Panteleev and Gleb Kalachev. “Degenerate quantum LDPC codes with good finite length performance”. Quantum 5, 585 (2021).
https://doi.org/10.22331/q-2021-11-22-585

[52] Matthew B Hastings, Jeongwan Haah, and Ryan O’Donnell. “Fiber bundle codes: breaking the $N^{1/2}text{polylog}(N)$ barrier for quantum LDPC codes”. In Proceedings of the 53rd Annual ACM SIGACT Symposium on Theory of Computing. Pages 1276–1288. (2021).
https://doi.org/10.1145/3406325.3451005

[53] Nikolas P Breuckmann and Jens N Eberhardt. “Balanced product quantum codes”. IEEE Transactions on Information Theory 67, 6653–6674 (2021).
https://doi.org/10.1109/TIT.2021.3097347

[54] Anthony Leverrier and Gilles Zémor. “Quantum tanner codes”. In 2022 IEEE 63rd Annual Symposium on Foundations of Computer Science (FOCS). Pages 872–883. IEEE (2022).
https://doi.org/10.1109/FOCS54457.2022.00117

[55] Wieb Bosma, John Cannon, and Catherine Playoust. “The Magma algebra system I: The user language”. Journal of Symbolic Computation 24, 235–265 (1997).
https://doi.org/10.1006/jsco.1996.0125

[56] Markus Grassl. “Bounds on the minimum distance of linear codes” (2008). http://www.codetables.de.
http://www.codetables.de

Cited by

[1] Oscar Higgott and Nikolas P. Breuckmann, “Constructions and performance of hyperbolic and semi-hyperbolic Floquet codes”, arXiv:2308.03750, (2023).

[2] Qian Xu, J. Pablo Bonilla Ataides, Christopher A. Pattison, Nithin Raveendran, Dolev Bluvstein, Jonathan Wurtz, Bane Vasic, Mikhail D. Lukin, Liang Jiang, and Hengyun Zhou, “Constant-Overhead Fault-Tolerant Quantum Computation with Reconfigurable Atom Arrays”, arXiv:2308.08648, (2023).

[3] Daniel Gottesman, “Opportunities and Challenges in Fault-Tolerant Quantum Computation”, arXiv:2210.15844, (2022).

[4] Yifan Hong, Matteo Marinelli, Adam M. Kaufman, and Andrew Lucas, “Long-range-enhanced surface codes”, arXiv:2309.11719, (2023).

[5] Shilin Huang, Tomas Jochym-O’Connor, and Theodore J. Yoder, “Homomorphic Logical Measurements”, PRX Quantum 4 3, 030301 (2023).

[6] Alexander Cowtan, “Towards surgery with good quantum LDPC codes”, arXiv:2309.16406, (2023).

[7] Mark A. Webster, Armanda O. Quintavalle, and Stephen D. Bartlett, “Transversal diagonal logical operators for stabiliser codes”, New Journal of Physics 25 10, 103018 (2023).

[8] Argyris Giannisis Manes and Jahan Claes, “Distance-preserving stabilizer measurements in hypergraph product codes”, arXiv:2308.15520, (2023).

[9] Alexander Cowtan and Simon Burton, “CSS code surgery as a universal construction”, arXiv:2301.13738, (2023).

[10] Christophe Vuillot, Alessandro Ciani, and Barbara M. Terhal, “Homological Quantum Rotor Codes: Logical Qubits from Torsion”, arXiv:2303.13723, (2023).

The above citations are from SAO/NASA ADS (last updated successfully 2023-10-24 16:24:57). The list may be incomplete as not all publishers provide suitable and complete citation data.

Could not fetch Crossref cited-by data during last attempt 2023-10-24 16:24:55: Could not fetch cited-by data for 10.22331/q-2023-10-24-1153 from Crossref. This is normal if the DOI was registered recently.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

SEO Powered Content & PR Distribution. Get Amplified Today.
PlatoData.Network Vertical Generative Ai. Empower Yourself. Access Here.
PlatoAiStream. Web3 Intelligence. Knowledge Amplified. Access Here.
PlatoESG. Carbon, CleanTech, Energy, Environment, Solar, Waste Management. Access Here.
PlatoHealth. Biotech and Clinical Trials Intelligence. Access Here.
Source: https://quantum-journal.org/papers/q-2023-10-24-1153/

Time Stamp: October 24, 2023

Time Stamp: Jul 26, 2023

Partitioning qubits in hypergraph product codes to implement logical gates

Republished By Plato

Abstract

Popular summary

► BibTeX data

► References

Cited by

More from Quantum Journal

Continuous-time quantum walks for MAX-CUT are hot

Parity Quantum Optimization: Benchmarks

Emergent quantum state designs and biunitarity in dual-unitary circuit dynamics

Enabling Multi-programming Mechanism for Quantum Computing in the NISQ Era

The minimal communication cost for simulating entangled qubits

Abstraqt: Analysis of Quantum Circuits via Abstract Stabilizer Simulation

Determining the ability for universal quantum computing: Testing controllability via dimensional expressivity

Entanglement catalysis for quantum states and noisy channels

Testing symmetry on quantum computers

Three numerical approaches to find mutually unbiased bases using Bell inequalities

Circuits of space and time quantum channels

About Us

Vertical Search & Ai

Platform

Stay Connected

Account