Guia definitivo para clustering K-Means com Scikit-Learn

Introdução

Agrupamento K-Means é um dos algoritmos de aprendizado de máquina não supervisionados mais usados ​​que formam clusters de dados com base na semelhança entre instâncias de dados.

Neste guia, veremos primeiro um exemplo simples para entender como o algoritmo K-Means funciona antes de implementá-lo usando o Scikit-Learn. Em seguida, discutiremos como determinar o número de clusters (Ks) no K-Means e também abordaremos as métricas de distância, variância e prós e contras do K-Means.

Motivação

Imagine a seguinte situação. Um dia, ao passear pelo bairro, você notou que havia 10 lojas de conveniência e começou a se perguntar quais lojas eram semelhantes – mais próximas umas das outras na proximidade. Ao pesquisar maneiras de responder a essa pergunta, você se deparou com uma abordagem interessante que divide as lojas em grupos com base em suas coordenadas em um mapa.

Por exemplo, se uma loja estivesse localizada 5 km a oeste e 3 km ao norte - você atribuiria (5, 3) coordenadas para ele, e representá-lo em um gráfico. Vamos traçar este primeiro ponto para visualizar o que está acontecendo:

import matplotlib.pyplot as plt

plt.title("Store With Coordinates (5, 3)")
plt.scatter(x=5, y=3)

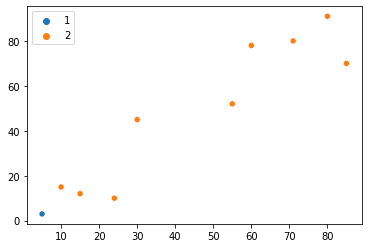
Este é apenas o primeiro ponto, para que possamos ter uma ideia de como podemos representar uma loja. Digamos que já temos 10 coordenadas para as 10 lojas coletadas. Depois de organizá-los em numpy array, também podemos traçar suas localizações:

import numpy as np

points = np.array([[5, 3], [10, 15], [15, 12], [24, 10], [30, 45], [85, 70], [71, 80], [60, 78], [55, 52],[80, 91]])

xs = points[:,0] 
ys = points[:,1]  

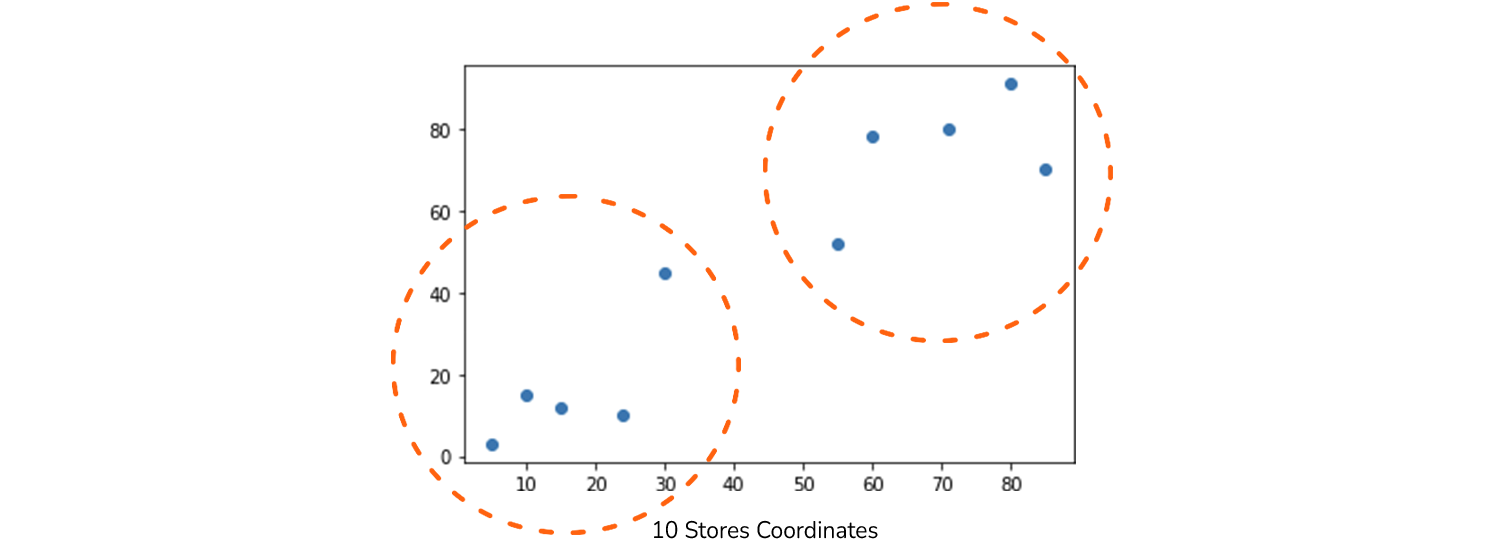
plt.title("10 Stores Coordinates")
plt.scatter(x=xs, y=ys)

Como implementar manualmente o algoritmo K-Means

Agora podemos olhar para as 10 lojas em um gráfico, e o principal problema é encontrar uma maneira de dividi-las em diferentes grupos com base na proximidade? Dando uma olhada rápida no gráfico, provavelmente perceberemos dois grupos de lojas – um são os pontos inferiores no canto inferior esquerdo e o outro são os pontos superiores direito. Talvez possamos até diferenciar esses dois pontos no meio como um grupo separado – criando assim três grupos diferentes.

Nesta seção, veremos o processo de agrupamento manual de pontos – dividindo-os em um determinado número de grupos. Dessa forma, vamos essencialmente passar por cima de todas as etapas do Algoritmo de agrupamento K-Means. Ao final desta seção, você obterá uma compreensão intuitiva e prática de todas as etapas realizadas durante o agrupamento K-Means. Depois disso, vamos delegá-lo ao Scikit-Learn.

Qual seria a melhor maneira de determinar se existem dois ou três grupos de pontos? Uma maneira simples seria simplesmente escolher um número de grupos – por exemplo, dois – e então tentar agrupar pontos com base nessa escolha.

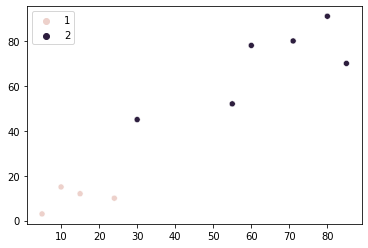
Digamos que decidimos que existem dois grupos das nossas lojas (pontos). Agora, precisamos encontrar uma maneira de entender quais pontos pertencem a qual grupo. Isso pode ser feito escolhendo um ponto para representar grupo 1 e um para representar grupo 2. Esses pontos serão usados ​​como referência ao medir a distância de todos os outros pontos para cada grupo.

Dessa forma, diga ponto (5, 3) acaba pertencendo ao grupo 1, e ponto (79, 60) ao grupo 2. Ao tentar atribuir um novo ponto (6, 3) para grupos, precisamos medir sua distância a esses dois pontos. No caso do ponto (6, 3) is mais próximo ao (5, 3), portanto pertence ao grupo representado por aquele ponto – grupo 1. Desta forma, podemos agrupar facilmente todos os pontos em grupos correspondentes.

Neste exemplo, além de determinar o número de grupos (cachos) – também estamos escolhendo alguns pontos para referência de distância para novos pontos de cada grupo.

Essa é a ideia geral para entender as semelhanças entre nossas lojas. Vamos colocá-lo em prática - podemos primeiro escolher os dois pontos de referência em acaso. O ponto de referência de grupo 1 será (5, 3) e o ponto de referência grupo 2 será (10, 15). Podemos selecionar ambos os pontos de nossa numpy matriz por [0] e [1] índices e armazená-los em g1 (grupo 1) e g2 (grupo 2) variáveis:

g1 = points[0]
g2 = points[1]

Depois de fazer isso, precisamos calcular a distância de todos os outros pontos para esses pontos de referência. Isso levanta uma questão importante – como medir essa distância. Podemos essencialmente usar qualquer medida de distância, mas, para os propósitos deste guia, vamos usar a Distância Euclidiana_.

Pode ser útil saber que a medida de distância euclidiana é baseada no teorema de Pitágoras:

$$
c^2 = a^2 + b^2
$$

Quando adaptado a pontos em um plano – (a1, b1) e (a2, b2), a fórmula anterior se torna:

$$
c^2 = (a2-a1)^2 + (b2-b1)^2
$$

A distância será a raiz quadrada de c, então também podemos escrever a fórmula como:

$$
euclidiano_{dist} = sqrt[2][(a2 – a1)^2 + (b2 – b1) ^2)]
$$

Até agora, escolhemos os pontos para representar grupos e sabemos calcular distâncias. Agora, vamos juntar as distâncias e os grupos atribuindo cada um de nossos pontos de armazenamento coletados a um grupo.

Para melhor visualizar isso, vamos declarar três listas. O primeiro a armazenar pontos do primeiro grupo – points_in_g1. O segundo para armazenar pontos do grupo 2 – points_in_g2, e o último - groupà rótulo os pontos tanto 1 (pertence ao grupo 1) ou 2 (pertence ao grupo 2):

points_in_g1 = []
points_in_g2 = []
group = []

Agora podemos percorrer nossos pontos e calcular a distância euclidiana entre eles e cada uma de nossas referências de grupo. Cada ponto será mais próximo a um dos dois grupos - com base em qual grupo está mais próximo, atribuiremos cada ponto à lista correspondente, além de adicionar 1 or 2 ao group Lista:

for p in points:
    x1, y1 = p[0], p[1]
    euclidean_distance_g1 = np.sqrt((g1[0] - x1)**2 + (g1[1] - y1)**2)
    euclidean_distance_g2 = np.sqrt((g2[0] - x1)**2 + (g2[1] - y1)**2)
    if euclidean_distance_g1 < euclidean_distance_g2:
        points_in_g1.append(p)
        group.append('1')
    else:
        points_in_g2.append(p)
        group.append('2')

Vejamos os resultados desta iteração para ver o que aconteceu:

print(f'points_in_g1:{points_in_g1}n 
npoints_in_g2:{points_in_g2}n 
ngroup:{group}')

O que resulta em:

points_in_g1:[array([5, 3])]
 
points_in_g2:[array([10, 15]), array([15, 12]), 
              array([24, 10]), array([30, 45]), 
              array([85, 70]), array([71, 80]),
              array([60, 78]), array([55, 52]), 
              array([80, 91])]
 
group:[1, 2, 2, 2, 2, 2, 2, 2, 2, 2] 

Também podemos plotar o resultado do agrupamento, com cores diferentes com base nos grupos atribuídos, usando o Seaborn's scatterplot() com o group como um hue argumento:

import seaborn as sns

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

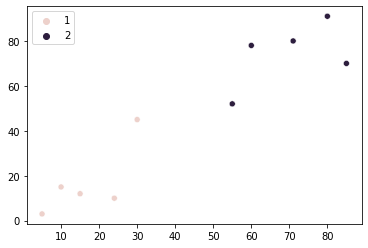
É claramente visível que apenas nosso primeiro ponto é atribuído ao grupo 1, e todos os outros pontos foram atribuídos ao grupo 2. Esse resultado difere do que imaginávamos no início. Considerando a diferença entre nossos resultados e nossas expectativas iniciais – existe uma maneira de mudar isso? Parece que existe!

Uma abordagem é repetir o processo e escolher diferentes pontos para serem as referências dos grupos. Isso mudará nossos resultados, esperamos, mais de acordo com o que imaginamos no início. Desta segunda vez, poderíamos escolhê-los não aleatoriamente como fizemos anteriormente, mas obtendo um significar de todos os nossos pontos já agrupados. Dessa forma, esses novos pontos poderiam ser posicionados no meio dos grupos correspondentes.

Por exemplo, se o segundo grupo tivesse apenas pontos (10, 15), (30, 45). O novo central ponto seria (10 + 30)/2 e (15+45)/2 – que é igual a (20, 30).

Como colocamos nossos resultados em listas, podemos convertê-los primeiro em numpy matrizes, selecione seus xs, ys e, em seguida, obtenha o significar:

g1_center = [np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()]
g2_center = [np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()]
g1_center, g2_center

Para ajudar a repetir o processo com nossos novos pontos centrais, vamos transformar nosso código anterior em uma função, executá-lo e ver se houve alguma alteração na forma como os pontos são agrupados:

def assigns_points_to_two_groups(g1_center, g2_center):
    points_in_g1 = []
    points_in_g2 = []
    group = []

    for p in points:
        x1, y1 = p[0], p[1]
        euclidean_distance_g1 = np.sqrt((g1_center[0] - x1)**2 + (g1_center[1] - y1)**2)
        euclidean_distance_g2 = np.sqrt((g2_center[0] - x1)**2 + (g2_center[1] - y1)**2)
        if euclidean_distance_g1 < euclidean_distance_g2:
            points_in_g1.append(p)
            group.append(1)
        else:
            points_in_g2.append(p)
            group.append(2)
    return points_in_g1, points_in_g2, group

Vamos chamar a função e armazenar seus resultados em points_in_g1, points_in_g2 e group variáveis:

points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
points_in_g1, points_in_g2, group

E também trace o gráfico de dispersão com os pontos coloridos para visualizar a divisão dos grupos:

sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

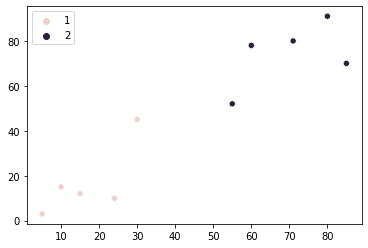
Parece que o agrupamento de nossos pontos é ficando melhor. Mas ainda assim, existem dois pontos no meio do gráfico que podem ser atribuídos a qualquer grupo ao considerar sua proximidade com ambos os grupos. O algoritmo que desenvolvemos até agora atribui esses dois pontos ao segundo grupo.

Isso significa que provavelmente podemos repetir o processo mais uma vez tomando a média dos Xs e Ys, criando dois novos pontos centrais (centroides) aos nossos grupos e reatribuindo-os com base na distância.

Vamos também criar uma função para atualizar os centroides. Todo o processo agora pode ser reduzido a várias chamadas dessa função:

def updates_centroids(points_in_g1, points_in_g2):
    g1_center = np.array(points_in_g1)[:, 0].mean(), np.array(points_in_g1)[:, 1].mean()
    g2_center = np.array(points_in_g2)[:, 0].mean(), np.array(points_in_g2)[:, 1].mean()
    return g1_center, g2_center

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

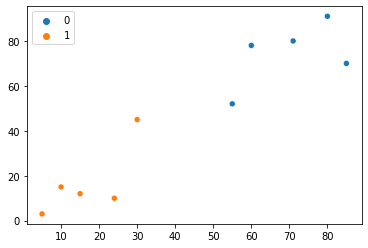
Observe que após esta terceira iteração, cada um dos pontos agora pertence a diferentes clusters. Parece que os resultados estão melhorando – vamos fazer isso mais uma vez. Agora indo para o quarta iteração do nosso método:

g1_center, g2_center = updates_centroids(points_in_g1, points_in_g2)
points_in_g1, points_in_g2, group = assigns_points_to_two_groups(g1_center, g2_center)
sns.scatterplot(x=points[:, 0], y=points[:, 1], hue=group)

Esta quarta vez que temos o mesmo resultado como o anterior. Então parece que nossos pontos não vão mais mudar de grupo, nosso resultado alcançou algum tipo de estabilidade – chegou a um estado imutável, ou convergido. Além disso, temos exatamente o mesmo resultado que imaginávamos para os 2 grupos. Também podemos ver se essa divisão alcançada faz sentido.

Vamos recapitular rapidamente o que fizemos até agora. Dividimos nossas 10 lojas geograficamente em duas seções – uma na região sudoeste e outra no nordeste. Pode ser interessante coletar mais dados além do que já temos – receita, número diário de clientes e muito mais. Dessa forma podemos realizar uma análise mais rica e possivelmente gerar resultados mais interessantes.

Estudos de agrupamento como esse podem ser realizados quando uma marca já estabelecida deseja escolher uma área para abrir uma nova loja. Nesse caso, há muito mais variáveis ​​levadas em consideração além da localização.

O que tudo isso tem a ver com o algoritmo K-Means?

Ao seguir essas etapas, você deve ter se perguntado o que elas têm a ver com o algoritmo K-Means. O processo que conduzimos até agora é o Algoritmo K-Means. Resumindo, determinamos o número de grupos/clusters, escolhemos aleatoriamente os pontos iniciais e atualizamos os centroides em cada iteração até que os clusters convergissem. Basicamente, executamos todo o algoritmo manualmente – conduzindo cuidadosamente cada etapa.

A K em K-Means vem do número de clusters que precisam ser definidos antes de iniciar o processo de iteração. No nosso caso K = 2. Essa característica às vezes é vista como negativo considerando que existem outros métodos de clustering, como Hierarchical Clustering, que não precisam ter um número fixo de clusters previamente.

Devido ao uso de meios, K-means também se torna sensível a outliers e valores extremos – eles aumentam a variabilidade e tornam mais difícil para nossos centróides desempenharem seu papel. Portanto, esteja consciente da necessidade de realizar valores extremos e análise de outliers antes de realizar um agrupamento usando o algoritmo K-Means.

Além disso, observe que nossos pontos foram segmentados em partes retas, não há curvas ao criar os clusters. Isso também pode ser uma desvantagem do algoritmo K-Means.

K-Means também tem muitos vantagens! Ele funciona bem em grandes conjuntos de dados que pode se tornar difícil de manusear se você estiver usando alguns tipos de algoritmos de agrupamento hierárquico. Isso também garante a convergência, e pode facilmente generalizar e adaptar. Além disso, é provavelmente o algoritmo de agrupamento mais utilizado.

Agora que passamos por todas as etapas realizadas no algoritmo K-Means e entendemos todos os seus prós e contras, podemos finalmente implementar o K-Means usando a biblioteca Scikit-Learn.

Como implementar o algoritmo K-Means usando scikit-learn

Para verificar nosso resultado, vamos fazer esse processo novamente, mas agora usando 3 linhas de código com sklearn:

from sklearn.cluster import KMeans


kmeans = KMeans(n_clusters=2, random_state=42) 
kmeans.fit(points)
kmeans.labels_

Aqui, os rótulos são os mesmos dos nossos grupos anteriores. Vamos plotar rapidamente o resultado:

sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

O gráfico resultante é o mesmo da seção anterior.

Com o Scikit-Learn, você também pode inicializar o K-Means para uma convergência mais rápida, definindo o init='k-means++' argumento. Em termos mais amplos, K-Means++ ainda escolhe o k centros de cluster iniciais aleatoriamente seguindo uma distribuição uniforme. Então, cada centro de cluster subsequente é escolhido a partir dos pontos de dados restantes, não calculando apenas uma medida de distância – mas usando probabilidade. Usar a probabilidade acelera o algoritmo e é útil ao lidar com conjuntos de dados muito grandes.

O Método do Cotovelo – Escolhendo o Melhor Número de Grupos

Até agora tudo bem! Agrupamos 10 lojas com base na distância euclidiana entre pontos e centroides. Mas e aqueles dois pontos no meio do gráfico que são um pouco mais difíceis de agrupar? Eles não poderiam formar um grupo separado também? Será que cometemos um erro ao escolher K = 2 grupos? Talvez nós realmente tivéssemos K = 3 grupos? Poderíamos até ter mais de três grupos e não estarmos cientes disso.

A pergunta que está sendo feita aqui é como determinar o número de grupos (K) em K-Means. Para responder a essa pergunta, precisamos entender se haveria um cluster “melhor” para um valor diferente de K.

A maneira ingênua de descobrir isso é agrupando pontos com diferentes valores de K, assim, para K=2, K=3, K=4 e assim por diante:

for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 

Mas, agrupando pontos para diferentes Ks sozinho não será suficiente para entender se escolhemos o valor ideal para K. Precisamos de uma maneira de avaliar a qualidade do agrupamento para cada K nós escolhemos.

Calculando manualmente o Dentro da soma dos quadrados do cluster (WCSS)

Aqui é o lugar ideal para introduzir uma medida de quanto nossos pontos agrupados estão próximos uns dos outros. Basicamente descreve o quanto variação temos dentro de um único cluster. Essa medida é chamada Dentro do Cluster Soma de Quadradosou WCSS como diminutivo. Quanto menor for o WCSS, mais próximos estarão nossos pontos, portanto teremos um cluster mais bem formado. A fórmula WCSS pode ser usada para qualquer número de clusters:

$$
WCSS = soma(Pi_1 – Centroid_1)^2 + cdots + soma(Pi_n – Centroid_n)^2
$$

Agora podemos assumir que optamos por ter dois clusters e tentar implementar o WCSS para entender melhor o que é o WCSS e como usá-lo. Como a fórmula indica, precisamos somar as diferenças quadradas entre todos os pontos do cluster e os centróides. Então, se nosso primeiro ponto do primeiro grupo é (5, 3) e nosso último centróide (após a convergência) do primeiro grupo é (16.8, 17.0), o WCSS será:

$$
WCSS = soma((5,3) – (16.8, 17.0))^2
$$

$$
WCSS = soma((5-16.8) + (3-17.0))^2
$$

$$
WCSS = soma((-11.8) + (-14.0))^2
$$

$$
WCSS = soma((-25.8))^2
$$

$$
WCSS = 335.24
$$

Este exemplo ilustra como calculamos o WCSS para um ponto do cluster. Mas o cluster geralmente contém mais de um ponto, e precisamos levar todos eles em consideração ao calcular o WCSS. Faremos isso definindo uma função que recebe um cluster de pontos e centróides e retorna a soma dos quadrados:

def sum_of_squares(cluster, centroid):
    squares = []
    for p in cluster:
        squares.append((p - centroid)**2)
        ss = np.array(squares).sum()
    return ss

Agora podemos obter a soma dos quadrados para cada cluster:

g1 = sum_of_squares(points_in_g1, g1_center)
g2 = sum_of_squares(points_in_g2, g2_center)

E some os resultados para obter o total WCSS:

g1 + g2

Isto resulta em:

2964.3999999999996

Então, no nosso caso, quando K é igual a 2, o WCSS total é 2964.39. Agora, podemos alternar Ks e calcular o WCSS para todos eles. Dessa forma, podemos ter uma ideia do que K devemos escolher fazer com que nosso cluster tenha o melhor desempenho.

Calculando WCSS utilização scikit-learn

Felizmente, não precisamos calcular manualmente o WCSS para cada K. Depois de realizar o agrupamento K-Means para um determinado número de clusters, podemos obter seu WCSS usando o inertia_ atributo. Agora, podemos voltar ao nosso K-Means for loop, use-o para alternar o número de clusters e liste os valores WCSS correspondentes:

wcss = [] 
for number_of_clusters in range(1, 11): 
    kmeans = KMeans(n_clusters = number_of_clusters, random_state = 42)
    kmeans.fit(points) 
    wcss.append(kmeans.inertia_)
wcss

Observe que o segundo valor na lista é exatamente o mesmo que calculamos antes para K = 2:

[18272.9, # For k=1 
 2964.3999999999996, # For k=2
 1198.75, # For k=3
 861.75,
 570.5,
 337.5,
 175.83333333333334,
 79.5,
 17.0,
 0.0]

Para visualizar esses resultados, vamos plotar nossa Ks juntamente com os valores WCSS:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
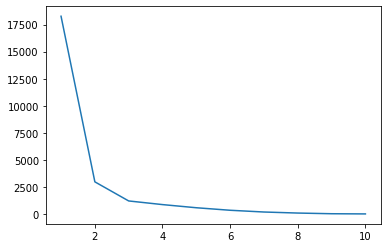
plt.plot(ks, wcss)

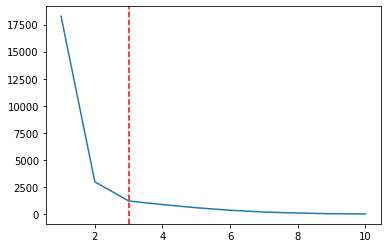
Há uma interrupção em uma trama quando x = 2, um ponto baixo na linha, e um ainda mais baixo quando x = 3. Perceba que isso nos lembra do forma de cotovelo. Ao plotar os Ks junto com o WCSS, estamos usando o Método do cotovelo para escolher o número de Ks. E a K escolhido é exatamente o ponto mais baixo do cotovelo, então seria 3 em vez de 2, no nosso caso:

ks = [1, 2, 3, 4, 5 , 6 , 7 , 8, 9, 10]
plt.plot(ks, wcss);
plt.axvline(3, linestyle='--', color='r')

Podemos executar o algoritmo de cluster K-Means novamente, para ver como nossos dados ficariam com três grupos:

kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(points)
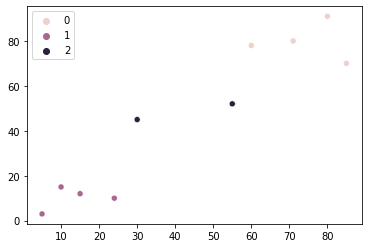
sns.scatterplot(x = points[:,0], y = points[:,1], hue=kmeans.labels_)

Já estávamos satisfeitos com dois clusters, mas de acordo com o método do cotovelo, três clusters seriam mais adequados para nossos dados. Nesse caso, teríamos três tipos de lojas em vez de duas. Antes de usar o método do cotovelo, pensávamos nos clusters de lojas do sudoeste e nordeste, agora também temos lojas no centro. Talvez esse possa ser um bom local para abrir outra loja, pois teria menos concorrência nas proximidades.

Medidas alternativas de qualidade do cluster

Há também outras medidas que podem ser usadas ao avaliar a qualidade do cluster:

• Pontuação da Silhueta – analisa não apenas a distância entre os pontos intra-cluster, mas também entre os próprios clusters
• Entre Clusters Soma de Quadrados (BCSS) – métrica complementar ao WCSS
• Erro de soma de quadrados (SSE)
• Raio Máximo – mede a maior distância de um ponto ao seu centróide
• Raio médio – a soma da maior distância de um ponto ao seu centroide dividido pelo número de clusters.

Recomenda-se experimentar e conhecer cada um deles, pois dependendo do problema, algumas das alternativas podem ser mais aplicáveis ​​do que as métricas mais utilizadas (Pontuação WCSS e Silhouette).

No final, como acontece com muitos algoritmos de ciência de dados, queremos reduzir a variação dentro de cada cluster e maximizar a variação entre diferentes clusters. Portanto, temos clusters mais definidos e separáveis.

Aplicando K-Means em outro conjunto de dados

Vamos usar o que aprendemos em outro conjunto de dados. Desta vez, tentaremos encontrar grupos de vinhos semelhantes.

Começamos importando pandas para ler o wine-clustering CSV (Valores Separados Por Virgula) arquivo em um Dataframe estrutura:

import pandas as pd

df = pd.read_csv('wine-clustering.csv')

Depois de carregá-lo, vamos dar uma olhada nos primeiros cinco registros de dados com o head() método:

df.head()

Isto resulta em:

	Alcohol 	Malic_Acid 	Ash 	Ash_Alcanity 	Magnesium 	Total_Phenols 	Flavanoids 	Nonflavanoid_Phenols 	Proanthocyanins 	Color_Intensity 	Hue 	OD280 	Proline
0 	14.23 		1.71 		2.43 	15.6 			127 		2.80 			3.06 		0.28 					2.29 				5.64 				1.04 	3.92 	1065
1 	13.20 		1.78 		2.14 	11.2 			100 		2.65 			2.76 		0.26 					1.28 				4.38 				1.05 	3.40 	1050
2 	13.16 		2.36 		2.67 	18.6 			101 		2.80 			3.24 		0.30 					2.81 				5.68 				1.03 	3.17 	1185
3 	14.37 		1.95 		2.50 	16.8 			113 		3.85 			3.49 		0.24 					2.18 				7.80 				0.86 	3.45 	1480
4 	13.24 		2.59 		2.87 	21.0 			118 		2.80 			2.69 		0.39 					1.82 				4.32 				1.04 	2.93 	735

Temos muitas medições de substâncias presentes nos vinhos. Aqui, também não precisaremos transformar colunas categóricas porque todas elas são numéricas. Agora, vamos dar uma olhada nas estatísticas descritivas com o describe() método:

df.describe().T 

A tabela de descrição:

 						count 	mean 		std 		min 	25% 	50% 	75% 		max
Alcohol 				178.0 	13.000618 	0.811827 	11.03 	12.3625 13.050 	13.6775 	14.83
Malic_Acid 				178.0 	2.336348 	1.117146 	0.74 	1.6025 	1.865 	3.0825 		5.80
Ash 					178.0 	2.366517 	0.274344 	1.36 	2.2100 	2.360 	2.5575 		3.23
Ash_Alcanity 			178.0 	19.494944 	3.339564 	10.60 	17.2000 19.500 	21.5000 	30.00
Magnesium 				178.0 	99.741573 	14.282484 	70.00 	88.0000 98.000 	107.0000 	162.00
Total_Phenols 			178.0 	2.295112 	0.625851 	0.98 	1.7425 	2.355 	2.8000 		3.88
Flavanoids 				178.0 	2.029270 	0.998859 	0.34 	1.2050 	2.135 	2.8750 		5.08
Nonflavanoid_Phenols 	178.0 	0.361854 	0.124453 	0.13 	0.2700 	0.340 	0.4375 		0.66
Proanthocyanins 		178.0 	1.590899 	0.572359 	0.41 	1.2500 	1.555 	1.9500 		3.58
Color_Intensity 		178.0 	5.058090 	2.318286 	1.28 	3.2200 	4.690 	6.2000 		13.00
Hue 					178.0 	0.957449 	0.228572 	0.48 	0.7825 	0.965 	1.1200 		1.71
OD280 					178.0 	2.611685 	0.709990 	1.27 	1.9375 	2.780 	3.1700 		4.00
Proline 				178.0 	746.893258 	314.907474 	278.00 	500.500 673.500 985.0000 	1680.00

Ao olhar para a tabela, fica claro que há alguns variabilidade nos dados – para algumas colunas, como Alchool há mais, e para outros, como Malic_Acid, menos. Agora podemos verificar se existem nullou NaN valores em nosso conjunto de dados:

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 13 columns):
 #   Column                Non-Null Count  Dtype  
---  ------                --------------  -----  
 0   Alcohol               178 non-null    float64
 1   Malic_Acid            178 non-null    float64
 2   Ash                   178 non-null    float64
 3   Ash_Alcanity          178 non-null    float64
 4   Magnesium             178 non-null    int64  
 5   Total_Phenols         178 non-null    float64
 6   Flavanoids            178 non-null    float64
 7   Nonflavanoid_Phenols  178 non-null    float64
 8   Proanthocyanins       178 non-null    float64
 9   Color_Intensity       178 non-null    float64
 10  Hue                   178 non-null    float64
 11  OD280                 178 non-null    float64
 12  Proline               178 non-null    int64  
dtypes: float64(11), int64(2)
memory usage: 18.2 KB

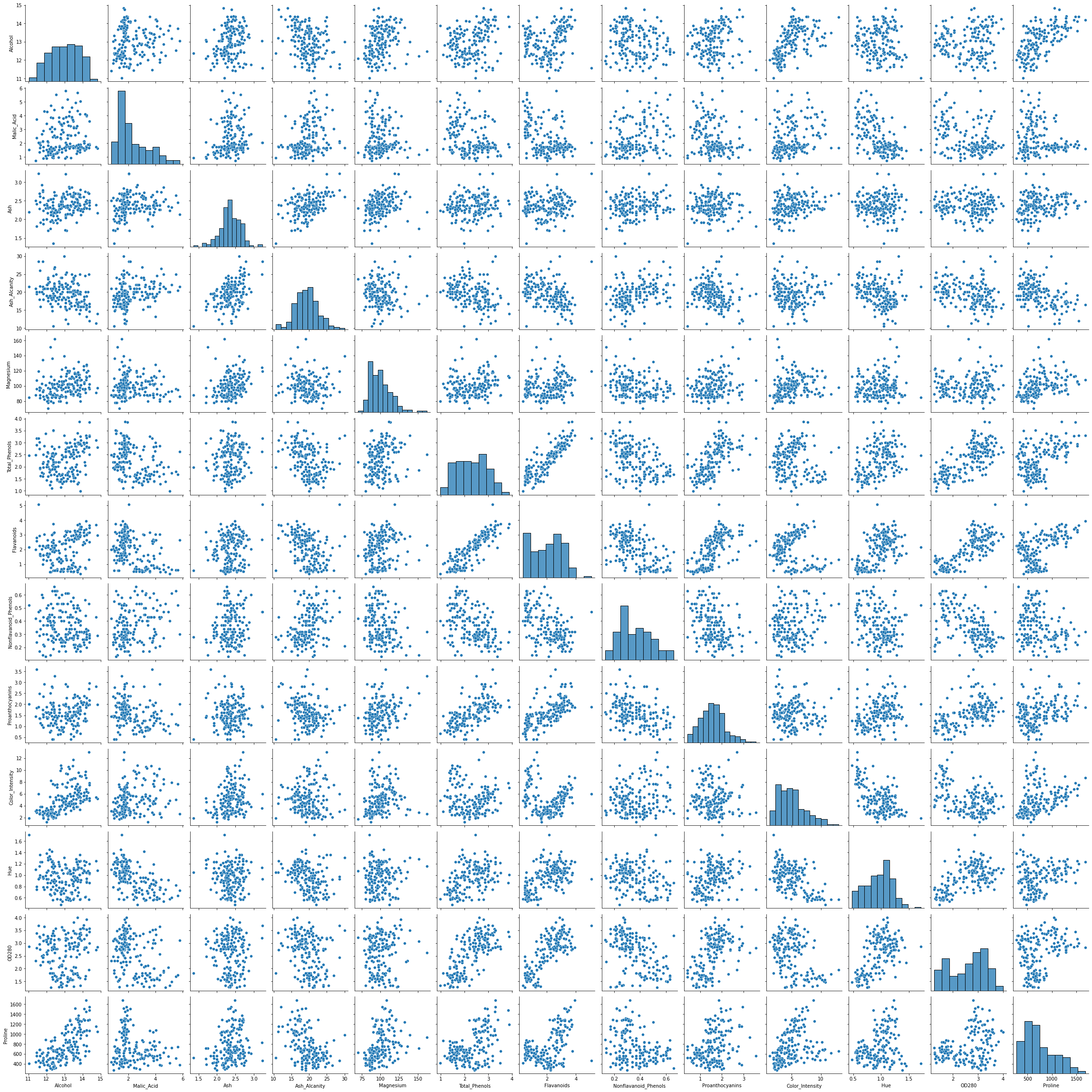
Não há necessidade de descartar ou inserir dados, considerando que não há valores vazios no conjunto de dados. Podemos usar um Seaborn pairplot() para ver a distribuição dos dados e verificar se o dataset forma pares de colunas que podem ser interessantes para clustering:

sns.pairplot(df)

Ao olhar para o pairplot, duas colunas parecem promissoras para fins de agrupamento – Alcohol e OD280 (que é um método para determinar a concentração de proteínas nos vinhos). Parece que existem 3 clusters distintos em parcelas combinando dois deles.

Existem outras colunas que parecem estar em correlação também. Mais notavelmente Alcohol e Total_Phenols e Alcohol e Flavanoids. Eles têm ótimas relações lineares que podem ser observadas no gráfico de pares.

Como nosso foco é agrupar com K-Means, vamos escolher um par de colunas, digamos Alcohol e OD280e teste o método de cotovelo para este conjunto de dados.

Vamos plotar o gráfico de dispersão com essas duas colunas definidas como seu eixo para dar uma olhada nos pontos que queremos dividir em grupos:

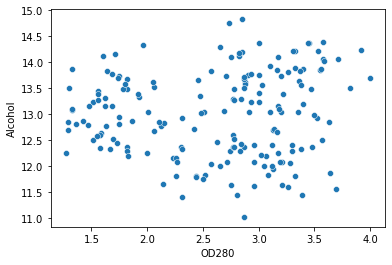
sns.scatterplot(data=df, x='OD280', y='Alcohol')

Agora podemos definir nossas colunas e usar o método do cotovelo para determinar o número de clusters. Também iniciaremos o algoritmo com kmeans++ apenas para ter certeza de que converge mais rapidamente:

values = df[['OD280', 'Alcohol']]

wcss_wine = [] 
for i in range(1, 11): 
    kmeans = KMeans(n_clusters = i, init = 'k-means++', random_state = 42)
    kmeans.fit(values) 
    wcss_wine.append(kmeans.inertia_)

Calculamos o WCSS, para que possamos plotar os resultados:

clusters_wine = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
plt.plot(clusters_wine, wcss_wine)
plt.axvline(3, linestyle='--', color='r')

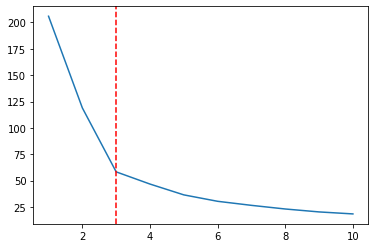
De acordo com o método do cotovelo, devemos ter 3 clusters aqui. Para a etapa final, vamos agrupar nossos pontos em 3 clusters e plotar esses clusters identificados por cores:

kmeans_wine = KMeans(n_clusters=3, random_state=42)
kmeans_wine.fit(values)
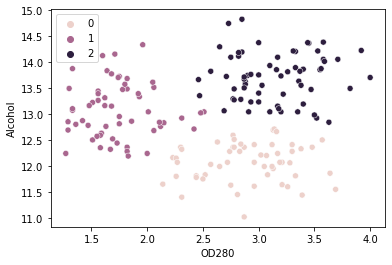
sns.scatterplot(x = values['OD280'], y = values['Alcohol'], hue=kmeans_wine.labels_)

Podemos ver aglomerados 0, 1 e 2 no gráfico. Com base em nossa análise, grupo 0 tem vinhos com maior teor de proteína e menor teor alcoólico, grupo 1 tem vinhos com maior teor alcoólico e baixo teor de proteínas, e grupo 2 tem alta proteína e alto teor alcoólico em seus vinhos.

Este é um conjunto de dados muito interessante e eu encorajo você a ir mais longe na análise agrupando os dados após a normalização e PCA – também interpretando os resultados e encontrando novas conexões.

Conclusão

K-médias clustering é um algoritmo de aprendizado de máquina não supervisionado simples, mas muito eficaz, para clustering de dados. Ele agrupa os dados com base na distância euclidiana entre os pontos de dados. O algoritmo de agrupamento K-Means tem muitos usos para agrupar documentos de texto, imagens, vídeos e muito mais.