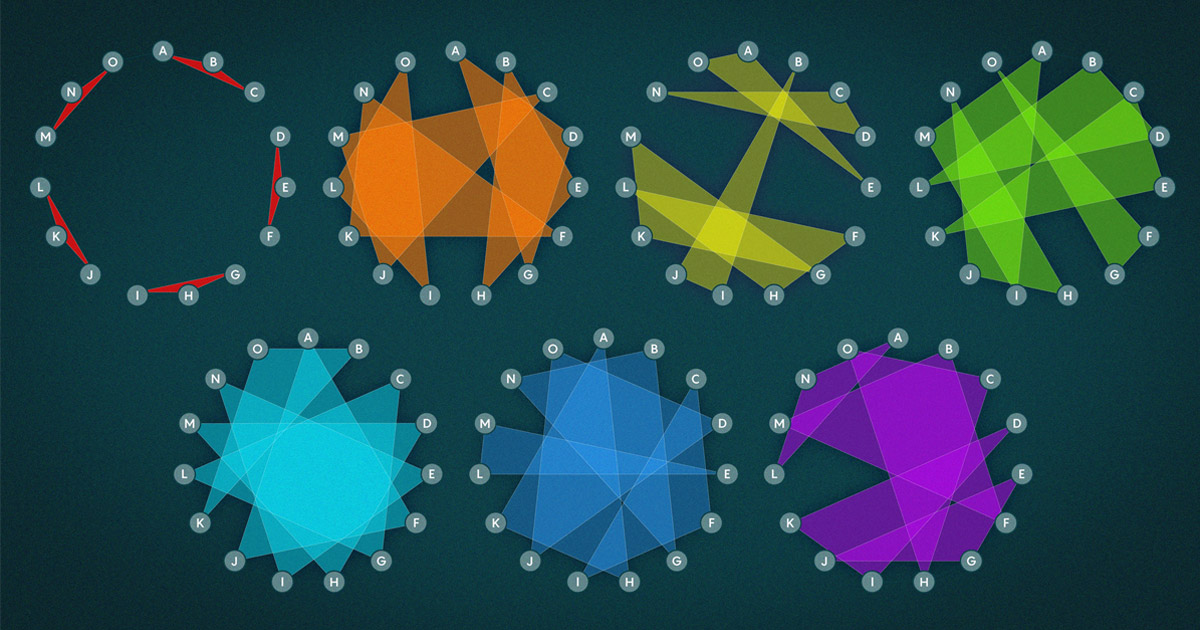
Em 1850, Thomas Penyngton Kirkman, um matemático quando não estava cumprindo sua principal responsabilidade como vigário na Igreja da Inglaterra, descreveu seu “problema de estudante”: “Quinze jovens em uma escola andam três lado a lado por sete dias consecutivos: é necessário organizar diariamente, para que dois não andem duas vezes lado a lado”.
Para um matemático moderno, este tipo de problema é melhor imaginado como um hipergrafo – um conjunto de nós reunidos em grupos de três ou mais. As 15 alunas são nós, e cada grupo de “três lado a lado” pode ser pensado como um triângulo, com três linhas, ou arestas, conectando três nós.
O problema de Kirkman pergunta essencialmente se existe um arranjo destes triângulos que liga todas as alunas umas às outras, mas com a restrição adicional de que não há dois triângulos que partilhem uma aresta. O compartilhamento de limites implicaria que duas estudantes teriam que caminhar juntas mais de uma vez. Essa restrição significa que cada garota caminha com dois novos amigos todos os dias durante uma semana, de modo que cada par possível se reúna exatamente uma vez.
Este problema e outros semelhantes têm enganado os matemáticos durante quase dois séculos desde que Kirkman colocou a sua questão. Em 1973, o lendário matemático Paul Erdős apresentou uma proposta semelhante. Ele perguntou se é possível construir um hipergrafo com duas propriedades aparentemente incompatíveis. Primeiro, cada par de nós deve ser conectado por exatamente um triângulo, como acontece com as meninas. Esta propriedade torna o gráfico denso com triângulos. O segundo requisito obriga os triângulos a se espalharem de forma muito precisa. (Especificamente, requer que para qualquer pequeno grupo de triângulos, haja pelo menos três nós a mais do que triângulos.) “Você tem esse comportamento ligeiramente contraditório quando tem um objeto geral denso que não possui partes densas”, disse David Conlon, um matemático do Instituto de Tecnologia da Califórnia.
Neste mês de janeiro, em uma prova intrincada de 50 páginas, quatro matemáticos provaram que é sempre possível construir tal hipergrafo, desde que haja nós suficientes. “A quantidade de detalhes técnicos que [eles] passaram, só para conseguir isso, foi incrível”, disse Allan Lo, um matemático da Universidade de Birmingham. Conlon concordou: “É um trabalho realmente impressionante”.
A equipe de pesquisa construiu um sistema que satisfez os requisitos diabólicos de Erdős, começando com um processo aleatório de escolha de triângulos e projetando-o com extremo cuidado para atender às suas necessidades. “O número de modificações difíceis incluídas na prova é realmente impressionante”, disse Conlon.
A estratégia deles era construir cuidadosamente o hipergrafo a partir de triângulos individuais. Por exemplo, imagine nossas 15 alunas. Desenhe uma linha entre cada par.
O objetivo aqui é traçar triângulos no topo dessas linhas de modo que os triângulos satisfaçam dois requisitos: Primeiro, não há dois triângulos que compartilhem uma aresta. (Os sistemas que atendem a esse requisito são chamados de sistemas triplos de Steiner.) E, em segundo lugar, garanta que cada pequeno subconjunto de triângulos utilize um número suficientemente grande de nós.
A maneira como os pesquisadores fizeram isso talvez seja melhor compreendida com uma analogia.
Digamos que em vez de fazer triângulos com arestas, você está construindo casas com peças de Lego. Os primeiros edifícios que você faz são extravagantes, com reforços estruturais e ornamentação elaborada. Quando terminar com eles, reserve-os. Eles servirão como um “absorvedor” – uma espécie de estoque estruturado.
Agora comece a fazer edifícios com os tijolos restantes, sem muito planejamento. Quando seu suprimento de Legos diminuir, você poderá se deparar com alguns tijolos perdidos ou casas estruturalmente defeituosas. Mas como os edifícios absorvedores são tão exagerados e reforçados, você pode arrancar alguns tijolos aqui e ali e usá-los sem cortejar a catástrofe.
No caso do sistema triplo de Steiner, você está tentando criar triângulos. Seu absorvedor, neste caso, é uma coleção de arestas cuidadosamente escolhida. Se você não conseguir classificar o resto do sistema em triângulos, poderá usar algumas das arestas que levam ao absorvedor. Então, quando terminar de fazer isso, você divide o próprio absorvedor em triângulos.
A absorção nem sempre funciona. Mas os matemáticos mexeram no processo, encontrando novas maneiras de contornar os obstáculos. Por exemplo, uma variante poderosa chamada absorção iterativa divide as arestas em uma sequência aninhada de conjuntos, de modo que cada um atue como um absorvedor para o próximo maior.
“Ao longo da última década, houve grandes melhorias”, disse Conlon. “É uma espécie de forma de arte, mas eles realmente a elevaram ao nível da arte elevada neste momento.”
O problema de Erdős era complicado mesmo com absorção iterativa. “Ficou muito claro rapidamente por que esse problema não foi resolvido”, disse Mehtaab Sawhney, um dos quatro pesquisadores que o resolveram, junto com Ashwin Sah, que junto com Sawhney é estudante de pós-graduação no Instituto de Tecnologia de Massachusetts; Michael Simkin, pós-doutorado no Centro de Ciências Matemáticas e Aplicações da Universidade de Harvard; e Mateus Kwan, matemático do Instituto de Ciência e Tecnologia da Áustria. “Havia tarefas técnicas muito interessantes e muito difíceis.”
Por exemplo, em outras aplicações de absorção iterativa, ao terminar de cobrir um conjunto - seja com triângulos, para sistemas triplos de Steiner, ou com outras estruturas para outros problemas - você pode considerá-lo resolvido e esquecê-lo. As condições de Erdős, contudo, impediram os quatro matemáticos de fazer isso. Um cluster problemático de triângulos poderia facilmente envolver nós de vários conjuntos de absorvedores.
“Um triângulo que você escolheu 500 passos atrás, você precisa de alguma forma lembrar como pensar sobre isso”, disse Sawhney.
O que os quatro finalmente descobriram foi que, se escolhessem seus triângulos com cuidado, poderiam evitar a necessidade de acompanhar cada pequena coisa. “O melhor a fazer é pensar em qualquer pequeno conjunto de 100 triângulos e garantir que esse conjunto de triângulos seja escolhido com a probabilidade correta”, disse Sawhney.
Os autores do novo artigo estão otimistas de que sua técnica possa ser estendida além deste problema. Eles têm já aplicaram sua estratégia para um problema sobre Quadrados latinos, que são como uma simplificação de um quebra-cabeça sudoku.
Além disso, existem várias questões que podem eventualmente ceder aos métodos de absorção, disse Kwan. “Há tantos problemas em combinatória, especialmente na teoria do design, onde os processos aleatórios são uma ferramenta realmente poderosa.” Um desses problemas, a conjectura de Ryser-Brualdi-Stein, também trata de quadrados latinos e aguarda solução desde a década de 1960.
Embora a absorção possa precisar de mais desenvolvimento antes de resolver esse problema, ela percorreu um longo caminho desde a sua criação, há 30 anos, disse Maya Stein, vice-diretor do Centro de Modelagem Matemática da Universidade do Chile. “Isso é algo realmente ótimo de ver, como esses métodos evoluem.”