1ICFO-Institut de Ciencies Fotoniques, Instituto de Ciência e Tecnologia de Barcelona, 08860 Castelldefels, Espanha
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Espanha
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, França
4ICREA-Institucio Catalana de Recerca i Estudis Avançados, Lluis Companys 23, 08010 Barcelona, Espanha
Acha este artigo interessante ou deseja discutir? Scite ou deixe um comentário no SciRate.
Sumário
Bases mutuamente imparciais correspondem a pares de medidas altamente úteis na teoria da informação quântica. Na menor dimensão composta, seis, sabe-se que existem entre três e sete bases mutuamente imparciais, com uma conjectura de décadas, conhecida como conjectura de Zauner, afirmando que existem no máximo três. Aqui abordamos a conjectura de Zauner numericamente através da construção de desigualdades de Bell para cada par de inteiros $n,d ge 2$ que podem ser violados ao máximo na dimensão $d$ se e somente se $n$ MUBs existirem nessa dimensão. Assim, transformamos a conjectura de Zauner em um problema de otimização, que abordamos por meio de três métodos numéricos: otimização gangorra, programação semidefinida não linear e técnicas de Monte Carlo. Todos os três métodos identificam corretamente os casos conhecidos em dimensões baixas e todos sugerem que não existem quatro bases mutuamente imparciais na dimensão seis, com todos encontrando as mesmas bases que otimizam numericamente a desigualdade de Bell correspondente. Além disso, esses otimizadores numéricos parecem coincidir com as “quatro bases mais distantes” na dimensão seis, encontradas através da otimização numérica de uma medida de distância em [P. Raynal, X. Lü, B.-G. Englert, {Fis. Rev. A}, {83} 062303 (2011)]. Por fim, os resultados de Monte Carlo sugerem que existem no máximo três MUBs na dimensão dez.
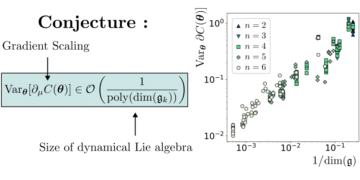
Imagem em destaque: A diferença relativa entre o valor de nossas desigualdades de Bell assumindo que existem n MUBs na dimensão d e o valor encontrado por nossos métodos numéricos. Valores zero significam que os métodos encontraram n MUBs na dimensão d, enquanto valores diferentes de zero significam que os métodos não encontraram n MUBs na dimensão d. Todos os casos conhecidos (dimensões dois a cinco e dimensão seis com dois e três MUBs) são identificados corretamente pelos números. Na dimensão seis, nenhum dos métodos encontra quatro MUBs, e todos os métodos convergem para o mesmo conjunto de quatro bases.
Resumo popular
Apesar de sua ampla utilização, ainda permanecem questões em aberto sobre a estrutura dos MUBs. Mais proeminentemente, o número máximo de medições que são imparciais aos pares (“o número de MUBs”) é desconhecido se a dimensão do sistema quântico for um número composto. Em particular, na dimensão seis sabemos apenas que o número de MUBs está entre três e sete. Uma conjectura aberta de longa data é a de Zauner, afirmando que não existem mais de três MUBs na dimensão seis. Esta conjectura de décadas é apoiada por algumas evidências numéricas, mas não existe nenhuma prova até hoje.
Neste trabalho abordamos a conjectura de Zauner através da não localidade de Bell. A não localidade de Bell diz respeito a dois experimentadores que não têm permissão para se comunicar, mas podem compartilhar algumas correlações na forma de aleatoriedade clássica ou um estado quântico compartilhado. Foi demonstrado que o compartilhamento de recursos quânticos pode levar a dados experimentais que não podem ser explicados pela física clássica (mais precisamente, pelos chamados modelos de variáveis ocultas locais). Isso é conhecido como teorema de Bell, e foi verificado experimentalmente na última década. Testemunhar a não-classicidade dos dados experimentais é mais comumente feito através das chamadas desigualdades de Bell, que são funções das probabilidades dos resultados da medição que ocorrem no experimento. Os dados clássicos devem satisfazer as desigualdades de Bell, enquanto os dados quânticos podem violá-las.
Recentemente, foram encontradas desigualdades de Bell que são violadas ao máximo se uma das partes empregar um par de medidas MUB de uma dada dimensão. Neste trabalho, estendemos essas desigualdades para novas, violadas ao máximo por um número selecionado de medidas MUB em uma dada dimensão. Além disso, se a dimensão no experimento for fixa, a violação máxima é obtida se e somente se as medidas empregadas corresponderem ao número selecionado de MUBs na dimensão dada. Portanto, decidir se um número selecionado de MUBs existe em uma determinada dimensão é equivalente a encontrar a violação máxima da desigualdade de Bell correspondente nessa dimensão fixa.
Embora encontrar essa violação máxima seja em geral um problema difícil, empregamos três métodos numéricos diferentes na tentativa de encontrar a violação máxima de nossas desigualdades de Bell em uma dimensão fixa. Dois desses métodos são variantes de técnicas de programação semidefinida, enquanto o terceiro é inspirado na física estatística e é chamado de recozimento simulado. Embora todos esses métodos sejam heurísticos - ou seja, não há garantia de que eles encontrarão o verdadeiro ótimo do problema -, pode-se avaliar seu desempenho aplicando-os a problemas de otimização cujo ótimo é conhecido. Em particular, descobrimos que todos os três métodos são capazes de identificar corretamente as medições de MUB nos casos em que se sabe que existem. Além disso, nos casos em que se sabe que não existem, todos os três métodos convergem para o mesmo conjunto de medidas até a precisão numérica. Em seguida, aplicamos nossos métodos ao primeiro caso desconhecido, ou seja, quatro MUBs na dimensão seis. Nenhum dos métodos é capaz de identificar quatro MUBs na dimensão seis, mas novamente todos convergem para o mesmo conjunto de quatro medidas com precisão numérica. Além disso, a técnica de recozimento simulado não encontra quatro MUBs na próxima dimensão composta, dimensão dez. Portanto, enquanto afirmações rigorosas não podem ser feitas devido à natureza heurística de nossas técnicas, nossos resultados suportam a conjectura de Zauner a partir da nova perspectiva da não localidade de Bell.
► dados BibTeX
► Referências
[1] ID Ivanovic. Descrição geométrica da determinação do estado quântico. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Criptografia quântica: distribuição de chave pública e lançamento de moedas. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Criptografia quântica baseada no teorema de Bell. Física Rev. Lett., 67:661-663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruss. Espionagem ótima em criptografia quântica com seis estados. Física Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques e Mohamed Bourennane. Códigos de acesso aleatório quântico usando sistemas únicos de nível $d$. Física Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas e Jędrzej Kaniewski. Bases mutuamente imparciais de autoteste no cenário de preparação e medição. Física Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci e N. Gisin. Desigualdade de Bell para qunits com medidas binárias. Informações quânticas. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos e Remigiusz Augusiak. Máxima não localidade de emaranhamento máximo e bases mutuamente imparciais e auto-teste de sistemas quânticos de dois qutrits. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal e Jędrzej Kaniewski. Bases mutuamente imparciais e medições completas informacionalmente simétricas em experimentos de Bell. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson e Karol Życzkowski. Em bases mutuamente imparciais. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K Wootters e Brian D Fields. Determinação de estado ideal por medições mutuamente imparciais. Annals of Physics, 191(2):363-381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan e Thomas Beth. Nova construção de bases mutuamente imparciais em dimensões quadradas. Informações quânticas. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Mihály Weiner. Uma lacuna para o número máximo de bases mutuamente imparciais. Proc. Amer. Matemática. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Tese de Doutorado, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep e Pawel Wocjan. Bases mutuamente imparciais e decomposições ortogonais de álgebras de Lie. Informações quânticas. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley e Stefan Weigert. Construindo bases mutuamente imparciais na dimensão seis. Física Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi e Mihály Weiner. Um problema de Pauli generalizado e uma família infinita de trigêmeos MUB na dimensão 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, maio de 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer e Afaq Tahir. Evidência a favor e contra a conjectura MUB de Zauner em $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling e Sven Polak. Bases mutuamente imparciais: otimização polinomial e simetria. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej e Karol Życzkowski. Bases mutuamente imparciais e matrizes de Hadamard de ordem seis. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü e Berthold-Georg Englert. Bases mutuamente imparciais em seis dimensões: As quatro bases mais distantes. Física Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz e Marcin Pawłowski. Conexões entre bases mutuamente imparciais e códigos de acesso aleatório quântico. Física Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani e Stephanie Wehner. Não localidade de Bell. Rev. Mod. Phys., 86: 419–478, 2014. doi: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. API MOSEK Fusion para C++ 9.2.49, 2021. URL: https://docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe e Kouhei Harada. Um método de ponto interior primal-dual para programação semidefinida não linear. Programação matemática, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd e Lieven Vandenberghe. Otimização convexa. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt e MP Vecchi. Otimização por recozimento simulado. Science, 220(4598):671-680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller e Edward Teller. Equação de cálculos de estado por máquinas de computação rápida. The Journal of Chemical Physics, 21(6):1087-1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio, and Antonio Acín. Delimitando o conjunto de correlações quânticas. Física Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Citado por
Este artigo é publicado na Quantum sob o Atribuição 4.0 do Creative Commons Internacional (CC BY 4.0) licença. Os direitos autorais permanecem com os detentores originais, como os autores ou suas instituições.