Notație Big O și analiză de algoritm cu exemple Python

Introducere

De obicei, există mai multe moduri de a rezolva problema folosind un program de calculator. De exemplu, există mai multe modalități de a sorta elementele dintr-o matrice – le puteți utiliza fuzionează sort, sortare cu bule, sortare inserție, si asa mai departe. Toți acești algoritmi au propriile lor argumente pro și contra și sarcina dezvoltatorului este să-i cântărească pentru a putea alege cel mai bun algoritm de utilizat în orice caz de utilizare. Cu alte cuvinte, întrebarea principală este ce algoritm să folosești pentru a rezolva o anumită problemă atunci când există mai multe soluții la problemă.

Analiza algoritmului se referă la analiza complexității diferiților algoritmi și găsirea celui mai eficient algoritm pentru a rezolva problema în cauză. Notație Big-O este o măsură statistică utilizată pentru a descrie complexitatea algoritmului.

În acest ghid, vom face mai întâi o scurtă trecere în revistă a analizei algoritmului și apoi vom arunca o privire mai profundă asupra notației Big-O. Vom vedea cum poate fi folosită notația Big-O pentru a găsi complexitatea algoritmului cu ajutorul diferitelor funcții Python.

De ce este importantă analiza algoritmului?

Pentru a înțelege de ce este importantă analiza algoritmului, vom lua ajutorul unui exemplu simplu. Să presupunem că un manager dă o sarcină celor doi dintre angajații săi să proiecteze un algoritm în Python care calculează factorialul unui număr introdus de utilizator. Algoritmul dezvoltat de primul angajat arată astfel:

def fact(n):
    product = 1
    for i in range(n):
        product = product * (i+1)
    return product

print(fact(5))

Observați că algoritmul ia pur și simplu un număr întreg ca argument. În interiorul fact() funcţionează o variabilă numită product este initializat la 1. O buclă se execută de la 1 la n iar în timpul fiecărei iterații, valoarea în product este înmulțit cu numărul repetat de buclă și rezultatul este stocat în product variabilă din nou. După ce bucla se execută, product variabila va conține factorialul.

În mod similar, al doilea angajat a dezvoltat și un algoritm care calculează factorialul unui număr. Al doilea angajat a folosit o funcție recursivă pentru a calcula factorialul numărului n:

def fact2(n):
    if n == 0:
        return 1
    else:
        return n * fact2(n-1)

print(fact2(5))

Managerul trebuie să decidă ce algoritm să folosească. Pentru a face acest lucru, au decis să aleagă ce algoritm rulează mai repede. O modalitate de a face acest lucru este găsirea timpului necesar pentru a executa codul pe aceeași intrare.

În blocnotesul Jupyter, puteți utiliza %timeit literal urmat de apelul funcției pentru a găsi timpul necesar funcției pentru a se executa:

%timeit fact(50)

Aceasta ne va oferi:

9 µs ± 405 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Ieșirea spune că algoritmul ia 9 microsecunde (plus/minus 45 nanosecunde) pe buclă.

În mod similar, putem calcula cât timp durează executarea celei de-a doua abordări:

%timeit fact2(50)

Aceasta va avea ca rezultat:

15.7 µs ± 427 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

Al doilea algoritm care implică recursiunea ia 15 microsecunde (plus/minus 427 nanosecunde).

Timpul de execuție arată că primul algoritm este mai rapid în comparație cu al doilea algoritm care implică recursiunea. Când aveți de-a face cu intrări mari, diferența de performanță poate deveni mai semnificativă.

Cu toate acestea, timpul de execuție nu este o măsură bună pentru a măsura complexitatea unui algoritm, deoarece depinde de hardware. Este necesară o metrică de analiză a complexității mai obiectivă pentru un algoritm. Aici este locul Notație O mare vine să joace.

Analiză algoritmică cu notație Big-O

Notația Big-O semnifică relația dintre intrarea în algoritm și pașii necesari pentru a executa algoritmul. Este notat cu un „O” mare urmat de o paranteză de deschidere și de închidere. În paranteză, relația dintre intrare și pașii parcurși de algoritm este prezentată folosind „n”.

Principala concluzie este – Big-O nu este interesat de a special instanță în care rulați un algoritm, cum ar fi fact(50), ci mai degrabă, cât de bine face scară dată de intrare în creștere. Aceasta este o măsură mult mai bună pentru evaluare decât timpul concret pentru o instanță concretă!

De exemplu, dacă există un relație liniară între intrare și pasul făcut de algoritm pentru a-și finaliza execuția, notația Big-O folosită va fi O (n). În mod similar, notația Big-O pentru funcții pătratice is O(n²).

Pentru a construi intuiția:

• O (n): la n=1, se face 1 pas. La n=10, se fac 10 pași.
• O(n²): la n=1, se face 1 pas. La n=10, se fac 100 pași.

At n=1, acești doi ar face la fel! Acesta este un alt motiv pentru care observarea relației dintre intrare și numărul de pași pentru a procesa acea intrare este mai bună decât doar evaluarea funcțiilor cu o intrare concretă.

Următoarele sunt câteva dintre cele mai comune funcții Big-O:

Nume si Prenume	O mare
Constant	O (c)
Liniar	O (n)
patratice	O(n²)
cub	O(n³)
Exponențială	O(2ⁿ)
Logaritmic	O (log (n))
Log Linear	O(nlog(n))

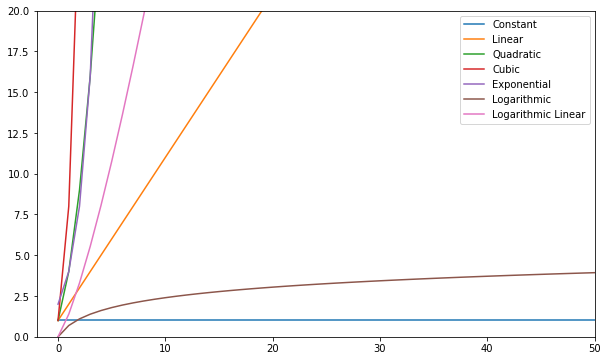
Puteți vizualiza aceste funcții și le puteți compara:

În general, orice lucru mai rău decât liniar este considerat o complexitate proastă (adică ineficient) și ar trebui evitat dacă este posibil. Complexitatea liniară este în regulă și de obicei un rău necesar. Logaritmicul este bun. Constant este uimitor!

Pentru a vă face o idee despre cum este calculat un Big-O, să aruncăm o privire la câteva exemple de complexitate constantă, liniară și pătratică.

Complexitate constantă - O(C)

Se spune că complexitatea unui algoritm este constantă dacă pașii necesari pentru a finaliza execuția unui algoritm rămân constanți, indiferent de numărul de intrări. Complexitatea constantă este notă prin O (c) Unde c poate fi orice număr constant.

Să scriem un algoritm simplu în Python care găsește pătratul primului element din listă și apoi îl imprimă pe ecran:

def constant_algo(items):
    result = items[0] * items[0]
    print(result)

constant_algo([4, 5, 6, 8])

În scenariul de mai sus, indiferent de dimensiunea intrării, sau numărul de articole din lista de intrare items, algoritmul efectuează doar 2 pași:

1. Aflarea pătratului primului element
2. Imprimarea rezultatului pe ecran.

Prin urmare, complexitatea rămâne constantă.

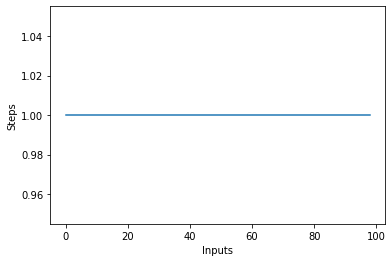
Dacă desenați un grafic cu linii cu dimensiunea variabilă a items introduceți pe axa X și numărul de pași pe axa Y, veți obține o linie dreaptă. Să creăm un scurt script care să ne ajute să vizualizăm acest lucru. Indiferent de numărul de intrări, numărul de pași executați rămâne același:

steps = []
def constant(n):
    return 1
    
for i in range(1, 100):
    steps.append(constant(i))
plt.plot(steps)

Complexitate liniară - O (n)

Se spune că complexitatea unui algoritm este liniară dacă pașii necesari pentru a finaliza execuția unui algoritm cresc sau descresc liniar cu numărul de intrări. Complexitatea liniară se notează prin O (n).

În acest exemplu, să scriem un program simplu care afișează toate elementele din listă pe consolă:

def linear_algo(items):
    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Complexitatea linear_algo() funcția este liniară în exemplul de mai sus, deoarece numărul de iterații al buclei for va fi egală cu dimensiunea intrării items mulțime. De exemplu, dacă există 4 elemente în items listă, bucla for va fi executată de 4 ori.

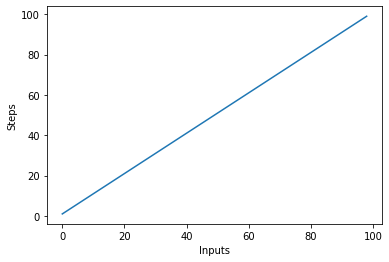
Să creăm rapid o diagramă pentru algoritmul de complexitate liniară cu numărul de intrări pe axa x și numărul de pași pe axa y:

steps = []
def linear(n):
    return n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

Aceasta va avea ca rezultat:

Un lucru important de remarcat este că, cu intrări mari, constantele tind să-și piardă din valoare. Acesta este motivul pentru care în mod obișnuit eliminăm constante din notația Big-O, iar o expresie precum O(2n) este de obicei scurtată la O(n). Atât O(2n) cât și O(n) sunt liniare – relația liniară este cea care contează, nu valoarea concretă. De exemplu, să modificăm linear_algo():

def linear_algo(items):
    for item in items:
        print(item)

    for item in items:
        print(item)

linear_algo([4, 5, 6, 8])

Există două bucle for care iterează peste intrare items listă. Prin urmare, complexitatea algoritmului devine O (2n), cu toate acestea, în cazul elementelor infinite din lista de intrare, dublul infinitului este în continuare egal cu infinitul. Putem ignora constanta 2 (deoarece este în cele din urmă nesemnificativ) și complexitatea algoritmului rămâne O (n).

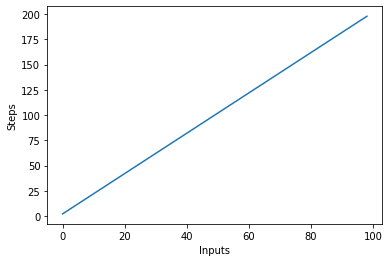
Să vizualizăm acest nou algoritm graficând intrările pe axa X și numărul de pași pe axa Y:

steps = []
def linear(n):
    return 2*n
    
for i in range(1, 100):
    steps.append(linear(i))
    
plt.plot(steps)
plt.xlabel('Inputs')
plt.ylabel('Steps')

În scriptul de mai sus, puteți vedea clar asta y=2n, cu toate acestea, ieșirea este liniară și arată astfel:

Complexitate pătratică - O(n²)

Se spune că complexitatea unui algoritm este pătratică atunci când pașii necesari pentru a executa un algoritm sunt o funcție pătratică a numărului de elemente din intrare. Complexitatea pătratică este notă ca O(n²):

def quadratic_algo(items):
    for item in items:
        for item2 in items:
            print(item, ' ' ,item2)

quadratic_algo([4, 5, 6, 8])

Avem o buclă exterioară care iterează prin toate elementele din lista de intrare și apoi o buclă interioară imbricată, care iterează din nou prin toate elementele din lista de intrare. Numărul total de pași efectuati este n*n, unde n este numărul de elemente din tabloul de intrare.

Următorul grafic prezintă numărul de intrări în raport cu pașii pentru un algoritm cu complexitate pătratică:

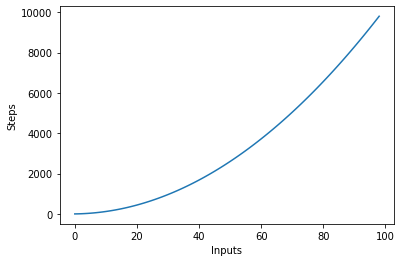
Complexitatea logaritmică - O (logn)

Unii algoritmi ating o complexitate logaritmică, cum ar fi Căutare binară. Căutare binară caută un element dintr-o matrice, bifând de mijloc a unei matrice și tăierea jumătății în care nu se află elementul. Face acest lucru din nou pentru jumătatea rămasă și continuă aceiași pași până când elementul este găsit. În fiecare pas, acesta jumatati numărul de elemente din matrice.

Acest lucru necesită sortarea matricei și pentru noi să facem o presupunere despre date (cum ar fi că sunt sortate).

Când puteți face ipoteze despre datele primite, puteți lua măsuri care reduc complexitatea unui algoritm. Complexitatea logaritmică este de dorit, deoarece atinge performanțe bune chiar și cu intrare la scară ridicată.

Găsirea complexității funcțiilor complexe?

În exemplele anterioare, aveam funcții destul de simple la intrare. Totuși, cum calculăm Big-O al funcțiilor care apelează (mai multe) alte funcții pe intrare?

Să aruncăm o privire:

def complex_algo(items):

    for i in range(5):
        print("Python is awesome")

    for item in items:
        print(item)

    for item in items:
        print(item)

    print("Big O")
    print("Big O")
    print("Big O")

complex_algo([4, 5, 6, 8])

În scriptul de mai sus sunt efectuate mai multe sarcini, mai întâi, un șir este imprimat de 5 ori pe consolă folosind print afirmație. În continuare, imprimăm lista de intrare de două ori pe ecran și, în final, un alt șir este imprimat de trei ori pe consolă. Pentru a găsi complexitatea unui astfel de algoritm, trebuie să descompunăm codul algoritmului în părți și să încercăm să găsim complexitatea pieselor individuale. Notați complexitatea fiecărei piese.

În prima secțiune avem:

for i in range(5):
	print("Python is awesome")

Complexitatea acestei părți este O (5) deoarece în această bucată de cod sunt efectuate cinci pași constanti, indiferent de intrare.

În continuare, avem:

for item in items:
	print(item)

Știm că complexitatea piesei de cod de mai sus este O (n). În mod similar, complexitatea următoarei bucăți de cod este de asemenea O (n):

for item in items:
	print(item)

În cele din urmă, în următoarea bucată de cod, un șir este tipărit de trei ori, deci complexitatea este O (3):

print("Big O")
print("Big O")
print("Big O")

Pentru a găsi complexitatea generală, trebuie pur și simplu să adăugăm aceste complexități individuale:

O(5) + O(n) + O(n) + O(3)

Simplificand cele de mai sus obtinem:

O(8) + O(2n) = O(8+2n)

Am spus mai devreme că atunci când intrarea (care are lungimea n în acest caz) devine extrem de mare, constantele devin nesemnificative, adică de două ori sau jumătate din infinit rămâne infinit. Prin urmare, putem ignora constantele. Complexitatea finală a algoritmului va fi O (n)!

Complexitatea celui mai rău și cel mai bun caz

De obicei, când cineva vă întreabă despre complexitatea unui algoritm - este interesat de complexitatea cazului cel mai rău (Big-O). Uneori, ar putea fi interesați și de complexitatea celui mai bun caz (Big-Omega).

Pentru a înțelege relația dintre acestea, să aruncăm o privire la o altă bucată de cod:

def search_algo(num, items):
    for item in items:
        if item == num:
            return True
        else:
            pass
nums = [2, 4, 6, 8, 10]

print(search_algo(2, nums))

În scriptul de mai sus, avem o funcție care ia ca intrare un număr și o listă de numere. Returnează adevărat dacă numărul trecut este găsit în lista de numere, în caz contrar, revine None. Dacă căutați 2 în listă, acesta va fi găsit în prima comparație. Aceasta este cea mai bună complexitate a algoritmului, prin aceea că elementul căutat este găsit în primul index căutat. Cel mai bun caz de complexitate, în acest caz, este O (1). Pe de altă parte, dacă căutați 10, acesta va fi găsit la ultimul index căutat. Algoritmul va trebui să caute prin toate elementele din listă, prin urmare complexitatea celui mai rău caz devine O (n).

Pe lângă complexitatea celui mai bun și cel mai rău caz, puteți și calcula complexitatea medie (Big-Theta) a unui algoritm, care vă spune „dată o intrare aleatorie, care este complexitatea de timp așteptată a algoritmului”?

Complexitatea spațială

Pe lângă complexitatea timpului, în care numărați numărul de pași necesari pentru a finaliza execuția unui algoritm, puteți găsi și complexitatea spațiului care se referă la cantitatea de spațiu pe care trebuie să o alocați în memorie în timpul execuției unui program.

Aruncă o privire la următorul exemplu:

def return_squares(n):
    square_list = []
    for num in n:
        square_list.append(num * num)

    return square_list

nums = [2, 4, 6, 8, 10]
print(return_squares(nums))

return_squares() funcția acceptă o listă de numere întregi și returnează o listă cu pătratele corespunzătoare. Algoritmul trebuie să aloce memorie pentru același număr de articole ca în lista de intrare. Prin urmare, complexitatea spațială a algoritmului devine O (n).

Concluzie

Notația Big-O este metrica standard utilizată pentru a măsura complexitatea unui algoritm. În acest ghid, am studiat ce este notația Big-O și cum poate fi utilizată pentru a măsura complexitatea unei varietăți de algoritmi. De asemenea, am studiat diferite tipuri de funcții Big-O cu ajutorul diferitelor exemple Python. În cele din urmă, am analizat pe scurt complexitatea celui mai rău și cel mai bun caz, împreună cu complexitatea spațiului.