Modelul de amestec al procesului Dirichlet

• 23 Iunie, 2014
• Vasilis Vryniotis
• . 2 comentarii

Această postare de blog este a patra parte a seriei despre Clustering cu modele de amestec de proces Dirichlet. În articolele anterioare am discutat despre modelele de amestecuri Dirichlet finite și am luat limita modelului lor pentru grupuri infinite de k, ceea ce ne-a condus la introducerea proceselor Dirichlet. După cum am văzut, ținta noastră este să construim un model de amestec care nu ne cere să specificăm numărul de k clustere/componente de la început. După prezentând diferite reprezentări ale Proceselor Dirichlet, acum este timpul să folosim efectiv DP-urile pentru a construi un model de amestec infinit care ne permite să realizăm clustering. Scopul acestui articol este de a defini modelele de amestec de proces Dirichlet și de a discuta despre utilizarea procesului de restaurant chinezesc și a eșantionării Gibbs. Dacă nu ați citit postările anterioare, este foarte recomandat să faceți acest lucru deoarece subiectul este puțin teoretic și necesită o bună înțelegere asupra construcției modelului.

Actualizare: Datumbox Machine Learning Framework este acum open-source și gratuit Descarca. Consultați pachetul com.datumbox.framework.machinelearning.clustering pentru a vedea implementarea modelelor Dirichlet Process Mixture în Java.

1. Definirea modelului de amestec de proces Dirichlet

Utilizarea proceselor Dirichlet ne permite să avem un model de amestec cu componente infinite care poate fi considerat ca luând limita modelului finit pentru k la infinit. Să presupunem că avem următorul model:

Ecuația 1: Modelul amestecului procesului Dirichlet

Unde G este definit ca și folosit ca notaţie scurtă pentru care este o funcție delta care ia 1 dacă si 0 in alta parte. θ_i sunt parametrii cluster care sunt eșantionați din G. Distribuția generativă F este configurată de parametrii cluster θ_i și este folosit pentru a genera x_i observatii. În cele din urmă putem defini o distribuție de densitate care este distribuția noastră de amestec (amestec infinit numărabil) cu proporții de amestecare și amestecarea componentelor .

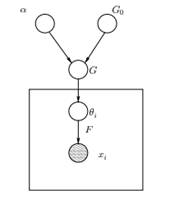
Figura 1: Modelul grafic al modelului de amestec de proces Dirichlet

Mai sus putem vedea modelul grafic echivalent al DPMM. G₀ este distribuția de bază a DP și este de obicei selectată pentru a fi conjugată înainte de distribuția noastră generativă F pentru a ușura calculele și a utiliza proprietățile matematice atrăgătoare. α este hiperparametrul scalar al procesului Dirichlet și afectează numărul de clustere pe care le vom obține. Cu cât valoarea lui α este mai mare, cu atât clusterele sunt mai multe; cu cât α este mai mic, cu atât mai puține clustere. Ar trebui să remarcăm că valoarea lui α exprimă puterea de a crede în G₀. O valoare mare indică faptul că majoritatea probelor vor fi distincte și vor avea valori concentrate pe G₀. G este o distribuție aleatorie pe spațiul parametrilor Θ eșantionat din DP care atribuie probabilități parametrilor. θ_i este un vector de parametri care este extras din distribuția G și conține parametrii clusterului, distribuția F este parametrizată de θ_i și x_i este punctul de date generat de distribuția generativă F.

Este important de reținut că θ_i sunt elemente ale spațiului parametrilor Θ și „configurează” clusterele noastre. Ele pot fi văzute și ca variabile latente pe x_i care ne spun din ce componentă/cluster x_i provine și care sunt parametrii acestei componente. Astfel pentru fiecare x_i pe care le observăm, desenăm un θ_i din distribuția G. La fiecare tragere, distribuția se schimbă în funcție de selecțiile anterioare. După cum am văzut în schema de urne Blackwell-MacQueen, distribuția G poate fi integrată și viitoarele noastre selecții de θ_i depinde doar de G₀: . Estimarea parametrilor θi din formula anterioară nu este întotdeauna fezabilă deoarece multe implementări (cum ar fi Procesul restaurantului chinezesc) implică enumerarea prin intermediul k componente crescând exponențial. Astfel, sunt utilizate metode de calcul aproximative, cum ar fi eșantionarea Gibbs. În cele din urmă, ar trebui să remarcăm că, deși k clustere sunt infinite, numărul de clustere active este . Astfel θ_i se va repeta și va prezenta un efect de grupare.

2. Utilizarea procesului de restaurant chinezesc pentru a defini un model de amestec infinit

Modelul definit în segmentul anterior este solid din punct de vedere matematic, totuși are un dezavantaj major: pentru fiecare x nou_i pe care le observăm, trebuie să eșantionăm un nou θ_i luând în considerare valorile anterioare ale lui θ. Problema este că, în multe cazuri, eșantionarea acestor parametri poate fi o sarcină dificilă și costisitoare din punct de vedere computațional.

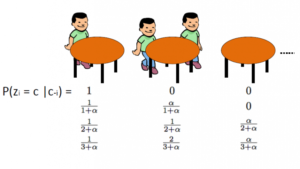
O abordare alternativă este utilizarea procesului restaurantului chinezesc pentru a modela variabilele latente z_i de atribuiri de cluster. În acest fel, în loc să folosiți θ_i pentru a desemna atât parametrii clusterului, cât și atribuirile clusterului, folosim variabila latentă z_i pentru a indica ID-ul clusterului și apoi utilizați această valoare pentru a atribui parametrii clusterului. Ca rezultat, nu mai trebuie să eșantionăm un θ de fiecare dată când obținem o nouă observație, ci în schimb obținem atribuirea clusterului prin eșantionarea z_i de la CRP. Cu această schemă, un nou θ este eșantionat numai atunci când trebuie să creăm un nou cluster. Mai jos vă prezentăm modelul acestei abordări:

Ecuația 2: Model de amestec cu CRP

Cel de mai sus este un model generativ care descrie modul în care datele x_i iar clusterele sunt generate. Pentru a efectua analiza cluster trebuie să folosim observațiile x_i și estimați atribuirile cluster z_i.

3. Inferența modelului de amestec și eșantionarea Gibbs

Din păcate, deoarece procesele Dirichlet sunt neparametrice, noi nu pot folosi algoritmul EM pentru a estima variabilele latente care stochează atribuirile clusterului. Pentru a estima sarcinile vom folosi Eșantionare Gibbs prăbușită.

Eșantionarea Gibbs restrânsă este un algoritm simplu Markov Chain Monte Carlo (MCMC). Este rapid și ne permite să integrăm unele variabile în timp ce eșantionăm o altă variabilă. Cu toate acestea, acest algoritm ne cere să selectăm un G₀ care este un anterior conjugat al distribuției generative F pentru a putea rezolva analitic ecuațiile și a putea eșantiona direct din .

Pașii eșantionării Gibbs restrânse pe care îi vom folosi pentru a estima atribuirile clusterului sunt următorii:

• Inițializați z_i atribuiri ale grupului aleatoriu
• Repetați până la convergență
• Selectați la întâmplare ax_i
  
• Păstrați celălalt z_j fix pentru fiecare j≠i:
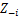
• Atribuiți o nouă valoare pentru z_i prin calcularea „probabilității CRP” care depinde de z_j și x_j din toate j≠i:

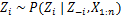
În articolul următor ne vom concentra asupra modului de efectuare a analizei cluster folosind modelele de amestec de proces Dirichlet. Vom defini două modele diferite de amestec de proces Dirichlet care utilizează Procesul restaurant chinezesc și Eșantionarea Gibbs restrânsă pentru a realiza gruparea pe seturi de date și documente continue.