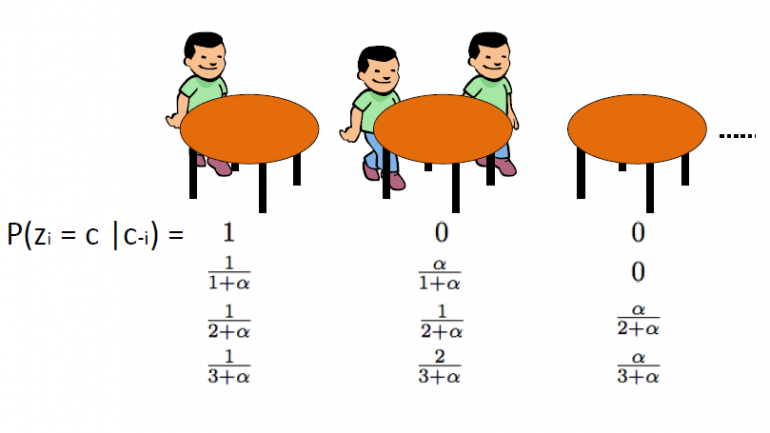Procesul Dirichlet Procesul restaurantului chinezesc și alte reprezentări

• 20 Mai, 2014
• Vasilis Vryniotis
• . Fara comentarii

Acest articol este a treia parte a seriei despre Clustering with Dirichlet Process Mixture Models. Data anterioară am definit modelul de amestec finit bazat pe distribuția Dirichlet și am pus întrebări despre cum putem face acest model infinit infinit. Am discutat pe scurt ideea de a lua limita modelului atunci când numărul k de clustere tinde spre infinit, dar așa cum am subliniat, existența unui astfel de obiect nu este banală (cu alte cuvinte, cum „luăm de fapt limita unui model ”?). Ca o reamintire, motivul pentru care dorim să luăm make k infinit este că în acest fel vom avea un model neparametric care nu ne cere să predefinim numărul total de clustere din date.

Actualizare: Datumbox Machine Learning Framework este acum open-source și gratuit Descarca. Consultați pachetul com.datumbox.framework.machinelearning.clustering pentru a vedea implementarea modelelor Dirichlet Process Mixture în Java.

Chiar dacă ținta noastră este să construim un model care să fie capabil să realizeze clustering pe seturi de date, înainte de asta trebuie să discutăm despre Procesele Dirichlet. Vom oferi atât definițiile matematice stricte, cât și explicațiile mai intuitive ale DP și vom discuta modalități de construire a procesului. Acele construcții/reprezentări pot fi văzute ca o modalitate de a găsi apariții ale Procesului Dirichlet în „viața reală”.

În ciuda faptului că am încercat să-mi adaptez raportul de cercetare în așa fel încât aceste postări pe blog să fie mai ușor de urmărit, este totuși important să definim instrumentele și distribuțiile matematice necesare înainte de a trece la utilizarea modelelor. Modelele procesului Dirichlet sunt un subiect de cercetare activă, dar necesită o bună înțelegere a statisticii și proceselor stocastice înainte de a le utiliza. O altă problemă este că, după cum vom vedea în acest articol, Procesele Dirichlet pot fi reprezentate/construite prin numeroase moduri. Ca rezultat, mai multe lucrări academice folosesc notații/convenții complet diferite și examinează problema din puncte de vedere diferite. În această postare încerc să le explic cât mai simplu și să folosesc aceeași notație. Sperăm că lucrurile vor deveni mai clare odată cu cele două articole viitoare care se concentrează pe definirea modelelor de amestec de proces Dirichlet și asupra modului de utilizare efectivă a acestora pentru a efectua analiza cluster.

1. Definiția procesului Dirichlet

Un proces Dirichlet pe un spațiu Θ este un proces stocastic. Este o distribuție de probabilitate pe „distribuții de probabilitate pe spațiul Θ” și a extrage din el este o distribuție discretă. Mai formal, o distribuție Dirichlet este o distribuție pe măsuri de probabilitate. A măsură de probabilitate este o funcție de submulțimi de spațiu Θ la [0,1]. G este o măsură de probabilitate aleatorie distribuită DP, notat ca , dacă pentru orice partiție (A₁,…A_n) din spațiul Θ avem că .

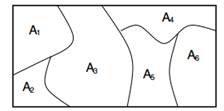
Figura 1: Marginale pe partițiile finite sunt distribuite Dirichlet.

DP are doi parametri: Primul este distribuția de bază G₀ care servește ca un mijlociu . Al doilea este parametrul de rezistență α care este strict pozitiv și servește ca varianță inversă . Determină gradul de repetare a valorilor distribuției de ieșire. Cu cât valoarea lui a este mai mare, cu atât repetiția este mai mică; cu cât valoarea este mai mică, cu atât este mai mare repetarea valorilor distribuției ieșirii. În cele din urmă, spațiul Θ este spațiul parametrilor pe care definim DP. Mai mult, spațiul Θ este și spațiul de definiție al lui G₀ care este același cu cel al lui G.

Un mai simplu și mai mult mod intuitiv pentru a explica un proces Dirichlet este următorul. Să presupunem că avem un spațiu Θ care poate fi împărțit în orice mod finit (A₁,…,A_n) și o distribuție de probabilitate G care le atribuie probabilități. G este o distribuție de probabilitate specifică pe Θ, dar există multe altele. Procesul Dirichlet pe Θ modelează exact acest lucru; este o distribuție peste toate distribuțiile de probabilitate posibile pe spațiul Θ. Procesul Dirichlet este parametrizat cu G₀ funcția de bază și parametrul de concentrație α. Putem spune că G este distribuit conform DP cu parametrii α și G₀ dacă distribuția comună a probabilităților pe care G le atribuie partițiilor lui Θ urmează distribuția Dirichlet. Alternativ, putem spune că probabilitățile pe care G le atribuie oricărei partiții finite a lui Θ urmează distribuția Dirichlet.

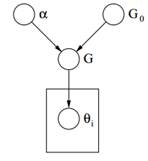
Figura 2: Modelul grafic al procesului Dirichlet

În cele din urmă, mai sus putem vedea modelul grafic al unui DP. Ar trebui să remarcăm că α este un hiperparametru scalar, G₀ este distribuția de bază a DP, G o distribuție aleatorie pe spațiul parametrilor Θ eșantionat din DP care atribuie probabilități parametrilor și θ_i este un vector parametru care este extras din distribuția G și este un element al spațiului Θ.

2. Procesele Dirichlet posterioare

Procesele posterioare Dirichlet au fost discutate de Ferguson. Începem prin a desena o măsură aleatorie de probabilitate G dintr-un proces Dirichlet, . Deoarece G este o distribuție de probabilitate pe Θ, putem de asemenea să eșantionăm din această distribuție și să extragem eșantioane independente distribuite identic θ₁,…, θ_n ~ G. Deoarece extragerile dintr-un Proces Dirichlet sunt distribuții discrete, putem reprezenta Unde este o notație scurtă pentru care este o funcție delta care ia 1 dacă si 0 in alta parte. Un efect interesant al acestui lucru este că, deoarece G este definit în acest fel, există o probabilitate pozitivă ca diferite eșantioane să aibă aceeași valoare. . După cum vom vedea mai târziu, acest lucru creează un efect de grupare care poate fi utilizat pentru a efectua analiza clusterului pe seturile de date.

Folosind definițiile și observațiile de mai sus dorim să estimăm posteriorul Procesului Dirichlet având în vedere probele θ. Cu toate acestea, din moment ce știm asta și folosind Regulile Bayes și Conjugația dintre Dirichlet și Multinomial avem că și .

Ecuația 1: Procesul Dirichlet posterior

Această proprietate este foarte importantă și este utilizată de diferitele reprezentări DP.

3. Reprezentări ale procesului Dirichlet

În segmentele anterioare am definit Procesul Dirichlet și am prezentat modelul său teoretic. O întrebare importantă la care trebuie să răspundem este cum știm că un astfel de obiect există și cum putem construi si reprezenta un proces Dirichlet.

Primele indicii de existență au fost furnizate de Ferguson care a folosit Teorema de consistență Kolmogorov, a dat definiția unui proces Dirichlet și a descris Procesul Dirichlet posterior. Continuându-și cercetările, Blackwell și MacQueen a folosit teorema lui de Finetti pentru a demonstra existența unei astfel de măsurători aleatoare de probabilitate și a introdus schema urnei Blackwell-MacQueen care satisface proprietățile procesului Dirichlet. În 1994 Sethuraman a oferit un mod suplimentar simplu și direct de a construi un DP prin introducerea construcției Stick-breaking. În cele din urmă, o altă reprezentare a fost oferită de Aldous care a introdus Procesul Restaurantului Chinezesc ca o modalitate eficientă de a construi un Proces Dirichlet.

Diferitele reprezentări ale procesului Dirichlet sunt echivalente din punct de vedere matematic, dar formularea lor diferă deoarece examinează problema din puncte de vedere diferite. Mai jos prezentăm cele mai comune reprezentări găsite în literatură și ne concentrăm pe Procesul Restaurantului Chinezesc, care oferă o modalitate simplă și eficientă din punct de vedere computațional de a construi algoritmi de inferență pentru Procesul Dirichlet.

3.1 Schema de urne Blackwell-MacQueen

Schema de urne Blackwell-MacQueen poate fi folosită pentru a reprezenta un proces Dirichlet și a fost introdusă de Blackwell și MacQueen. Se bazează pe schema urnei Pólya, care poate fi văzută ca modelul opus de eșantionare fără înlocuire. În schema urnei Pólya presupunem că avem o urnă netransparentă care conține bile colorate și tragem bile la întâmplare. Cand tragem o bila, ii observam culoarea, o punem inapoi in urna si adaugam o bila suplimentara de aceeasi culoare. O schemă similară este folosită de Blackwell și MacQueen pentru a construi un proces Dirichlet.

Această schemă produce o secvență de θ₁,θ₂,… cu probabilități condiționate . În această schemă presupunem că G₀ este o distribuție pe culori și fiecare θ_n reprezintă culoarea mingii care se pune în urnă. The Algoritmul este după cum urmează:

· Începem cu o urna goală.

· Cu probabilitate proporțională cu α noi desenăm si adaugam o bila de aceasta culoare in urna.

· Cu probabilitate proporțională cu n-1 extragem o minge aleatorie din urnă, îi observăm culoarea, o așezăm înapoi în urnă și adăugăm o minge suplimentară de aceeași culoare în urnă.

Anterior, am început cu un proces Dirichlet și am derivat schema Blackwell-MacQueen. Acum să începem invers de la schema Blackwell-MacQueen și să derivăm DP. Deoarece θ_i au fost trase într-o manieră iid din G, distribuția lor comună va fi invariantă la orice permutări finite și astfel sunt interschimbabile. În consecință, folosind teorema lui de Finetti, avem că trebuie să existe o distribuție peste măsuri pentru a le face iid și această distribuție este Procesul Dirichlet. Ca rezultat, demonstrăm că schema urnei Blackwell-MacQueen este o reprezentare a DP și ne oferă o modalitate concretă de a o construi. După cum vom vedea mai târziu, această schemă este echivalentă matematic cu Procesul Restaurantului Chinezesc.

3.2 Construcția de rupere a bastonului

Construcția Stick-breaking este o modalitate alternativă de a reprezenta un proces Dirichlet care a fost introdus de Sethuraman. Este un mod constructiv de a forma distribuție și folosește urmand analogia: Presupunem ca avem un bat de lungime 1, il spargem in pozitia β₁ și atribuim π₁ egală cu lungimea părții de băț pe care am rupt-o. Repetăm ​​același proces pentru a obține π₂, Pi₃,… etc; datorită modului în care este definită această schemă, putem continua să o facem de nenumărate ori.

Pe baza celor de mai sus, π_k poate fi modelat ca , În cazul în care în timp ce, ca și în schemele anterioare, θ sunt eșantionate direct de distribuția de bază . În consecință, distribuția G poate fi scrisă ca o sumă de funcții delta ponderate cu π_k probabilități care este egală cu . Astfel, construcția Stick-breaking ne oferă o modalitate simplă și intuitivă de a construi un Proces Dirichlet.

3.3 Procesul restaurantului chinezesc

Procesul restaurantului chinezesc, care a fost introdus de Aldous, este o altă modalitate eficientă de a reprezenta un proces Dirichlet și poate fi direct legată de schema de urne Blackwell-MacQueen. Această schemă folosește urmand analogia: Presupunem că există un restaurant chinezesc cu multe mese infinite. Pe măsură ce clienții intră în restaurant, se așează aleatoriu la oricare dintre mesele ocupate sau aleg să se așeze la prima masă liberă disponibilă.

CRP definește o distribuție pe spațiul partițiilor numerelor întregi pozitive. Începem prin a desena θ₁,…θ_n din schema de urne Blackwell-MacQueen. După cum am discutat în segmentele anterioare, ne așteptăm să vedem un efect de grupare și astfel numărul total de valori unice θ k va fi semnificativ mai mic decât n. Astfel, aceasta definește o partiție a mulțimii {1,2,…,n} în k clustere. În consecință, extragerea din schema de urne Blackwell-MacQueen induce o partiție aleatorie a setului {1,2,...,n}. Procesul restaurantului chinezesc este indus de aceasta distribuție pe partiții. Algoritmul este următorul:

· Începem cu un restaurant gol.

· 1^st clientul stă mereu pe 1^st tabel

· n+1^th clientul are 2 variante:

o Stați la prima masă neocupată cu probabilitate

o Așezați-vă pe oricare dintre cele XNUMX-a mese ocupate cu probabilitate
Unde este numărul de oameni care stau pe acea masă

Unde α este valoarea de dispersie a DP și n este numărul total de clienți din restaurant la un moment dat. Variabila latentă z_i stochează numărul de tabel al i^th client și ia valori de la 1 la k_n unde k_n este numărul total de mese ocupate când n clienți sunt în restaurant. Ar trebui să remarcăm că k_n va fi întotdeauna mai mic sau egal cu n și în medie este de aproximativ . În cele din urmă ar trebui să remarcăm că probabilitatea de aranjare a tabelului este invariant la permutări. Astfel, z_i este interschimbabil, ceea ce implică faptul că tabelele cu aceeași dimensiune a clienților au aceeași probabilitate.

Procesul Restaurantului Chinezesc este strâns legat de schema de urne Pólya și Procesul Dirichlet. CRP este o modalitate de a specifica a distribuție pe partiții (atribuții de tabel) de n puncte și poate fi folosit ca a priori pe spațiul variabilei latente z_i care determină atribuirile clusterului. CRP este echivalent cu schema de urnă a lui Pólya, cu doar diferența că nu atribuie parametri fiecărei tabele/cluster. A merge de la CRP la schema de urne a lui Pólya noi desenăm pentru toate tabelele k=1,2... și apoi pentru fiecare x_i care este grupată în tabelul z_i atribuie a . Cu alte cuvinte, atribuiți noului x_i parametrul θ al tabelului. În sfârșit de când nu putem atribui de la θ la mesele infinite de la început, putem doar să atribuim un nou θ de fiecare dată când cineva se așează pe o masă nouă. Datorită tuturor celor de mai sus, CRP ne poate ajuta să construim algoritmi eficienți din punct de vedere computațional pentru a efectua analiza cluster pe seturi de date.

În această postare, am discutat despre Procesul Dirichlet și despre câteva modalități de a-l construi. Vom folosi ideile de mai sus în articolul următor. Vom introduce Modelul de amestec al procesului Dirichlet și vom folosi Reprezentarea restaurantului chinezesc pentru a construi Procesul Dirichlet și analiza clusterului de preforme. Dacă ați ratat câteva puncte, nu vă faceți griji, deoarece lucrurile vor începe să devină mai clare cu următoarele două articole.

Sper că ați găsit această postare interesantă. Dacă ați făcut-o, acordați-vă un moment pentru a o distribui pe Facebook și Twitter. 🙂