1ICFO-Institut de Ciencies Fotoniques, Institutul de Știință și Tehnologie din Barcelona, 08860 Castelldefels, Spania
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spania
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Franța
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spania
Găsiți această lucrare interesant sau doriți să discutați? Scite sau lasă un comentariu la SciRate.
Abstract
Baze imparțial reciproc corespund perechilor de măsurători extrem de utile în teoria informației cuantice. În cea mai mică dimensiune compozită, șase, se știe că există între trei și șapte baze reciproc imparțial, cu o conjectura veche de zeci de ani, cunoscută sub numele de conjectura lui Zauner, care afirmă că există cel mult trei. Aici abordăm numeric conjectura lui Zauner prin construirea inegalităților Bell pentru fiecare pereche de numere întregi $n,d ge 2$ care pot fi încălcate maxim în dimensiunea $d$ dacă și numai dacă $n$ MUB există în acea dimensiune. Prin urmare, transformăm conjectura lui Zauner într-o problemă de optimizare, pe care o abordăm prin intermediul a trei metode numerice: optimizarea see-saw, programarea semidefinită neliniară și tehnicile Monte Carlo. Toate cele trei metode identifică corect cazurile cunoscute în dimensiuni mici și toate sugerează că nu există patru baze reciproc imparțial în dimensiunea șase, toate găsind aceleași baze care optimizează numeric inegalitatea Bell corespunzătoare. Mai mult, acești optimizatori numerici par să coincidă cu „cele mai îndepărtate patru baze” din dimensiunea șase, găsite prin optimizarea numerică a unei măsuri de distanță în [P. Raynal, X. Lü, B.-G. Englert, {Fiz. Rev. A}, { 83} 062303 (2011)]. În cele din urmă, rezultatele Monte Carlo sugerează că cel mult trei MUB-uri există în dimensiunea zece.
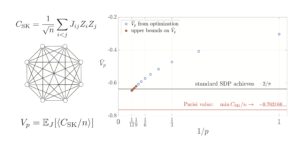
Imagine prezentată: Diferența relativă dintre valoarea inegalităților noastre Bell presupunând că n MUB-uri există în dimensiunea d și valoarea găsită prin metodele noastre numerice. Valorile zero înseamnă că metodele au găsit n MUB-uri în dimensiunea d, în timp ce valorile diferite de zero înseamnă că metodele nu au găsit n MUB-uri în dimensiunea d. Toate cazurile cunoscute (dimensiunile două până la cinci și dimensiunea șase cu două și trei MUB) sunt corect identificate prin cifre. În dimensiunea șase, niciuna dintre metode nu găsește patru MUB-uri și toate metodele converg către același set de patru baze.
Rezumat popular
În ciuda utilizării lor pe scară largă, rămân încă întrebări deschise cu privire la structura MUB-urilor. Cel mai important, numărul maxim de măsurători care sunt imparțial în perechi („numărul de MUB”) este necunoscut dacă dimensiunea sistemului cuantic este un număr compus. În special, în dimensiunea șase știm doar că numărul de MUB este între trei și șapte. O presupunere deschisă de lungă durată este cea a lui Zauner, care afirmă că nu există mai mult de trei MUB-uri în dimensiunea șase. Această presupunere de zeci de ani este susținută de unele dovezi numerice, dar nu există nicio dovadă până în prezent.
În această lucrare abordăm conjectura lui Zauner prin non-localitatea Bell. Non-localitatea Bell se referă la doi experimentatori care nu au voie să comunice, dar pot împărtăși unele corelații sub forma aleatoriei clasice sau a unei stări cuantice partajate. S-a demonstrat că partajarea resurselor cuantice poate duce la date experimentale care nu pot fi explicate prin fizica clasică (mai precis, prin așa-numitele modele de variabile ascunse locale). Aceasta este cunoscută sub numele de teorema lui Bell și a fost verificată experimental în ultimul deceniu. Observarea neclasicității datelor experimentale se face cel mai frecvent prin așa-numitele inegalități Bell, care sunt funcții ale probabilităților de rezultat al măsurării care apar în experiment. Datele clasice trebuie să satisfacă inegalitățile Bell, în timp ce datele cuantice le pot încălca.
Recent, s-au descoperit inegalități Bell care sunt încălcate maxim dacă una dintre părți folosește o pereche de măsurători MUB de o anumită dimensiune. În această lucrare, extindem aceste inegalități la altele noi, încălcate maxim de un număr selectat de măsurători MUB într-o anumită dimensiune. Mai mult, dacă dimensiunea din experiment este fixă, încălcarea maximă se obține dacă și numai dacă măsurătorile utilizate corespund numărului selectat de MUB-uri în dimensiunea dată. Prin urmare, a decide dacă un număr selectat de MUB-uri există într-o anumită dimensiune este echivalent cu găsirea încălcării maxime a inegalității Bell corespunzătoare în această dimensiune fixă.
În timp ce găsirea acestei încălcări maxime este în general o problemă dificilă, folosim trei metode numerice diferite ca o încercare de a găsi încălcarea maximă a inegalităților noastre Bell într-o dimensiune fixă. Două dintre aceste metode sunt variante ale tehnicilor de programare semidefinită, în timp ce a treia este inspirată din fizica statistică și se numește recoacere simulată. Deși toate aceste metode sunt euristice - adică nu există nicio garanție că vor găsi adevăratul optim al problemei - se poate evalua performanța lor aplicând la probleme de optimizare al căror optim este cunoscut. În special, constatăm că toate cele trei metode sunt capabile să identifice corect măsurătorile MUB în cazurile în care se știe că există. În plus, în cazurile în care se știe că nu există, toate cele trei metode converg către același set de măsurători până la precizie numerică. Apoi aplicăm metodele noastre la primul caz necunoscut, adică patru MUB-uri în dimensiunea șase. Niciuna dintre metode nu este capabilă să identifice patru MUB-uri în dimensiunea șase, dar din nou toate converg către același set de patru măsurători până la precizie numerică. Mai mult, tehnica de recoacere simulată nu găsește patru MUB-uri în următoarea dimensiune compozită, dimensiunea zece. Prin urmare, în timp ce afirmațiile riguroase nu pot fi făcute din cauza naturii euristice a tehnicilor noastre, rezultatele noastre susțin conjectura lui Zauner din noua perspectivă a non-localității Bell.
► Date BibTeX
► Referințe
[1] ID Ivanovic. Descrierea geometrică a determinării stării cuantice. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Criptografia cuantică: distribuirea cheilor publice și aruncarea de monede. Proceedings of IEEE International Conference on Computers, Systems and Signal Processing (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Criptografia cuantică bazată pe teorema lui Bell. Fiz. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruß. Interceptare optimă în criptografia cuantică cu șase stări. Fiz. Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques și Mohamed Bourennane. Coduri de acces aleatoriu cuantice folosind sisteme unice de nivel $d$. Fiz. Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas și Jędrzej Kaniewski. Auto-testarea bazelor imparțiale reciproce în scenariul pregătirii și măsurării. Fiz. Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci şi N. Gisin. Inegalitate de clopot pentru qunits cu măsurători binare. Informații cuantice. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos și Remigiusz Augusiak. Non-localitate maximă din încrucișarea maximă și baze reciproc imparțiale și auto-testarea sistemelor cuantice cu doi qutriți. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal și Jędrzej Kaniewski. Baze imparțial reciproc și măsurători simetrice complete din punct de vedere informațional în experimentele Bell. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https:///doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson și Karol Życzkowski. Pe baze reciproc imparțial. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K Wootters și Brian D Fields. Determinarea optimă a stării prin măsurători imparțial reciproc. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan și Thomas Beth. Construcție nouă de baze reciproc imparțial în dimensiuni pătrate. Informații cuantice. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Mihály Weiner. Un decalaj pentru numărul maxim de baze imparțial reciproc. Proc. Amer. Matematică. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. teză de doctorat, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep și Pawel Wocjan. Baze imparțial reciproc și descompuneri ortogonale ale algebrelor Lie. Informații cuantice. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley și Stefan Weigert. Construirea unor baze imparțial reciproc în dimensiunea șase. Fiz. Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi și Mihály Weiner. O problemă Pauli generalizată și o familie infinită de tripleți MUB în dimensiunea 6. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, mai 2009. doi:10.1088/1751-8113/42/24/245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer și Afaq Tahir. Dovezi pentru și împotriva conjecturei MUB a lui Zauner în $mathbb{C}^6$. 2021. doi:10.48550/arXiv.2103.08703.
https:///doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling și Sven Polak. Baze imparțial reciproc: optimizare polinomială și simetrie. 2021. doi:10.48550/arXiv.2111.05698.
https:///doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej și Karol Życzkowski. Baze imparțial reciproc și matrici Hadamard de ordinul șase. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü și Berthold-Georg Englert. Baze imparțial reciproc în șase dimensiuni: Cele patru baze cele mai îndepărtate. Fiz. Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz și Marcin Pawłowski. Conexiuni între baze imparțial reciproc și coduri de acces aleatoriu cuantic. Fiz. Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani și Stephanie Wehner. Nonlocalitatea Bell. Rev. Mod. Phys., 86: 419–478, 2014. doi: 10.1103 / RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. MOSEK Fusion API pentru C++ 9.2.49, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe și Kouhei Harada. O metodă de punct interior primal-dual pentru programarea neliniară semidefinită. Programare matematică, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
https: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd și Lieven Vandenberghe. Optimizare convexă. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt și MP Vecchi. Optimizare prin recoacere simulată. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller și Edward Teller. Ecuația calculelor de stare prin mașini de calcul rapide. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio și Antonio Acín. Mărginirea setului de corelații cuantice. Fiz. Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Citat de
Acest Lucru este publicat în Quantum sub Creative Commons Atribuire 4.0 internațională (CC BY 4.0) licență. Drepturile de autor rămân la deținătorii de drepturi de autor originale, precum autorii sau instituțiile lor.