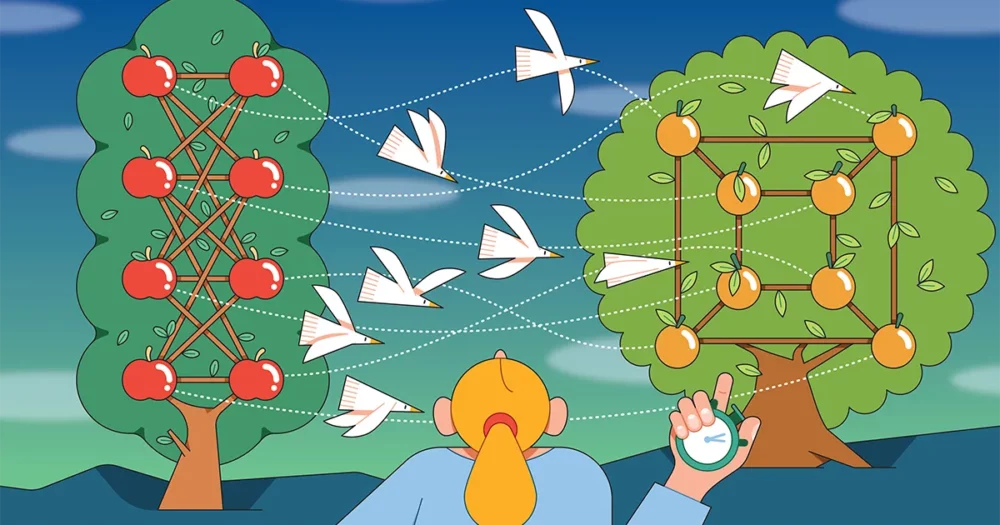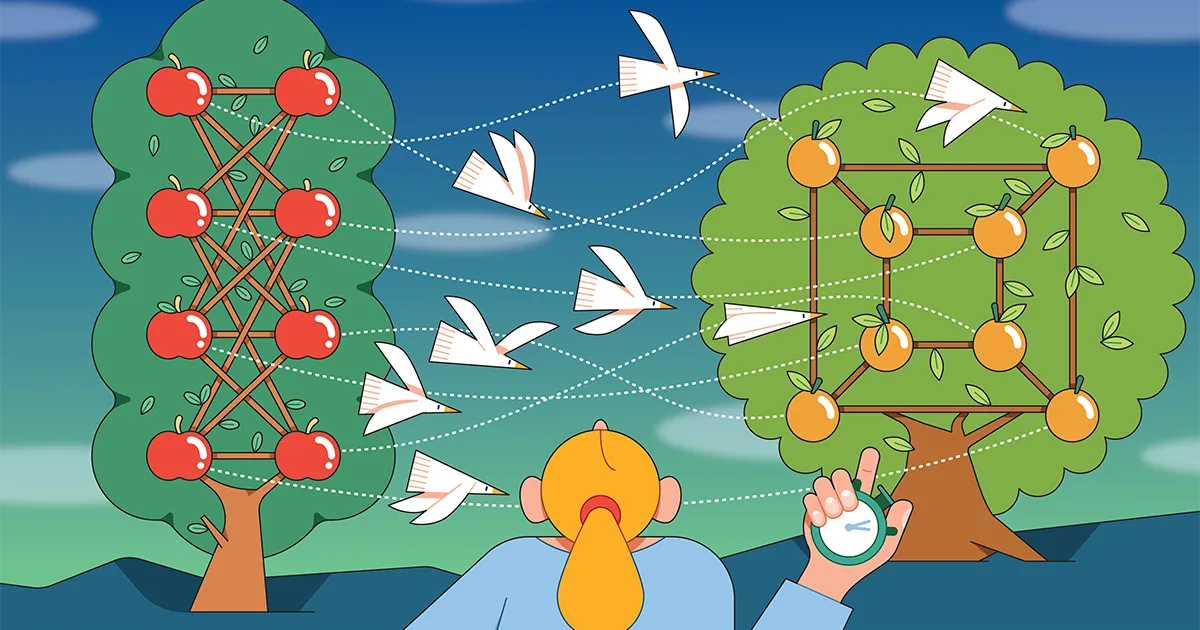
Введение
Если кто-то попросит вас определить, являются ли два объекта одинаковыми, это может показаться тривиальным запросом. В большинстве повседневных случаев достаточно беглого взгляда, чтобы вынести верное суждение.
Но в информатике это гораздо более сложный вопрос. На самом деле, это то, что затрагивает нерешенную суть того, на что способны компьютеры. В зависимости от того, что представляют собой объекты и как вы определяете одинаковость, мы все еще не знаем, могут ли компьютеры быстро ответить на вопрос, или медленный и трудоемкий подход — это, по сути, лучшее, с чем они могут справиться.
За последнее десятилетие были получены некоторые важные результаты, демонстрирующие, что компьютеры могут работать хотя бы немного лучше. Один из самые большие недавние результаты в информатике был более быстрый алгоритм для определения того, когда два графика одинаковы. Работа 2015 года, автор Ласло Бабаи Чикагского университета преодолела один важный барьер скорости вычислений, но не достигла другого.
А теперь статья Сяоруй Сан из Университета Иллинойса в Чикаго представил новый, более быстрый алгоритм для связанного вопроса, называемого проблемой группового изоморфизма, который заключается в том, чтобы узнать, когда два математических объекта, называемых группами, одинаковы. Работа, размещенная в Интернете в прошлом марте, делает небольшой шаг к прояснению базовой вычислительной сложности, связанной со сравнением объектов.
Работа Сана нарушает давнее ограничение скорости для определенного класса групп — того, который считается самым сложным для решения примером проблемы группового изоморфизма. Если алгоритм может быстро сравнивать группы такого рода, есть надежда, что он сможет быстро сравнивать группы любого типа.
«Мы не знаем такой теоремы, но у нас есть основания полагать, что что-то подобное должно быть правдой», — сказал Джош Грохов Университет Колорадо, Боулдер.
Сравнение сравнений
Чтобы точно определить, являются ли две вещи одинаковыми, вам сначала нужно определить «одинаковое». Две строки чисел могут считаться одинаковыми, если они просто содержат одни и те же цифры, или могут потребоваться одинаковые цифры в одном и том же порядке.
Изоморфизм — это особый вид одинаковости, который часто встречается в математике. Когда два объекта изоморфны друг другу, это примерно означает, что они содержат одни и те же элементы и что эти элементы находятся в одинаковых отношениях друг с другом.
Графики — наборы вершин (точек), соединенных ребрами (линиями), — обеспечивают доступный визуальный способ увидеть, как может выглядеть изоморфизм. Два графа изоморфны, если вы можете сопоставить вершины одного графа с вершинами другого, так что вершины, соединенные ребром в первом графе, соединены ребром во втором. Изоморфные графы могут выглядеть по-разному на первый взгляд, но у них общая основная структура.
Введение
Группы более абстрактны, чем графы, но их все же можно сравнивать по изоморфизму. Группа — это набор элементов, таких как числа, которые можно комбинировать друг с другом в соответствии с некоторой операцией, так что результат также находится в наборе. Например, у вас может быть группа, элементами которой являются целые числа — все положительные и отрицательные целые числа плюс ноль — и чья операция — сложение: сложите любые два целых числа, и результатом всегда будет другое целое число.
Две группы изоморфны, если вы можете соединить каждый элемент в одной группе с элементом в другой, так что результат операции над двумя элементами в первой группе согласуется с результатом операции над эквивалентными значениями этих элементов во второй группа.
Вот простой пример двух групп, каждая из которых состоит из двух элементов, изоморфных друг другу. Первая группа состоит из цифр 0 и 1, а вторая группа состоит из букв a и b. Обе группы содержат операцию объединения элементов группы определенным образом, результаты которой представлены в таблицах ниже.
Введение
Группы изоморфны, потому что 0 соединяется с a, 1 пара с b, а структурные отношения, возникающие при объединении элементов, одинаковы в обеих группах.
«Мы говорим, что две группы изоморфны, если они в основном эквивалентны», — сказал Сан.
Несбалансированный прогресс
Изоморфизм — важное понятие в математике, где широко используются графы и группы, потому что он позволяет математикам не обращать внимания на поверхностные различия и сосредоточиться на том, как связанные объекты могут быть на самом деле одинаковыми. Но это также фундаментально в компьютерных науках; исследователи не только ищут алгоритмы, которые определяют, являются ли два объекта изоморфными, но и измеряют, насколько быстро эти алгоритмы могут работать.
Это измерение может быть сложным. Скорость алгоритма зависит от того, как время его выполнения изменяется в зависимости от размера объектов, над которыми он работает. Представьте, например, что у вас есть две пары групп. В одной паре каждая группа содержит по пять элементов. В другом каждая группа содержит по 10 элементов.
Вы ожидаете, что алгоритму потребуется больше времени, чтобы определить, являются ли группы с большим количеством элементов изоморфными. Но сколько еще времени? Это займет в два раза больше времени? 52 дольше? 25 дольше? Эти вопросы соответствуют важным широким классификациям алгоритмической скорости: они могут выполняться за линейное время (что в данном случае означает, что это занимает в два раза больше времени), полиномиальное время (52 дольше) и экспоненциальное время (25 дольше).
Ученые-компьютерщики знают, к какой категории скорости относится большинство вычислительных вопросов, но не все.
«Большинство из них либо самые простые, либо самые сложные [тип вопроса], но все же есть несколько исключений, о которых ничего неизвестно», — сказал Сан. Изоморфизм графов и групп относится к числу тех исключений, что делает их такими привлекательными для изучения.
В 1970s, Роберт Тарьян из Принстонского университета понял, что существует алгоритм, который может определить, являются ли любые две группы изоморфными, со временем выполнения $latex n^{{(log,n)}}$, где n количество элементов в каждой группе. Это называется алгоритмом квазиполиномиального времени, и в иерархии сред выполнения он лучше, чем экспоненциальное время (2n), но хуже, чем полиномиальное время (n2). Это примерно такая же скорость, как у алгоритма изоморфизма графов Бабая, и это все еще лучшее, что мы можем сделать для групп почти 50 лет спустя.
«Это примерно означает, что за полвека не было никакого прогресса», — сказал Сан.
Во время получения результата Тарьяна проблема группового изоморфизма изучалась более широко, чем графовая версия. Сегодня все изменилось, отчасти потому, что изоморфизм графов стимулировал захватывающие инновации, в то время как изоморфизм групп застопорился.
«Все наши инструменты работали очень медленно в течение многих лет, и было трудно использовать то, что мы знаем об алгебре [групп]», — сказал Джеймс Уилсон Колорадского государственного университета.
Но, несмотря на это несоответствие, две проблемы имеют более глубокую связь, чем сходство их названий: проблема изоморфизма групп (по крайней мере, в этой формулировке) сводится к проблеме изоморфизма графов. Это означает, что любой алгоритм, способный решить задачу графа, может решить и групповую задачу за такое же время. Обратное неверно — прогресс по группе не означает прогресс по графу. Но отсутствие прогресса в решении проблемы групп оказало давление на математиков, стремящихся к соизмеримым достижениям в решении проблемы графов. Как вы можете выполнить более сложную задачу, если вы не можете сначала сделать что-то, что тесно связано и кажется еще более легким?
Введение
«Другими словами, — сказал Сан, — для дальнейшего улучшения изоморфизма графов изоморфизм групп является большим узким местом».
Преобразованная проблема
Когда прогресс в решении проблемы останавливается так же долго, как это было с групповым изоморфизмом, обычно требуется изобретательность, чтобы выйти из тупика. «Когда у вас большой аванс, это должно быть некоторым признаком того, что есть новая идея», — сказал Грохов.
В работе Сана содержится несколько идей, которые включают в себя нацеливание на группу важного типа и поиск умного способа разбить эти группы на части, чтобы сравнить их.
Группы, для которых работает алгоритм Солнца, называются p-группы класса 2 и экспоненты p. Они подобны группам, в которых произведение двух элементов является другим элементом, и произведение остается одним и тем же независимо от порядка их умножения. Но что действительно важно, так это то, что они представляют для общей проблемы группового изоморфизма. Эти группы имеют очень простую структуру, а значит, их должно быть легко сравнивать. Но, несмотря на эту простоту, исследователи так и не придумали, как ускорить алгоритм. Пока они не могли, казалось безнадежным внести улучшения в общий вопрос об изоморфизме групп.
Sun начала с переключения настроек с групп на матрицы, массивы чисел, которые служат базовыми объектами в линейной алгебре. Это стало возможным благодаря теореме 1930-х годов, называемой соответствием Бэра, которая превращает эту версию вопроса об изоморфизме групп в совершенно аналогичную проблему о матрицах. В частности, Сан работал с матричными пространствами, которые представляют собой наборы матриц со специальным свойством: (линейная) комбинация любых двух матриц в пространстве равняется другой матрице в пространстве.
Другими словами, эти пространства очень похожи на группы. Поэтому вместо того, чтобы пытаться понять, когда две группы изоморфны, Сан мог бы просто попытаться понять, когда два матричных пространства изометричны — понятие изоморфизма матричных пространств, которое соответствует понятию изоморфизма групп.
Сан был не первым исследователем, который применил этот подход, но он был первым, кто ввел дополнительный шаг: разбиение матричного пространства на две части. Одна часть — ядро пространства, в котором все матрицы простые. Другая часть — это пространство, окружающее это ядро, в котором все матрицы особенно сложны. Этот ход соответствует разбиению группы на подгруппы, которые содержат только некоторые из общих элементов.
Затем Сан применил различные алгоритмические методы к каждой из этих частей. Ядро имеет простую структуру, поэтому он использовал характеристику структуры, чтобы представить ее более организованным образом. Внешний слой более сложен, поэтому нет очевидного быстрого способа сравнить его с другим. Вместо этого метод Сан использует подход, называемый индивидуализацией и уточнением, чтобы исключить большинство возможных способов сопоставления одного внешнего слоя с другим, а затем использует компьютер для обработки всех оставшихся возможных способов, чтобы определить, существует ли изоморфное соответствие.
Этот метод по духу похож на то, как вы могли бы решить головоломку судоку. Есть некоторые квадраты, потенциальные значения которых ограничены тем, что вы уже знаете (ядро матричного пространства), что позволяет вам быстро их заполнить. Затем есть другие (внешний слой), которые имеют меньше ограничений, но которые вы можете выяснить, просто перепробовав все возможные значения — и пока таких квадратов не слишком много, вы все равно можете решить головоломку в разумное количество времени.
«Я заполняю все вещи, которые, как я могу быстро определить, ограничены, и теперь я могу вернуться и попробовать свое сердце на недостающих коробках», — сказал Уилсон. «Если вы сузили область, сейчас самое время переключиться и использовать компьютер для поиска правильных значений».
Открытие Сана показало, что это расщепление всегда возможно для матричных пространств, соответствующих p-группы класса 2 и экспоненты p. Затем он доказал, что после такого разделения комбинация алгоритмических методов позволяет определить, изоморфны ли два пространства в $latex n^{{(log,n)}^{5/6}}$ времени, т.е. немного ниже, чем метод Тарьяна $latex n^{{(log,n)}}$. (Оба алгоритма также включают постоянные члены, которые не оказывают большого влияния на время выполнения и которые мы опустили для ясности.)
Результат не определяет, к какому изоморфизму группы категории скорости относится; это все еще где-то между экспоненциальным и полиномиальным временем. Но Sun немного подтолкнула его к полиномиальной стороне вещей, и есть основания полагать, что возможно нечто большее. В конце концов, его работа предоставляет ученым-компьютерщикам более быстрый алгоритм группового изоморфизма для самых сложных типов групп, что повышает вероятность того, что подобное ускорение может быть достижимо для групп всех видов.
«Если вы можете решить ее за p-Группы, возможно, вы сможете решить все это, — сказал Грохов. "Может быть."
- SEO-контент и PR-распределение. Получите усиление сегодня.
- PlatoData.Network Вертикальный генеративный ИИ. Расширьте возможности себя. Доступ здесь.
- ПлатонАйСтрим. Интеллект Web3. Расширение знаний. Доступ здесь.
- ПлатонЭСГ. Автомобили / электромобили, Углерод, чистые технологии, Энергия, Окружающая среда, Солнечная, Управление отходами. Доступ здесь.
- Смещения блоков. Модернизация права собственности на экологические компенсации. Доступ здесь.
- Источник: https://www.quantamagazine.org/computer-scientists-inch-closer-to-major-algorithmic-goal-20230623/
- :имеет
- :является
- :нет
- :куда
- ][п
- $UP
- 1
- 10
- 2015
- 50
- 50 лет
- a
- О нас
- АБСТРАКТ НАЯ
- доступной
- выполнять
- По
- точный
- на самом деле
- Добавить
- дополнение
- дополнительный
- принять
- продвижение
- авансы
- После
- алгоритм
- алгоритмический
- алгоритмы
- Все
- Позволяющий
- позволяет
- уже
- причислены
- всегда
- среди
- количество
- an
- и
- Другой
- ответ
- любой
- привлекательный
- прикладной
- подхода
- примерно
- МЫ
- AS
- At
- назад
- Бэр
- барьер
- основанный
- в основном
- BE
- , так как:
- было
- начал
- верить
- ниже
- ЛУЧШЕЕ
- Лучшая
- между
- большой
- изоферменты печени
- коробки
- Ломать
- брейки
- прорыв
- широкий
- Сломался
- но
- by
- под названием
- CAN
- способный
- случаев
- случаев
- Категории
- века
- изменения
- Чикаго
- ясность
- класс
- тесно
- ближе
- лыжных шлемов
- Коллекции
- Колорадо
- сочетание
- сочетании
- комбинируя
- выходит
- сравнить
- сравнив
- сравнение
- комплекс
- сложность
- компьютер
- Информатика
- компьютеры
- вычисление
- сама концепция
- подключенный
- связи
- считается
- последовательный
- состоит
- постоянная
- ограничения
- содержать
- содержит
- Основные
- соответствующий
- соответствует
- может
- сокращение
- десятилетие
- более глубокий
- демонстрирующий
- в зависимости
- Несмотря на
- Определять
- определения
- DID
- Различия
- различный
- цифры
- do
- не
- Dont
- два
- каждый
- легче
- Простейший
- легко
- Edge
- эффект
- или
- элемент
- элементы
- достаточно
- Равно
- Эквивалент
- по существу
- Даже
- повседневный
- пример
- захватывающий
- существует
- ожидать
- Эксплуатировать
- экспоненциальный
- широко
- факт
- Осень
- Водопад
- далеко
- БЫСТРО
- быстрее
- Особенность
- несколько
- меньше
- фигура
- фигурный
- заполнять
- обнаружение
- Во-первых,
- Фокус
- Что касается
- от
- фундаментальный
- далее
- Доходы
- передач
- Общие
- получить
- взгляд
- Go
- цель
- хорошо
- график
- Графики
- группы
- Группы
- Половина
- Жесткий
- Есть
- he
- Сердце
- иерархия
- его
- надежды
- Как
- HTML
- HTTP
- HTTPS
- i
- идея
- идеи
- if
- Иллинойс
- картина
- важную
- улучшать
- улучшение
- in
- включают
- индикация
- инновации
- пример
- вместо
- в
- вводить
- Изобретение
- включать в себя
- вовлеченный
- IT
- ЕГО
- всего
- Вид
- Знать
- знание
- Отсутствие
- Фамилия
- новее
- слой
- наименее
- оставил
- такое как
- ОГРАНИЧЕНИЯ
- линий
- связанный
- мало
- журнал
- Длинное
- давнишний
- дольше
- посмотреть
- выглядит как
- серия
- ниже
- журнал
- основной
- сделать
- ДЕЛАЕТ
- управлять
- многих
- отображение
- Совпадение
- согласование
- математике
- математический
- математика
- матрица
- Вопросы
- Май..
- означает
- проводить измерение
- измерение
- просто
- метод
- методы
- может быть
- отсутствующий
- БОЛЕЕ
- самых
- двигаться
- много
- my
- имена
- необходимо
- Необходимость
- отрицательный
- Новые
- нет
- понятие
- сейчас
- номер
- номера
- объекты
- of
- on
- ONE
- онлайн
- только
- операционный
- операция
- or
- заказ
- Организованный
- Другое
- Другое
- наши
- внешний
- общий
- пара
- пар
- бумага & картон
- часть
- особый
- особенно
- мимо
- кусок
- штук
- Платон
- Платон Интеллектуальные данные
- ПлатонДанные
- плюс
- положительный
- возможность
- возможное
- размещены
- потенциал
- необходимость
- представлены
- вероятно
- Проблема
- проблемам
- Произведенный
- Продукт
- Прогресс
- собственность
- доказанный
- обеспечивать
- приводит
- головоломка
- Квантовый журнал
- вопрос
- Вопросы
- САЙТ
- быстро
- привлечение
- достигать
- реализованный
- на самом деле
- причина
- разумный
- последний
- снижает
- рассматривать
- Несмотря на
- Связанный
- отношения
- осталось
- остатки
- представлять
- запросить
- исследователь
- исследователи
- результат
- Итоги
- обратный
- правую
- грубо
- Правило
- Run
- Сказал
- то же
- сообщили
- Наука
- Ученые
- сфера
- Поиск
- Во-вторых
- посмотреть
- поиск
- казаться
- кажется
- служить
- установка
- несколько
- Поделиться
- Короткое
- должен
- сторона
- аналогичный
- просто
- простота
- Размер
- медленной
- небольшой
- So
- РЕШАТЬ
- некоторые
- Кто-то
- удалось
- где-то
- Space
- пространства
- особый
- конкретный
- скорость
- дух
- раскол
- квадраты
- Область
- Шаг
- По-прежнему
- структурный
- Структура
- структурированный
- учился
- Кабинет
- такие
- Вс
- Поверхность
- окружающих
- Коммутатор
- взять
- принимает
- направлены
- снижения вреда
- сказать
- terms
- чем
- который
- Ассоциация
- График
- Матрица
- их
- Их
- тогда
- Там.
- Эти
- они
- задача
- вещи
- этой
- те
- Через
- время
- в
- сегодня
- слишком
- инструменты
- Всего
- к
- прообразы
- правда
- стараться
- Дважды
- два
- напишите
- лежащий в основе
- понимать
- Университет
- Чикагский университет
- неизвестный
- до
- использование
- используемый
- использования
- обычно
- ценностное
- Наши ценности
- версия
- очень
- законопроект
- Путь..
- способы
- we
- WebP
- Что
- когда
- будь то
- , которые
- в то время как
- все
- чья
- широко
- будете
- Уилсон
- в
- слова
- Работа
- работавший
- работает
- работает
- хуже
- лет
- Ты
- зефирнет
- нуль