Z umetno inteligenco so odkrili 'mrmranje' eliptične krivulje Take Flight | Revija Quanta

Eliptične krivulje so med bolj zapeljivimi predmeti v sodobni matematiki. Ne zdijo se zapleteni, vendar tvorijo hitro pot med matematiko, ki se je mnogi učijo v srednji šoli, in raziskovalno matematiko v njeni najbolj zapleteni obliki. Bili so osrednjega pomena za slavni dokaz Fermatovega zadnjega izreka Andrewa Wilesa v devetdesetih letih prejšnjega stoletja. So ključna orodja v sodobni kriptografiji. In leta 1990 je Clay Mathematics Institute imenoval a ugibanja o statistiki eliptičnih krivulj, enega od sedmih »nagradnih problemov tisočletja«, od katerih vsak nosi nagrado v višini 1 milijona dolarjev za svojo rešitev. To ugibanje, ki si ga je prvi upal Bryan Birch in Peter Swinnerton-Dyer v šestdesetih letih prejšnjega stoletja še vedno ni bilo dokazano.

Razumevanje eliptičnih krivulj je naporen podvig, ki je bil osrednjega pomena za matematiko. Tako je bil leta 2022, ko je čezatlantsko sodelovanje uporabilo statistične tehnike in umetno inteligenco za odkrivanje popolnoma nepričakovanih vzorcev v eliptičnih krivuljah, dobrodošel, čeprav nepričakovan, prispevek. »Bilo je le vprašanje časa, kdaj bo strojno učenje pristalo na našem pragu z nečim zanimivim,« je rekel Peter Sarnak, matematik na Inštitutu za napredne študije in univerzi Princeton. Sprva nihče ni mogel pojasniti, zakaj obstajajo na novo odkriti vzorci. Od takrat so matematiki v seriji nedavnih člankov začeli odkrivati ​​razloge za vzorce, ki so jih poimenovali "mrmranje" zaradi njihove podobnosti s tekočimi oblikami jat škorcev, in začeli dokazovati, da se ne smejo pojavljati samo v določenem primeri, pregledani leta 2022, vendar v eliptičnih krivuljah na splošno.

Kako pomembno je biti eliptičen

Da bi razumeli, kaj so ti vzorci, moramo postaviti temelje o tem, kaj so eliptične krivulje in kako jih matematiki kategorizirajo.

Eliptična krivulja povezuje kvadrat ene spremenljivke, običajno zapisano kot y, na tretjo potenco drugega, običajno zapisano kot x: y² = x³ + Ax + B, za nekaj parov številk A in B, Dokler A in B izpolnjevati nekaj enostavnih pogojev. Ta enačba določa krivuljo, ki jo je mogoče grafično prikazati na ravnini, kot je prikazano spodaj. (Kljub podobnosti v imenih elipsa ni eliptična krivulja.)

Čeprav so eliptične krivulje na videz preproste, se izkažejo za neverjetno zmogljiva orodja za teoretike števil – matematike, ki iščejo vzorce v celih številih. Namesto da bi prepustili spremenljivkam x in y razpon čez vsa števila, jih matematiki radi omejijo na različne številske sisteme, čemur pravijo definiranje krivulje "nad" danim številskim sistemom. Še posebej uporabne so eliptične krivulje, omejene na racionalna števila – števila, ki jih je mogoče zapisati kot ulomke. "Eliptične krivulje nad realnimi ali kompleksnimi številkami so precej dolgočasne," je dejal Sarnak. "Samo racionalna števila so globoka."

Tukaj je en način, ki je resničen. Če narišete ravno črto med dvema racionalnima točkama na eliptični krivulji, bo tudi mesto, kjer ta črta ponovno seka krivuljo, racionalno. To dejstvo lahko uporabite za definiranje "seštevanja" v eliptični krivulji, kot je prikazano spodaj.

Narišite črto med P in Q. Ta črta bo sekala krivuljo v tretji točki, R. (Matematiki imajo poseben trik za obravnavo primera, ko premica ne seka krivulje z dodajanjem »točke v neskončnosti«.) Odsev R čez x-os je vaša vsota P + Q. Skupaj s to operacijo seštevanja vse rešitve krivulje tvorijo matematični objekt, imenovan skupina.

Matematiki to uporabljajo za definiranje "ranga" krivulje. The rang krivulje se nanaša na število racionalnih rešitev, ki jih ima. Krivulje ranga 0 imajo končno število rešitev. Krivulje z višjim rangom imajo neskončno število rešitev, katerih razmerje med seboj z uporabo operacije dodajanja je opisano z rangom.

Uvrstitve niso dobro razumljene; matematiki nimajo vedno načina, kako bi jih izračunali in ne vedo, kako veliki lahko postanejo. (Največji točen rang, znan za določeno krivuljo, je 20.) Podobne krivulje imajo lahko popolnoma različne range.

Eliptične krivulje imajo veliko opraviti tudi s praštevili, ki so deljiva le z 1 in sama s seboj. Še posebej matematiki gledajo krivulje nad končnimi polji - sistemi ciklične aritmetike, ki so definirani za vsako praštevilo. Končno polje je kot ura s številom ur, ki je enako praštevilu: če nadaljujete štetje navzgor, se števila začnejo znova. V končnem polju za 7 je na primer 5 plus 2 enako nič, 5 plus 3 pa 1.

Eliptična krivulja ima povezano zaporedje števil, imenovano a_p, ki se nanaša na število rešitev krivulje v končnem polju, ki ga definira praštevilo p. Manjši a_p pomeni več rešitev; večji a_p pomeni manj rešitev. Čeprav je rang težko izračunati, zaporedje a_p je veliko lažje.

Na podlagi številnih izračunov, opravljenih na enem od prvih računalnikov, sta Birch in Swinnerton-Dyer domnevala razmerje med rangom eliptične krivulje in zaporedjem a_p. Kdor lahko dokaže, da je imel prav, bo osvojil milijon dolarjev in matematično nesmrtnost.

Pojavi se vzorec presenečenja

Po začetku pandemije, Yang-Hui He, raziskovalka na londonskem inštitutu za matematične znanosti, se je odločila za nove izzive. Na fakulteti je študiral fiziko in doktoriral iz matematične fizike na tehnološkem inštitutu v Massachusettsu. Toda čedalje bolj ga je zanimala teorija števil in glede na vse večje zmogljivosti umetne inteligence je pomislil, da bi poskusil uporabiti AI kot orodje za iskanje nepričakovanih vzorcev v številih. (Bil je že uporabo strojnega učenja razvrstiti Calabi-Yau mnogoterosti, matematične strukture, ki se pogosto uporabljajo v teoriji strun.)

Avgusta 2020, ko se je pandemija poglabljala, ga je Univerza v Nottinghamu gostila na spletni pogovor. Bil je pesimističen glede svojega napredka in same možnosti uporabe strojnega učenja za odkrivanje nove matematike. »Njegova pripoved je bila, da je teorija števil težka, ker se stvari v teoriji števil ne moreš strojno naučiti,« je dejal Thomas Oliver, matematik z Univerze Westminster, ki je bil med občinstvom. Kot se spominja: »Ničesar nisem mogel najti, ker nisem bil strokovnjak. Sploh nisem uporabljal pravih stvari, da bi to pogledal.”

Oliver in Kyu-Hwan Lee, matematik na Univerzi v Connecticutu, je začel sodelovati s He. "Za to smo se odločili samo zato, da bi izvedeli, kaj je strojno učenje, namesto da bi resno preučevali matematiko," je dejal Oliver. "Ampak hitro smo ugotovili, da se lahko strojno naučite veliko stvari."

Oliver in Lee sta predlagala, naj uporabi svoje tehnike za pregled L-funkcije, neskončni nizi, tesno povezani z eliptičnimi krivuljami skozi zaporedje a_p. Uporabili bi lahko spletno podatkovno zbirko eliptičnih krivulj in z njimi povezanih L-funkcije, imenovane LMFDB za usposabljanje njihovih klasifikatorjev strojnega učenja. Takrat je baza podatkov imela nekaj več kot 3 milijone eliptičnih krivulj nad racionalnimi vrednostmi. Do oktobra 2020 so imeli papir ki je uporabil informacije, pridobljene iz L-funkcije za napovedovanje določene lastnosti eliptičnih krivulj. Novembra so si delili drug papir ki je uporabil strojno učenje za razvrščanje drugih objektov v teoriji števil. Do decembra jim je uspelo napovedati range eliptičnih krivulj z visoko natančnostjo.

Vendar niso bili prepričani, zakaj njihovi algoritmi za strojno učenje delujejo tako dobro. Lee je prosil svojega dodiplomskega študenta Alekseja Pozdnjakova, da bi ugotovil, kaj se dogaja. Kot se zgodi, LMFDB razvrsti eliptične krivulje glede na količino, imenovano prevodnik, ki povzema informacije o praštevilih, pri katerih se krivulja ne obnaša dobro. Tako je Pozdnjakov poskušal hkrati opazovati veliko število krivulj s podobnimi vodniki - recimo vse krivulje z vodniki med 7,500 in 10,000.

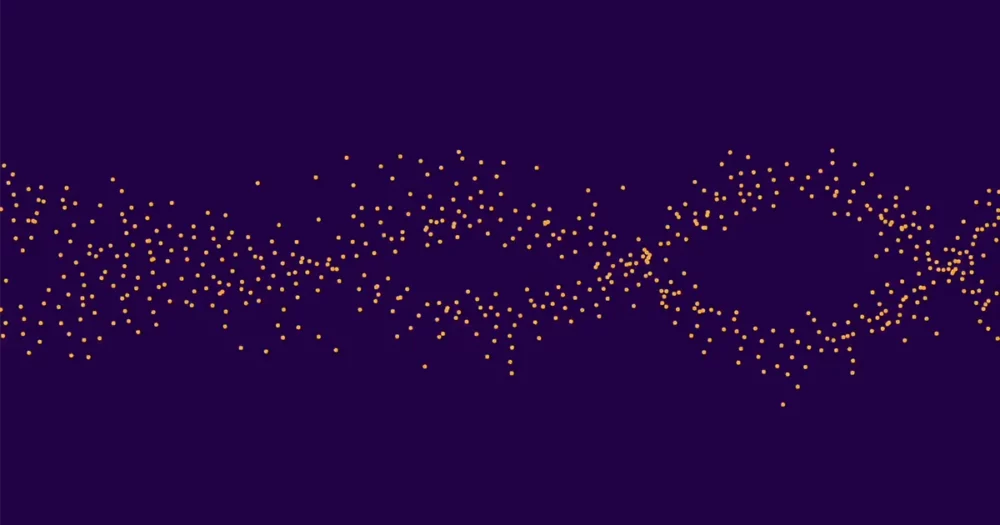
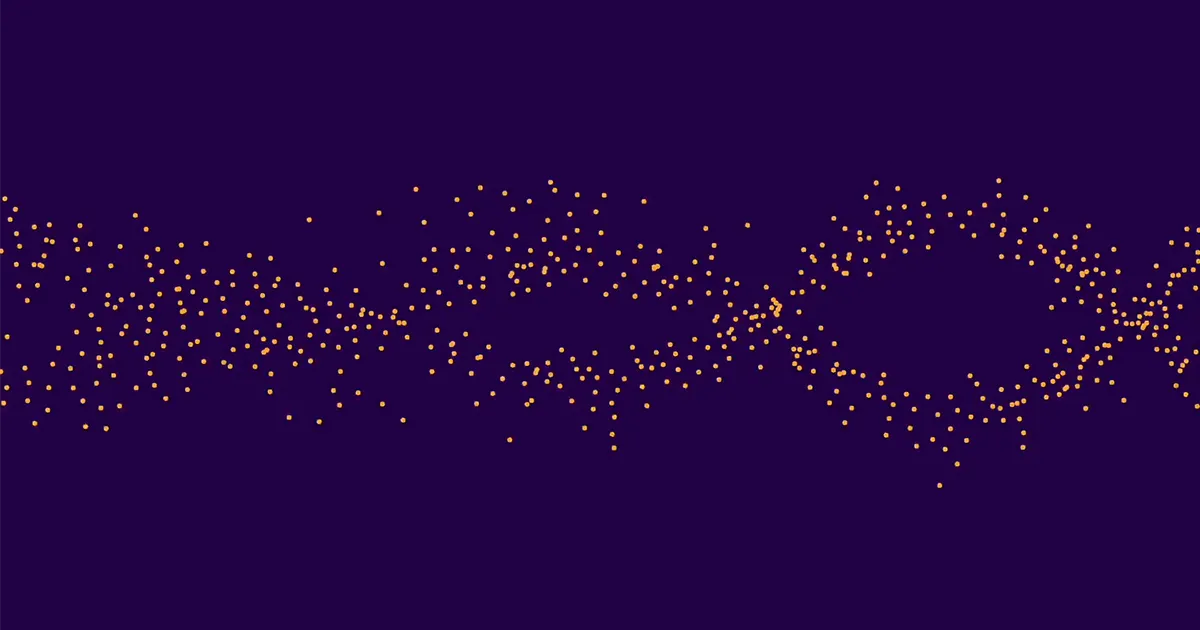
To je skupaj znašalo približno 10,000 krivulj. Približno polovica teh je imela rang 0 in polovica rang 1. (Višji rangi so izredno redki.) Nato je povprečil vrednosti a_p za vse krivulje ranga 0, ločeno povprečno a_p za vse krivulje ranga 1 in narisal rezultate. Dva niza pik sta tvorila dva različna, zlahka opazna vala. Zato so klasifikatorji strojnega učenja lahko pravilno ugotovili range določenih krivulj.

»Najprej sem bil le vesel, da sem opravil nalogo,« je dejal Pozdnjakov. "Toda Kyu-Hwan je takoj ugotovil, da je ta vzorec presenetljiv, in takrat je postal res razburljiv."

Lee in Oliver sta bila navdušena. "Alexey nam je pokazal sliko in rekel sem, da izgleda kot tisto, kar počnejo ptice," je dejal Oliver. "In potem je Kyu-Hwan to pogledal in rekel, da se imenuje mrmranje, nato pa je Yang rekel, da bi morali poklicati časopis"Mrmranje eliptičnih krivulj. ""

Svoj članek so naložili aprila 2022 in ga posredovali peščici drugih matematikov, ki so živčno pričakovali, da jim bodo povedali, da je njihovo tako imenovano "odkritje" dobro znano. Oliver je dejal, da je odnos tako viden, da bi ga morali opaziti že zdavnaj.

Prednatis je skoraj takoj vzbudil zanimanje, zlasti pri Andrew Sutherland, raziskovalec na MIT, ki je eden od odgovornih urednikov LMFDB. Sutherland je ugotovil, da 3 milijoni eliptičnih krivulj niso dovolj za njegove namene. Želel je pogledati veliko večje razpone prevodnikov, da bi ugotovil, kako robustni so bili šumi. Podatke je črpal iz drugega ogromnega skladišča približno 150 milijonov eliptičnih krivulj. Še vedno nezadovoljen je nato potegnil podatke iz drugega skladišča s 300 milijoni krivulj.

"Toda tudi to ni bilo dovolj, zato sem dejansko izračunal nov nabor podatkov z več kot milijardo eliptičnih krivulj in to je tisto, kar sem uporabil za izračun slik res visoke ločljivosti," je dejal Sutherland. Mrmranje se je pokazalo, ali je v povprečju izračunal več kot 15,000 eliptičnih krivulj naenkrat ali milijon naenkrat. Oblika je ostala enaka, tudi ko je gledal krivulje čez vedno večja praštevila, pojav, imenovan invariantnost lestvice. Sutherland je tudi ugotovil, da šumenje ni edinstveno za eliptične krivulje, ampak se pojavlja tudi v splošnejših L-funkcije. On je pisal pismo, ki povzema njegove ugotovitve in ga poslal Sarnaku in Michael Rubinstein na Univerzi Waterloo.

"Če obstaja znana razlaga za to, pričakujem, da jo boste vedeli," je zapisal Sutherland.

Niso.

Razlaga vzorca

Lee, He in Oliver so avgusta 2023 organizirali delavnico o mrmranju na Inštitutu za računalniške in eksperimentalne raziskave v matematiki (ICERM) Univerze Brown. Prišla sta Sarnak in Rubinstein, prav tako Sarnakov študent Nina Zubrilina.

Zubrilina je predstavila svoje raziskave vzorcev mrmranja v modularne oblike, posebne kompleksne funkcije, ki so kot eliptične krivulje povezane L-funkcije. V modularnih oblikah z velikimi prevodniki se šumi stekajo v ostro definirano krivuljo, namesto da tvorijo opazen, a razpršen vzorec. noter papir objavljeno 11. oktobra 2023, je Zubrilina dokazala, da ta vrsta mrmranja sledi eksplicitni formuli, ki jo je odkrila.

»Ninin velik dosežek je, da je dala formulo za to; Jaz temu pravim Zubrilina formula gostote šumenja,« je dejal Sarnak. "Z uporabo zelo sofisticirane matematike je dokazala natančno formulo, ki se popolnoma prilega podatkom."

Njena formula je zapletena, vendar jo Sarnak pozdravlja kot pomembno novo vrsto funkcije, primerljivo z Airyjevimi funkcijami, ki definirajo rešitve diferencialnih enačb, ki se uporabljajo v različnih kontekstih fizike, od optike do kvantne mehanike.

Čeprav je bila Zubrilinina formula prva, so ji sledile druge. "Zdaj vsak teden izide nov dokument," je dejal Sarnak, "v glavnem z uporabo Zubrilininih orodij, ki razlaga druge vidike mrmranja."

Jonathan Bober, Andrew Booker in Min lee Univerze v Bristolu, skupaj z David Lowry-Duda ICERM, je dokazal obstoj drugačne vrste mrmranja v modularnih oblikah v še en oktobrski časopis. In Kyu-Hwan Lee, Oliver in Pozdnyakov dokazal obstoj šumenja v predmetih, imenovanih Dirichletovi znaki, ki so tesno povezani z L-funkcije.

Sutherland je bil navdušen nad precejšnjo dozo sreče, ki je pripeljala do odkritja mrmranja. Če podatkov o eliptični krivulji ne bi naročil prevodnik, bi šumenje izginilo. "Imeli so srečo, da so jemali podatke iz LMFDB, ki so bili vnaprej razvrščeni glede na dirigenta," je dejal. »To je tisto, kar povezuje eliptično krivuljo z ustrezno modularno obliko, vendar to sploh ni očitno. ... Dve krivulji, katerih enačbe so zelo podobne, imata lahko zelo različne prevodnike.« Na primer, Sutherland je to opozoril y² = x³ - 11x + 6 ima vodnik 17, vendar če znak minus obrnemo na znak plus, y² = x³ + 11x + 6 ima vodnik 100,736.

Tudi tedaj so šumenje našli le zaradi neizkušenosti Pozdnjakova. »Mislim, da ga brez njega ne bi našli,« je dejal Oliver, »ker strokovnjaki tradicionalno normalizirajo a_p imeti absolutno vrednost 1. Vendar jih ni normaliziral … zato so bila nihanja zelo velika in vidna.«

Statistični vzorci, ki jih algoritmi umetne inteligence uporabljajo za razvrščanje eliptičnih krivulj po rangu, obstajajo v prostoru parametrov s stotinami dimenzij – preveč, da bi jih ljudje lahko razvrstili v svojih glavah, kaj šele vizualizirali, je opozoril Oliver. Toda čeprav je strojno učenje odkrilo skrita nihanja, "smo šele pozneje razumeli, da so to šumenje."

Opomba urednika: Andrew Sutherland, Kyu-Hwan Lee in zbirka podatkov L-funkcij in modularnih obrazcev (LMFDB) so vsi prejeli sredstva od fundacije Simons, ki financira tudi to uredniško neodvisno publikacijo. Odločitve o financiranju fundacije Simons nimajo vpliva na našo pokritost. Več informacij je na voljo tukaj.