1Instituut-Lorentz, Universiteit Leiden, 2300 RA Leiden, Nederländerna
2QuTech, Delft University of Technology, PO Box 5046, 2600 GA Delft, Nederländerna och JARA Institute for Quantum Information, Forschungszentrum Juelich, D-52425 Juelich, Tyskland
3Google Quantum AI, 80636 München, Tyskland
Hitta det här uppsatsen intressant eller vill diskutera? Scite eller lämna en kommentar på SciRate.
Abstrakt
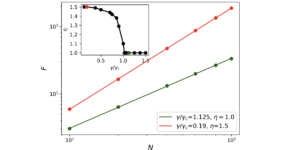
Kvantfasuppskattning är en hörnsten i design av kvantalgoritmer, vilket möjliggör slutledning av egenvärden för exponentiellt stora glesa matriser. Den maximala hastigheten med vilken dessa egenvärden kan läras in, – känd som Heisenberg-gränsen – är begränsad av gränser på kretsen komplexitet som krävs för att simulera en godtycklig Hamiltonian. Enkelkontrollerade qubit-varianter av kvantfasuppskattning som inte kräver koherens mellan experiment har fått intresse under de senaste åren på grund av lägre kretsdjup och minimal qubit-overhead. I detta arbete visar vi att dessa metoder kan uppnå Heisenberg-gränsen, $also$ när man inte kan förbereda systemets egentillstånd. Givet en kvantsubrutin som ger prov på en `fasfunktion' $g(k)=sum_j A_j e^{i phi_j k}$ med okända egenfaser $phi_j$ och överlappar $A_j$ vid kvantkostnad $O(k)$, vi visar hur man uppskattar faserna ${phi_j}$ med (root-mean-square) fel $delta$ för total kvantkostnad $T=O(delta^{-1})$. Vårt schema kombinerar idén med Heisenberg-begränsad flerordnings kvantfasuppskattning för en enda egenvärdesfas [Higgins et al (2009) och Kimmel et al (2015)] med subrutiner med så kallad tät kvantfasuppskattning som använder klassisk bearbetning via tidsserieanalys för QEEP-problemet [Somma (2019)] eller matrispennametoden. För vår algoritm som adaptivt fixar valet för $k$ i $g(k)$ bevisar vi Heisenberg-begränsad skalning när vi använder subrutinen tidsserie/QEEP. Vi presenterar numeriska bevis för att med hjälp av matrispenntekniken kan algoritmen också uppnå Heisenberg-begränsad skalning.
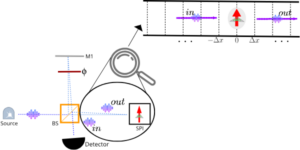
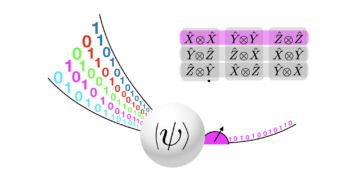
Utvald bild: Ett Heisenberg-begränsat schema för att detektera flera faser $phi_j$. Först görs en initial uppskattning av $phi_jin[0,2pi]$ från en tidsserie ${langle Urangle, langle U^2rangle ldots}$. Sedan görs en uppskattning av $kphi_j$ för några $k>1$, med hjälp av ${langle U^{k}rangle, langle U^{2k}rangle,ldots }$. Detta genererar en mer exakt uppskattning av $phi_j$ (mindre felstaplar), men modulo $2pi/k$. Data från den första uppskattningen används för att stabilisera denna uppskattning och ta bort oönskade alias (streckade linjer). Detta upprepas för allt större värden på $k$ för att uppnå Heisenberg-gränsen. Multiplikatorn $k$ väljs baserat på tidigare uppskattningar för att möjliggöra entydig uppskattning.
Populär sammanfattning
► BibTeX-data
► Referenser
[1] BL Higgins, DW Berry, SD Bartlett, MW Mitchell, HM Wiseman och GJ Pryde. Visar Heisenberg-begränsad entydig fasuppskattning utan adaptiva mätningar. New J. Phys., 11 (7): 073023, 2009. 10.1088/1367-2630/11/7/073023. URL https:///arxiv.org/abs/0809.3308.
https://doi.org/10.1088/1367-2630/11/7/073023
arXiv: 0809.3308
[2] Shelby Kimmel, Guang Hao Low och Theodore J. Yoder. Robust kalibrering av en universell en-qubit-gate-set via robust fasuppskattning. Phys. Rev. A, 92: 062315, 2015. 10.1103/PhysRevA.92.062315. URL https:///arxiv.org/abs/1502.02677.
https: / / doi.org/ 10.1103 / PhysRevA.92.062315
arXiv: 1502.02677
[3] Rolando D. Somma. Kvantegenvärdesuppskattning via tidsserieanalys. New J. Phys., 21: 123025, 2019. 10.1088/1367-2630/ab5c60. URL https:///iopscience.iop.org/article/10.1088/1367-2630/ab5c60/pdf.
https://doi.org/10.1088/1367-2630/ab5c60
[4] Pawel Wocjan och Shengyu Zhang. Flera naturliga BQP-kompletta problem. ArXiv:quant-ph/0606179, 2006. 10.48550/arXiv.quant-ph/0606179. URL https:///arxiv.org/abs/quant-ph/0606179.
https:///doi.org/10.48550/arXiv.quant-ph/0606179
arXiv: kvant-ph / 0606179
[5] Peter W. Shor. Polynom-tidsalgoritmer för primtalsfaktorisering och diskreta logaritmer på en kvantdator. SIAM J. Sci. Statistik. Comp., 26: 1484, 1997. 10.1137/S0097539795293172. URL https:///arxiv.org/abs/quant-ph/9508027.
https: / / doi.org/ 10.1137 / S0097539795293172
arXiv: kvant-ph / 9508027
[6] Aram W. Harrow, Avinatan Hassidim och Seth Lloyd. Kvantalgoritm för att lösa linjära ekvationssystem. Phys. Rev. Lett., 15 (103): 150502, 2009. 10.1103/PhysRevLett.103.150502. URL https:///arxiv.org/abs/0811.3171.
https: / / doi.org/ 10.1103 / PhysRevLett.103.150502
arXiv: 0811.3171
[7] James D. Whitfield, Jacob Biamonte och Alán Aspuru-Guzik. Simulering av elektronisk struktur Hamiltonians med hjälp av kvantdatorer. Mol. Phys., 109: 735–750, 2011. 10.1080/00268976.2011.552441. URL https:///arxiv.org/abs/1001.3855.
https: / / doi.org/ 10.1080 / 00268976.2011.552441
arXiv: 1001.3855
[8] MA Nielsen och IL Chuang. Kvantberäkning och kvantinformation. Cambridge-serien om information och naturvetenskap. Cambridge University Press, 2000. ISBN 9780521635035. 10.1017/CBO9780511976667. URL https:///books.google.de/books?id=65FqEKQOfP8C.
https: / / doi.org/ 10.1017 / CBO9780511976667
https:///books.google.de/books?id=65FqEKQOfP8C
[9] R. Cleve, A. Ekert, C. Macchiavello och M. Mosca. Kvantalgoritmer återbesöks. Proceedings of the Royal Society of London. Serie A: Mathematical, Physical and Engineering Sciences, 454 (1969): 339–354, 1998. 10.1098/rspa.1998.0164. URL https://royalsocietypublishing.org/doi/abs/10.1098/rspa.1998.0164.
https: / / doi.org/ 10.1098 / rspa.1998.0164
[10] Vittorio Giovannetti, Seth Lloyd och Lorenzo Maccone. Kvantmetrologi. Physical review letters, 96 (1): 010401, 2006. 10.1103/PhysRevLett.96.010401. URL https:///journals.aps.org/prl/abstract/10.1103/PhysRevLett.96.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.96.010401
[11] Wim van Dam, G. Mauro D'Ariano, Artur Ekert, Chiara Macchiavello och Michele Mosca. Optimala kvantkretsar för allmän fasuppskattning. Phys. Rev. Lett., 98: 090501, Mar 2007. 10.1103/PhysRevLett.98.090501. URL https:///link.aps.org/doi/10.1103/PhysRevLett.98.090501.
https: / / doi.org/ 10.1103 / PhysRevLett.98.090501
[12] Dominic W Berry, Brendon L Higgins, Stephen D Bartlett, Morgan W Mitchell, Geoff J Pryde och Howard M Wiseman. Hur man utför så exakta möjliga fasmätningar. Physical Review A, 80 (5): 052114, 2009. 10.1103/PhysRevA.80.052114.
https: / / doi.org/ 10.1103 / PhysRevA.80.052114
[13] Robert B. Griffiths och Chi-Sheng Niu. Semiklassisk Fouriertransform för kvantberäkning. Physical Review Letters, 76 (17): 3228–3231, apr 1996. ISSN 1079-7114. 10.1103/physrevlett.76.3228. URL 10.1103/PhysRevLett.76.3228.
https: / / doi.org/ 10.1103 / physrevlett.76.3228
http:///10.1103/PhysRevLett.76.3228
[14] A. Yu. Kitaev. Kvantmätningar och det abelska stabilisatorproblemet. ArXiv:quant-ph/9511026, 1995. 10.48550/arXiv.quant-ph/9511026. URL https:///arxiv.org/abs/quant-ph/9511026.
https:///doi.org/10.48550/arXiv.quant-ph/9511026
arXiv: kvant-ph / 9511026
[15] Dominic W. Berry, Graeme Ahokas, Richard Cleve och Barry C. Sanders. Effektiva kvantalgoritmer för att simulera glesa Hamiltonianer. Comm. Matematik. Phys., 270 (359), 2007. 10.1007/s00220-006-0150-x. URL https:///arxiv.org/abs/quant-ph/0508139.
https: / / doi.org/ 10.1007 / s00220-006-0150-x
arXiv: kvant-ph / 0508139
[16] Nathan Wiebe och Chris Granade. Effektiv Bayesiansk fasuppskattning. Phys. Rev. Lett., 117: 010503, 2016. 10.1103/PhysRevLett.117.010503. URL https:///arxiv.org/abs/1508.00869.
https: / / doi.org/ 10.1103 / PhysRevLett.117.010503
arXiv: 1508.00869
[17] Krysta M. Svore, Matthew B. Hastings och Michael Freedman. Snabbare fasuppskattning. Kvant. Inf. Comp., 14 (3-4): 306–328, 2013. 10.48550/arXiv.1304.0741. URL https:///arxiv.org/abs/1304.0741.
https:///doi.org/10.48550/arXiv.1304.0741
arXiv: 1304.0741
[18] Ewout van den Berg. Effektiv Bayesiansk fasuppskattning med hjälp av blandade priors. ArXiv:2007.11629, 2020. 10.22331/q-2021-06-07-469. URL https:///arxiv.org/abs/2007.11629.
https://doi.org/10.22331/q-2021-06-07-469
arXiv: 2007.11629
[19] Thomas E O'Brien, Brian Tarasinski och Barbara M Terhal. Kvantfasuppskattning av multipla egenvärden för småskaliga (brusiga) experiment. New J. Phys., 21: 023022, 2019. 10.1088/1367-2630/aafb8e. URL https://iopscience.iop.org/article/10.1088/1367-2630/aafb8e.
https: / / doi.org/ 10.1088 / 1367-2630 / aafb8e
[20] David C. Rife och Robert R. Boorstyn. Entonsparameteruppskattning från diskreta tidsobservationer. IEEE Trans. Inf. Th., 20 (5): 591–598, 1974. 10.1109/TIT.1974.1055282. URL https:///ieeexplore.ieee.org/document/1055282.
https: / / doi.org/ 10.1109 / TIT.1974.1055282
https: / / ieeexplore.ieee.org/ dokument / 1055282
[21] Sirui Lu, Mari Carmen Bañuls och J. Ignacio Cirac. Algoritmer för kvantsimulering vid ändliga energier. PRX Quantum, 2: 020321, 2020. 10.1103/PRXQuantum.2.020321. URL https:///journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.2.020321.
https: / / doi.org/ 10.1103 / PRXQuantum.2.020321
[22] TE O'Brien, S. Polla, NC Rubin, WJ Huggins, S. McArdle, S. Boixo, JR McClean och R. Babbush. Felavhjälpning via verifierad fasuppskattning. ArXiv:2010.02538, 2020. 10.1103/PRXQuantum.2.020317. URL https:///arxiv.org/abs/2010.02538.
https: / / doi.org/ 10.1103 / PRXQuantum.2.020317
arXiv: 2010.02538
[23] Alessandro Roggero. Spektraldensitetsuppskattning med den Gaussiska integraltransformen. ArXiv:2004.04889, 2020. 10.1103/PhysRevA.102.022409. URL https://arxiv.org/abs/2004.04889.
https: / / doi.org/ 10.1103 / PhysRevA.102.022409
arXiv: 2004.04889
[24] András Gilyén, Yuan Su, Guang Hao Low och Nathan Wiebe. Kvantsingular värdetransformation och bortom: Exponentiella förbättringar för kvantmatrisaritmetik. In Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing, STOC 2019, sid 193–204, New York, NY, USA, 2019. Association for Computing Machinery. ISBN 9781450367059. 10.1145/3313276.3316366. URL 10.1145/3313276.3316366.
https: / / doi.org/ 10.1145 / 3313276.3316366
[25] O. Regev. En subexponentiell tidsalgoritm för det dihedriska dolda undergruppsproblemet med polynomutrymme. ArXiv:quant-ph/0406151, 2004. 10.48550/arXiv.quant-ph/0406151. URL https:///arxiv.org/abs/quant-ph/0406151.
https:///doi.org/10.48550/arXiv.quant-ph/0406151
arXiv: kvant-ph / 0406151
[26] Lin Lin och Yu Tong. Heisenberg-begränsad marktillståndsenergiuppskattning för tidiga feltoleranta kvantdatorer. ArXiv:2102.11340, 2021. 10.1103/PRXQuantum.3.010318. URL https:///arxiv.org/abs/2102.11340.
https: / / doi.org/ 10.1103 / PRXQuantum.3.010318
arXiv: 2102.11340
[27] Valentin Gebhart, Augusto Smerzi och Luca Pezzè. Heisenberg-begränsad bayesisk flerfasuppskattningsalgoritm. ArXiv:2010.09075, 2020. 10.1103/PhysRevApplied.16.014035. URL https:///arxiv.org/abs/2010.09075.
https: / / doi.org/ 10.1103 / PhysRevApplied.16.014035
arXiv: 2010.09075
[28] Andrew M. Childs, Yuan Su, Minh C. Tran, Nathan Wiebe och Shuchen Zhu. Teori om travfel med kommutatorskalning. Phys. Rev. X, 11: 011020, februari 2021. 10.1103/PhysRevX.11.011020. URL https:///link.aps.org/doi/10.1103/PhysRevX.11.011020.
https: / / doi.org/ 10.1103 / PhysRevX.11.011020
[29] Harald Cramér. Matematiska metoder för statistik. Princeton University Press, 1946. ISBN 0691080046. 10.1515/9781400883868. URL https:///archive.org/details/in.ernet.dli.2015.223699.
https: / / doi.org/ 10.1515 / 9781400883868
https:///archive.org/details/in.ernet.dli.2015.223699
[30] Calyampudi Radakrishna Rao. Information och den noggrannhet som kan uppnås vid uppskattning av statistiska parametrar. Tjur. Calcutta matematik. Soc., 37: 81–89, 1945. 10.1007/978-1-4612-0919-5_16. URL https:///link.springer.com/chapter/10.1007/978-1-4612-0919-5_16.
https://doi.org/10.1007/978-1-4612-0919-5_16
[31] Yingbo Hua och Tapan Sarkar. Matrispennametod för att uppskatta parametrar för exponentiellt dämpade/odämpade sinusoider i brus. IEEE Transactions on Acoustic Speech and Signal Processing, 38 (5), 1990. 10.1109/29.56027. URL https:///ieeexplore.ieee.org/document/56027.
https: / / doi.org/ 10.1109 / 29.56027
https: / / ieeexplore.ieee.org/ dokument / 56027
[32] Ankur Moitra. Superupplösning, extrema funktioner och villkorsnumret för Vandermonde-matriser. I Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, STOC '15, sid 821–830, New York, NY, USA, 2015. Association for Computing Machinery. ISBN 9781450335362. 10.1145/2746539.2746561. URL 10.1145/2746539.2746561.
https: / / doi.org/ 10.1145 / 2746539.2746561
[33] Lin Lin och Yu Tong. Nästan optimal marktillståndsberedning. Quantum, 4: 372, december 2020. ISSN 2521-327X. 10.22331/q-2020-12-14-372. Webbadress 10.22331/q-2020-12-14-372.
https://doi.org/10.22331/q-2020-12-14-372
Citerad av
[1] Casper Gyurik, Chris Cade och Vedran Dunjko, "Mot kvantfördelar via topologisk dataanalys", arXiv: 2005.02607.
[2] Kianna Wan, Mario Berta och Earl T. Campbell, "Randomized Quantum Algorithm for Statistical Phase Estimation", Fysiska granskningsbrev 129 3, 030503 (2022).
[3] Andrés Gómez och Javier Mas, "Hermitisk matrisdefinititet från kvantfasuppskattning", Kvantinformationsbehandling 21 6, 213 (2022).
Ovanstående citat är från SAO / NASA ADS (senast uppdaterad framgångsrikt 2022-10-07 02:35:12). Listan kan vara ofullständig eftersom inte alla utgivare tillhandahåller lämpliga och fullständiga citatdata.
Det gick inte att hämta Crossref citerade data under senaste försöket 2022-10-07 02:35:10: Det gick inte att hämta citerade data för 10.22331 / q-2022-10-06-830 från Crossref. Detta är normalt om DOI registrerades nyligen.
Detta papper publiceras i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) licens. Upphovsrätten kvarstår med de ursprungliga upphovsrättsinnehavarna som författarna eller deras institutioner.