Matematiker slår tärning och skaffar sten-pappersax

När Bill Gates berättar historien utmanade Warren Buffett honom en gång till ett tärningsspel. Var och en skulle välja en av fyra tärningar som tillhörde Buffett, och sedan kastade de, med det högre numret som vann. Dessa var inte standardtärningar – de hade ett annat sortiment av nummer än de vanliga 1 till 6. Buffett erbjöd sig att låta Gates välja först, så att han kunde välja den starkaste tärningen. Men efter att Gates undersökt tärningarna, returnerade han ett motförslag: Buffett borde välja först.

Gates hade insett att Buffetts tärningar uppvisade en märklig egenskap: Ingen av dem var den starkaste. Om Gates hade valt först, vilken tärning han än valde, skulle Buffett ha kunnat hitta en annan tärning som kunde slå den (det vill säga en med mer än 50 % chans att vinna).

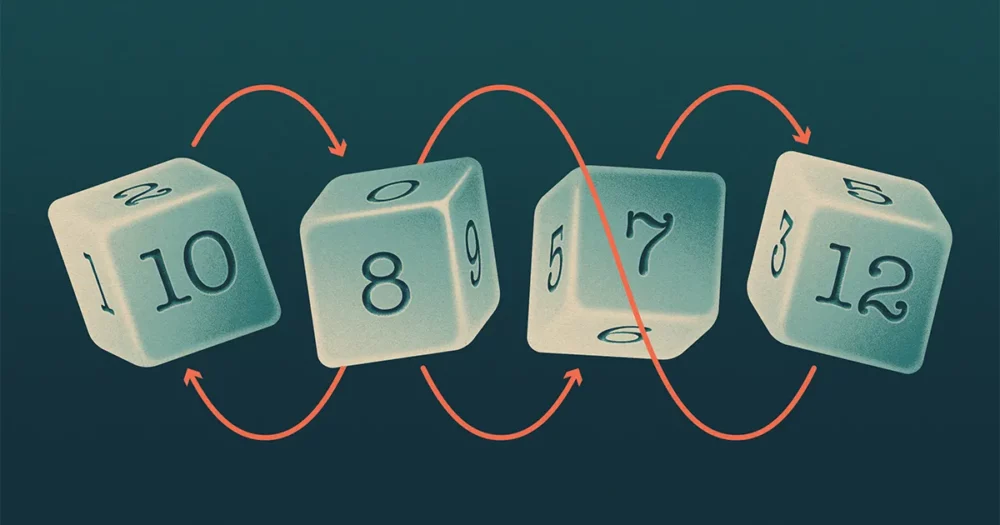
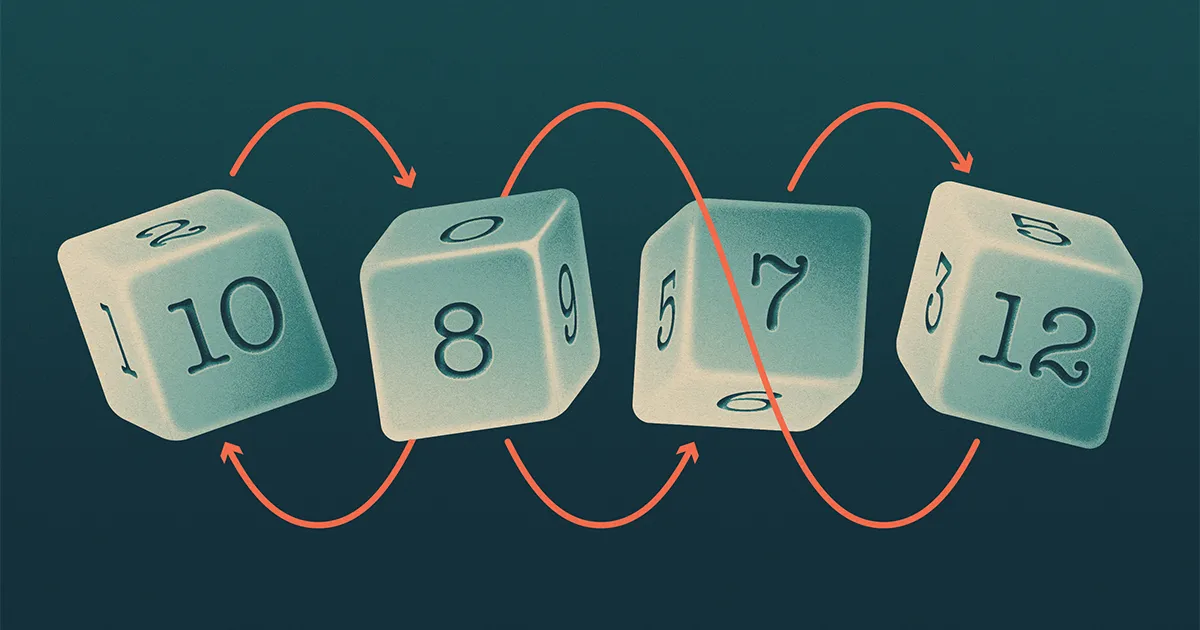
Buffetts fyra tärningar (kalla dem A, B, C och D) bildade ett mönster, som påminner om sten-pappers-sax, i vilket A beats B, B beats C, C beats D och D beats A. Matematiker säger att en sådan uppsättning tärningar är "otransitiv".

"Det är inte intuitivt alls att [intransitiv tärning] ens borde existera," sa Brian Conrey, chef för American Institute of Mathematics (AIM) i San Jose, som skrev en inflytelserik artikel om ämnet 2013.

Matematiker kom på första exemplen av intransitiv tärning för mer än 50 år sedan, och så småningom visat att när du överväger tärningar med fler och fler sidor, är det möjligt att skapa intransitiva cykler av vilken längd som helst. Vad matematiker inte visste förrän nyligen var hur vanliga intransitiva tärningar är. Måste du skapa sådana exempel noggrant, eller kan du välja tärningar slumpmässigt och ha en bra chans att hitta en intransitiv uppsättning?

Tittar på tre tärningar, om du vet det A beats B och B beats C, det verkar vara bevis på det A är den starkaste; situationer där C beats A borde vara sällsynt. Och faktiskt, om siffrorna på tärningarna tillåts summera till olika summor, så tror matematiker att denna intuition stämmer.

Men a papper som läggs ut på nätet slutet av förra året visar att i en annan naturlig miljö misslyckas denna intuition spektakulärt. Anta att du kräver att dina tärningar endast använder de nummer som visas på en vanlig tärning och har samma summa som en vanlig tärning. Då visade tidningen om A beats B och B beats C, A och C har i stort sett lika chanser att vinna mot varandra.

"Veta att A beats B och B beats C ger dig bara ingen information om huruvida A beats C, "Sade Timothy Gowers från University of Cambridge, en Fields-medaljör och en av bidragsgivarna till det nya resultatet, vilket bevisades genom ett öppet onlinesamarbete känt som ett Polymath-projekt.

Under tiden en annan nyligen papper analyserar set med fyra eller fler tärningar. Det fyndet är utan tvekan ännu mer paradoxalt: om du till exempel väljer fyra tärningar slumpmässigt och du finner att A beats B, B beats C och C beats D, då är det lite mer sannolikt för D att slå A än tvärtom.

Varken stark eller svag

De senaste resultatutslagen började för ungefär ett decennium sedan, efter att Conrey deltog i en sammankomst för matematiklärare med en session som täckte intransitiva tärningar. "Jag hade ingen aning om att sådana saker kunde existera," sa han. "Jag blev lite fascinerad av dem."

Han bestämde sig (senare sällskap av sin kollega Kent Morrison på AIM) för att utforska ämnet med tre gymnasieelever som han var mentor – James Gabbard, Katie Grant och Andrew Liu. Hur ofta, undrade gruppen, kommer slumpmässigt valda tärningar att bilda en intransitiv cykel?

Intransitiva uppsättningar av tärningar anses vara sällsynta om tärningarnas ansiktsnummer summerar till olika summor, eftersom tärningen med den högsta summan sannolikt kommer att slå de andra. Så teamet bestämde sig för att fokusera på tärningar som har två egenskaper: För det första använder tärningarna samma nummer som på en standardtärning - 1 till och med n, i fallet med en n-sidig dö. Och för det andra, ansiktssiffrorna summerar till samma summa som på en standardtärning. Men till skillnad från standardtärningar kan varje tärning upprepa några av siffrorna och utelämna andra.

När det gäller sexsidiga tärningar finns det bara 32 olika tärningar som har dessa två egenskaper. Så med hjälp av en dator kunde teamet identifiera alla trippel där A beats B och B beats C. Det fann forskarna till sin förvåning A beats C i 1,756 XNUMX trippel och C beats A i 1,731 XNUMX trippel — nästan identiska tal. Baserat på denna beräkning och simuleringar av tärningar med mer än sex sidor, antog laget att när antalet sidor på tärningen närmar sig oändligheten, är sannolikheten att A beats C närmar sig 50 %.

Förmodan, med sin blandning av tillgänglighet och nyans, slog Conrey som ett bra foder för ett Polymath-projekt, där många matematiker samlas online för att dela idéer. I mitten av 2017 föreslog han idén till Gowers, upphovsmannen till Polymath-metoden. "Jag gillade frågan väldigt mycket på grund av dess överraskningsvärde," sa Gowers. Han skrev en blogginlägg om gissningarna som lockade till sig en uppsjö av kommentarer, och under loppet av sex ytterligare inlägg lyckades kommentatorerna bevisa det.

I deras papper, postat på nätet i slutet av november 2022 handlar en viktig del av beviset om att visa att det för det mesta inte är meningsfullt att prata om huruvida en enda tärning är stark eller svag. Buffetts tärningar, varav ingen är den starkaste i flocken, är inte så ovanliga: Om du väljer en tärning på måfå, visade Polymath-projektet, är det troligt att det slår ungefär hälften av de andra tärningarna och förlorar mot den andra halvan. "Nästan varje tärning är ganska genomsnittlig," sa Gowers.

Projektet avvek från AIM-teamets ursprungliga modell i ett avseende: För att förenkla vissa tekniska detaljer, förklarade projektet att ordningen på siffrorna på en tärning spelar roll - så till exempel 122556 och 152562 skulle betraktas som två olika tärningar. Men Polymath-resultatet, i kombination med AIM-teamets experimentella bevis, skapar en stark presumtion om att gissningen också är sann i den ursprungliga modellen, sa Gowers.

"Jag var väldigt glad över att de kom med detta bevis," sa Conrey.

När det kom till samlingar av fyra eller fler tärningar, hade AIM-teamet förutspått liknande beteende som tre tärningar: Till exempel, om A beats B, B beats C och C beats D då borde det finnas en ungefär 50-50 sannolikhet att D beats A, närmar sig exakt 50-50 när antalet sidor på tärningen närmar sig oändligheten.

För att testa gissningarna simulerade forskarna head-to-head-turneringar för set med fyra tärningar med 50, 100, 150 och 200 sidor. Simuleringarna följde inte deras förutsägelser lika noga som i fallet med tre tärningar men var fortfarande tillräckligt nära för att stärka deras tro på gissningarna. Men även om forskarna inte insåg det, bar dessa små avvikelser ett annat budskap: För uppsättningar av fyra eller fler tärningar är deras gissningar falska.

"Vi ville verkligen att [gissningarna] skulle vara sanna, för det skulle vara coolt," sa Conrey.

När det gäller fyra tärningar, Elisabetta Cornacchia av det schweiziska federala tekniska institutet Lausanne och Jan Hązła från African Institute for Mathematical Sciences i Kigali, Rwanda, visade i en papper publicerade online i slutet av 2020 att om A beats B, B beats C och C beats Doch sedan D har en något bättre än 50% chans att slå A — förmodligen någonstans runt 52 %, sa Hązła. (Som med Polymath-pappret använde Cornacchia och Hązła en något annorlunda modell än i AIM-pappret.)

Cornacchia och Hązłas upptäckt framgår av det faktum att även om som regel en enstaka tärning varken är stark eller svag, kan ett par tärningar ibland ha gemensamma styrkeområden. Om du väljer två tärningar slumpmässigt, visade Cornacchia och Hązła, det finns en hyfsad sannolikhet att tärningarna kommer att vara korrelerade: de tenderar att slå eller förlora mot samma tärning. "Om jag ber dig att skapa två tärningar som är nära varandra, visar det sig att detta är möjligt," sa Hązła. Dessa små fickor av korrelation knuffar turneringsresultat bort från symmetri så snart det finns minst fyra tärningar i bilden.

De senaste tidningarna är inte slutet på historien. Cornacchia och Hązłas tidning börjar bara avslöja exakt hur korrelationer mellan tärningar obalanserar turneringarnas symmetri. Men under tiden vet vi nu att det finns gott om uppsättningar av intransitiva tärningar där ute - kanske till och med en som är tillräckligt subtil för att lura Bill Gates att välja först.