The Gauge Picture of Quantum Dynamics

The Gauge Picture of Quantum Dynamics

Tidsstämpel: 21 mars 2024 6:43

Kevin Slagle

Institutionen för elektro- och datorteknik, Rice University, Houston, Texas 77005 USA
Institutionen för fysik, California Institute of Technology, Pasadena, Kalifornien 91125, USA
Institute for Quantum Information and Matter och Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, Kalifornien 91125, USA

Hitta det här uppsatsen intressant eller vill diskutera? Scite eller lämna en kommentar på SciRate.

Abstrakt

Även om lokala Hamiltonianer uppvisar lokal tidsdynamik är denna lokalitet inte explicit i Schrödingerbilden i den meningen att vågfunktionsamplituderna inte följer en lokal rörelseekvation. Vi visar att geometrisk lokalitet kan uppnås explicit i rörelseekvationerna genom att "mäta" kvantmekanikens globala enhetliga invarians till en lokal mätinvarians. Det vill säga, förväntningsvärden $langle psi|A|psi rangle$ är invarianta under en global enhetlig transformation som verkar på vågfunktionen $|psirangle till U |psirangle$ och operatorerna $A till UAU^dolk$, och vi visar att det är möjligt att mäta denna globala invarians till en lokal mätinvarians. För att göra detta ersätter vi vågfunktionen med en samling lokala vågfunktioner $|psi_Jrangle$, en för varje utrymme $J$. Samlingen av rumsliga lappar är vald för att täcka utrymmet; t.ex. kan vi välja att lapparna ska vara enstaka qubits eller närmaste grannplatser på ett gitter. Lokala vågfunktioner associerade med närliggande par av rumsliga patchar $I$ och $J$ är relaterade till varandra genom dynamiska enhetstransformationer $U_{IJ}$. De lokala vågfunktionerna är lokala i den meningen att deras dynamik är lokal. Det vill säga, rörelseekvationerna för de lokala vågfunktionerna $|psi_Jrangle$ och förbindelserna $U_{IJ}$ är explicit lokala i rymden och beror bara på närliggande Hamiltonska termer. (De lokala vågfunktionerna är vågfunktioner med många kroppar och har samma Hilbert-rymddimension som den vanliga vågfunktionen.) Vi kallar denna bild av kvantdynamik mätbilden eftersom den uppvisar en lokal mätinvarians. Den lokala dynamiken för en enda rumslig fläck är relaterad till interaktionsbilden, där interaktionen Hamiltonian består av endast närliggande Hamiltonian termer. Vi kan också generalisera den explicita lokaliteten till att inkludera lokalitet i lokal laddning och energitätheter.

The Gauge Picture of Quantum Dynamics PlatoBlockchain Data Intelligence. Vertikal sökning. Ai.

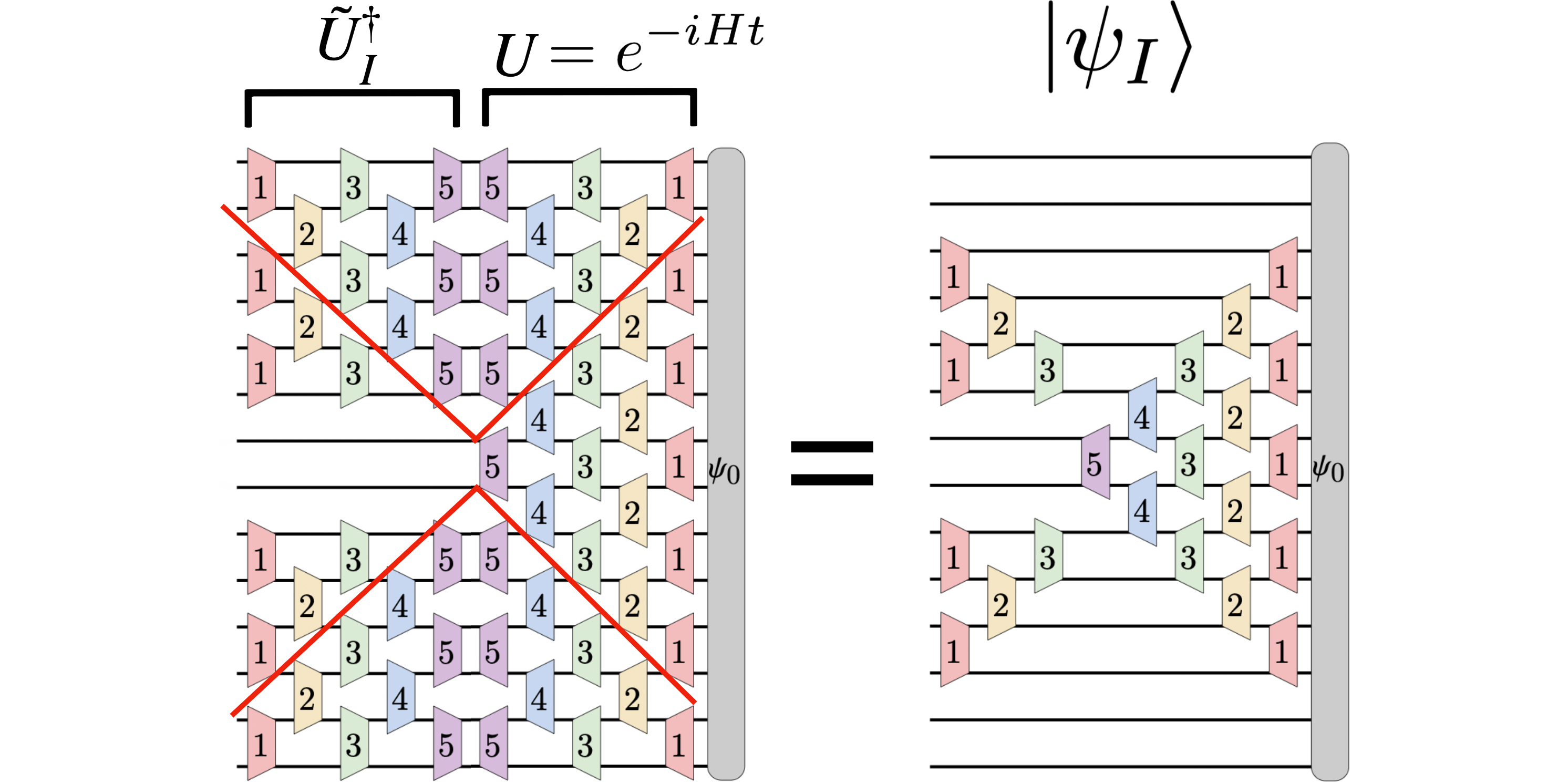
Utvald bild: I Schrodingers bild utvecklas en initial vågfunktion $|psi_0rangle$ till $U(t) |psi_0rangle$ efter en tid $t$, där $U(t) = e^{-iHt}$ är den enhetliga tidsutvecklingen operatör. Mätarbilden tar istället hänsyn till lokala vågfunktioner $|psi_I(t)rangle$ som är associerade med en delmängd (eller patch) $I$ i rymden. Den tidsutvecklade lokala vågfunktionen $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ erhålls från Schrodingers vågfunktion $|psi(t)rangle = U(t) |psi_0rangle $ via enhetsoperatorn $tilde{U}_I^dagger(t)$, som vänder tidsutvecklingen utanför regionen $I$. Som ett resultat beror den lokala vågfunktionsdynamiken $partial_I |psi_I(t)rangle$ endast på närliggande Hamiltonska termer som överlappar med regionen $I$. Figuren visar dessa enhetsoperatorer som kvantkretsar och visar att mycket av tiden evolutionen från $U(t)$ avbryts med $tilde{U}_I^dagger(t)$, vilket bara lämnar en timglasformad tidsevolutionsoperator som verkar på den initiala vågfunktionen (till höger i figuren). Denna timglasformade operatör är analog med den ljuskonformade operatörstillväxten i Heisenbergs bild.

Populär sammanfattning

De två mest kända bilderna av kvantdynamik är Schrodinger- och Heisenberg-bilderna. I Schrodingers bild utvecklas vågfunktionen i tiden, medan i Heisenbergs bild är vågfunktionen konstant men operatorerna utvecklas i tiden. I detta arbete introducerar vi en ny bild av kvantdynamik, mätarbilden, som gör djupa kopplingar till informationsort och mätteori.

Angående lokalitet: En trevlig fördel med Heisenbergs bild är att lokalitet är explicit i rörelseekvationerna. Det vill säga tidsutvecklingen för en lokal operatör beror endast på tillståndet för närliggande lokala operatörer. Däremot är lokalitet inte explicit på detta sätt i Schrodingers bild, för vilken det finns en enda vågfunktion vars tidsdynamik beror på operatörer överallt i rymden. Vår nya mätare bild modifierar Schrodingers bild så att vi kan beräkna en "lokal vågfunktion" som bär samma information som Schrodingers vågfunktion, förväntar oss att tidsdynamiken för lokala vågfunktioner i mätarbilden endast beror på närliggande Hamiltonska termer, vilket gör lokaliteten explicit i rörelseekvationer. För att uppnå denna explicita lokalitet lägger mätarbilden till mätfält till rörelseekvationerna.

Gauge-teori etablerar en djup koppling mellan en Hamiltonian (eller Lagrangian) med en global symmetri och en annan Hamiltonian där den globala symmetrin ersätts av en lokal mätarsymmetri via tilläggsdynamiska mätfält. Intressant nog medger Schrödingers ekvation $ihbar partial_t |psirangle = H |psirangle$ en global enhetlig invarians som ges av transformationen $|psirangle till U |psirangle$ och $H till UHU^dolk$. Vårt arbete visar att det också är möjligt att tillämpa gauge-teori på denna globala invarians i Schrodingers ekvation för att få en ny rörelseekvation, dvs. gauge-bilden, med dynamiska gauge-fält och en lokal gauge-invarians.

► BibTeX-data

► Referenser

[1] David Deutsch och Patrick Hayden. "Informationsflöde i intrasslade kvantsystem". Proceedings of the Royal Society of London Series A 456, 1759 (2000). arXiv:quant-ph/​9906007.
https: / / doi.org/ 10.1098 / rspa.2000.0585
arXiv: kvant-ph / 9906007

[2] Michael A. Levin och Xiao-Gang Wen. "String-net kondensation: En fysisk mekanism för topologiska faser". Phys. Rev. B 71, 045110 (2005). arXiv:cond-mat/​0404617.
https: / / doi.org/ 10.1103 / PhysRevB.71.045110
arXiv: cond-mat / 0404617

[3] T. Senthil, Ashvin Vishwanath, Leon Balents, Subir Sachdev och Matthew PA Fisher. "Avgränsade kvantkritiska poäng". Science 303, 1490–1494 (2004). arXiv:cond-mat/​0311326.
https: / / doi.org/ 10.1126 / science.1091806
arXiv: cond-mat / 0311326

[4] Beni Yoshida. "Exotisk topologisk ordning i fraktala spinnvätskor". Phys. Rev. B 88, 125122 (2013). arXiv:1302.6248.
https: / / doi.org/ 10.1103 / PhysRevB.88.125122
arXiv: 1302.6248

[5] Kevin Hartnett. "Matrix multiplikation tum närmare mytiska mål". Quanta Magazine (2021). URL: https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​.
https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​

[6] Volker Strassen. "Gaussisk eliminering är inte optimal". Numerische Mathematik 13, 354–356 (1969).
https: / / doi.org/ 10.1007 / BF02165411

[7] Kevin Slagle. "Quantum Gauge Networks: A New Kind of Tensor Network". Quantum 7, 1113 (2023). arXiv:2210.12151.
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
arXiv: 2210.12151

[8] Román Orús. "En praktisk introduktion till tensornätverk: Matrisprodukttillstånd och projicerade intrasslade partillstånd". Annals of Physics 349, 117–158 (2014). arXiv:1306.2164.
https: / / doi.org/ 10.1016 / j.aop.2014.06.013
arXiv: 1306.2164

[9] Michael P. Zaletel och Frank Pollmann. "Isometriska tensornätverkstillstånd i två dimensioner". Phys. Rev. Lett. 124, 037201 (2020). arXiv:1902.05100.
https: / / doi.org/ 10.1103 / PhysRevLett.124.037201
arXiv: 1902.05100

[10] Steven Weinberg. "Testa kvantmekanik". Annals of Physics 194, 336–386 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

[11] N. Gisin. "Weinbergs icke-linjära kvantmekanik och supraluminala kommunikationer". Physics Letters A 143, 1–2 (1990).
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

[12] Joseph Polchinski. "Weinbergs olinjära kvantmekanik och einstein-podolsky-rosen-paradoxen". Phys. Rev. Lett. 66, 397-400 (1991).
https: / / doi.org/ 10.1103 / PhysRevLett.66.397

[13] Kevin Slagle. "Testa kvantmekanik med bullriga kvantdatorer" (2021). arXiv:2108.02201.
arXiv: 2108.02201

[14] Brian Swingle. "Avkodning av fysiken för otidsenliga korrelatorer". Nature Physics 14, 988–990 (2018).
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

[15] Ignacio García-Mata, Rodolfo A. Jalabert och Diego A. Wisniacki. "Otidsordning korrelatorer och kvantkaos" (2022). arXiv:2209.07965.
arXiv: 2209.07965

[16] Rahul Nandkishore och David A. Huse. "Mångkroppslokalisering och termalisering i kvantstatistisk mekanik". Annual Review of Condensed Matter Physics 6, 15–38 (2015). arXiv:1404.0686.
https: / / doi.org/ 10.1146 / annurev-conmatphys-031214-014726
arXiv: 1404.0686

[17] Dmitry A. Abanin, Ehud Altman, Immanuel Bloch och Maksym Serbyn. "Colloquium: Många kroppslokalisering, termalisering och förveckling". Reviews of Modern Physics 91, 021001 (2019). arXiv:1804.11065.
https: / / doi.org/ 10.1103 / RevModPhys.91.021001
arXiv: 1804.11065

[18] Bruno Nachtergaele och Robert Sims. "Much Ado About Something: Why Lieb-Robinson-gränser är användbara" (2011). arXiv:1102.0835.
arXiv: 1102.0835

[19] Daniel A. Roberts och Brian Swingle. "Lieb-robinson bundet och fjärilseffekten i kvantfältsteorier". Phys. Rev. Lett. 117, 091602 (2016). arXiv:1603.09298.
https: / / doi.org/ 10.1103 / PhysRevLett.117.091602
arXiv: 1603.09298

[20] Zhiyuan Wang och Kaden RA Hazzard. "Skärpning av lieb-robinson bunden i lokalt interagerande system". PRX Quantum 1, 010303 (2020). arXiv:1908.03997.
https: / / doi.org/ 10.1103 / PRXQuantum.1.010303
arXiv: 1908.03997

Citerad av

[1] Sayak Guha Roy och Kevin Slagle, "Interpolera mellan mätaren och Schrödinger bilder av kvantdynamik", SciPost Physics Core 6 4, 081 (2023).

[2] Kevin Slagle, "Quantum Gauge Networks: A New Kind of Tensor Network", Quantum 7, 1113 (2023).

Ovanstående citat är från SAO / NASA ADS (senast uppdaterad framgångsrikt 2024-03-22 22:55:39). Listan kan vara ofullständig eftersom inte alla utgivare tillhandahåller lämpliga och fullständiga citatdata.

On Crossrefs citerade service Inga uppgifter om citerande verk hittades (sista försök 2024-03-22 22:55:38).

Detta papper publiceras i Quantum under Creative Commons Attribution 4.0 International (CC BY 4.0) licens. Upphovsrätten kvarstår med de ursprungliga upphovsrättsinnehavarna som författarna eller deras institutioner.

Tidsstämpel:

Mer från Quantum Journal