หลักฐานใหม่แยกแยะ 'รูปแบบโมดูลาร์' ที่ลึกลับและทรงพลัง

ในการพิสูจน์ครั้งใหม่ วัตถุทางคณิตศาสตร์ที่ถูกละเลยมานานได้มาถึงจุดสนใจในที่สุด

เมื่อมองแวบแรก รูปแบบโมดูลาร์ ซึ่งเป็นฟังก์ชันที่มีความสมมาตรมากมายทำให้นักคณิตศาสตร์สนใจมานานหลายศตวรรษ ดูเหมือนจะได้รับความสนใจมากเกินพอ พวกเขาก่อตัวขึ้นในปัญหาทุกประเภท: พวกเขาเป็นส่วนประกอบสำคัญในการพิสูจน์ทฤษฎีบทสุดท้ายของแฟร์มาต์ในปี 1994 ของแอนดรูว์ ไวล์ส ซึ่งไขข้อข้องใจหนึ่งในคำถามเปิดที่ใหญ่ที่สุดในทฤษฎีจำนวน พวกเขามีบทบาทสำคัญใน โปรแกรมแลงแลนด์สความพยายามอย่างต่อเนื่องในการพัฒนา "ทฤษฎีคณิตศาสตร์ที่เป็นอันหนึ่งอันเดียวกัน" พวกเขาเคยถูกใช้เพื่อศึกษาแบบจำลองในทฤษฎีสตริงและฟิสิกส์ควอนตัม

แต่รูปแบบโมดูลาร์ที่เกิดขึ้นในบริบทเหล่านี้เป็นประเภทพิเศษ รูปแบบโมดูลาร์ที่เรียกว่า "สอดคล้องกัน" มีโครงสร้างเพิ่มเติมที่ทำให้ศึกษาได้ง่ายขึ้น แต่รูปแบบโมดูลาร์ทั่วไปที่ "ไม่ลงรอยกัน" นั้นมีจำนวนมากกว่ารูปแบบที่สอดคล้องกันที่เป็นมิตรกันอย่างมาก “ถ้าคุณใช้รูปแบบโมดูลาร์แบบสุ่ม ด้วยความน่าจะเป็น 1 ก็จะไม่สอดคล้องกัน” กล่าว คาเมรอน ฟรังก์นักคณิตศาสตร์แห่งมหาวิทยาลัย McMaster ในแคนาดา “ถ้าคุณไม่มีเหตุผลที่ดีจริงๆ ที่จะเจอรูปแบบโมดูลาร์ที่สอดคล้องกัน คุณก็ไม่ควรคาดหวัง พวกมันหายากมาก”

นักคณิตศาสตร์ยังรู้น้อยมากเกี่ยวกับรูปแบบโมดูลาร์ที่ไม่สอดคล้องกัน แม้ว่าพวกเขาจะแพร่หลายก็ตาม “พวกมันลึกลับมาก” กล่าว แอนโทนี่ สโคลนักคณิตศาสตร์แห่งมหาวิทยาลัยเคมบริดจ์ ไม่เพียงแต่เป็นการยากที่จะสร้างข้อความที่ครอบคลุมเกี่ยวกับคลาสทั่วไปของฟังก์ชันดังกล่าว แต่เครื่องมือที่พัฒนาขึ้นเพื่อศึกษารูปแบบโมดูลาร์จะแยกย่อยในกรณีที่ไม่สอดคล้องกัน สิ่งนี้ทำให้นักคณิตศาสตร์ไม่แน่ใจเกี่ยวกับสิ่งที่พวกเขาควรจะพยายามพิสูจน์ด้วยซ้ำ

อย่างไรก็ตาม การคาดเดาที่สำคัญอย่างหนึ่งเกี่ยวกับรูปแบบโมดูลาร์ที่ไม่สอดคล้องกันนั้นมีมานานแล้ว นั่นคือป้ายบอกทางที่โดดเดี่ยวและไม่มั่นคงในทะเลทราย

ในปี 1968 นักคณิตศาสตร์ Oliver Atkin และ Peter Swinnerton-Dyer ควรจะมีวิธีที่ชัดเจนในการแยกทั้งสองออกจากกัน "เป็นเรื่องที่น่าอัศจรรย์จริงๆ" กล่าว เจฟฟรีย์ เมสันนักคณิตศาสตร์แห่งมหาวิทยาลัยแคลิฟอร์เนีย ซานตาครูซ รูปแบบโมดูลาร์ที่สอดคล้องกันและไม่สอดคล้องกันมีความแตกต่างกันมาก เนื่องจากรูปแบบโมดูลาร์ที่ไม่สอดคล้องกันขาดความสมมาตรที่รูปแบบโมดูลาร์ที่สอดคล้องกันมี แต่ความแตกต่างเหล่านี้แม้จะสำคัญ แต่ก็ละเอียดอ่อนและตรวจจับได้ยาก

จู่ๆ ที่นี่ก็เป็นหลักฐานที่ชัดเจนของความแตกต่างเหล่านี้

การสังเกตของ Atkin และ Swinnerton-Dyer ภายหลังกลายเป็นที่รู้จักในฐานะการคาดคะเน หากเป็นจริง มันจะช่วยให้นักคณิตศาสตร์สามารถตั้งหลักได้อย่างปลอดภัยในขอบเขตของวัตถุที่ไม่สอดคล้องกันซึ่งส่วนใหญ่ยังไม่ได้สำรวจ และด้วยวิธีการที่ง่ายในการจำแนกว่ารูปแบบโมดูลาร์นั้นจัดอยู่ในคลาสใด การคาดเดายังสามารถสร้างโปรแกรมหลักในฟิสิกส์เชิงทฤษฎี ซึ่งมีเป้าหมายเพื่อทำความเข้าใจแบบจำลองของปฏิสัมพันธ์ของอนุภาคที่เรียกว่าทฤษฎีสนามคอนฟอร์มัลบนพื้นฐานทางคณิตศาสตร์ที่กระชับขึ้น

แต่เวลากว่า 50 ปี ยังไม่มีใครพิสูจน์ได้ ในที่สุดปลายปี 2021 นักคณิตศาสตร์สามคนประสบความสำเร็จ. การพิสูจน์ของพวกเขาดูเหมือนจะไม่มีที่ไหนเลย โดยใช้เทคนิคที่ไม่มีใครคาดคิดมาก่อนว่าจะได้เห็นในการศึกษาด้านนี้ นักคณิตศาสตร์และนักฟิสิกส์กำลังเริ่มสำรวจผลลัพธ์ของงานนั้น

สมมาตรและโครงสร้าง

รูปแบบโมดูลาร์ที่ไม่สอดคล้องกันไม่ได้ถูกผลักไสให้อยู่ในระยะขอบเสมอไป

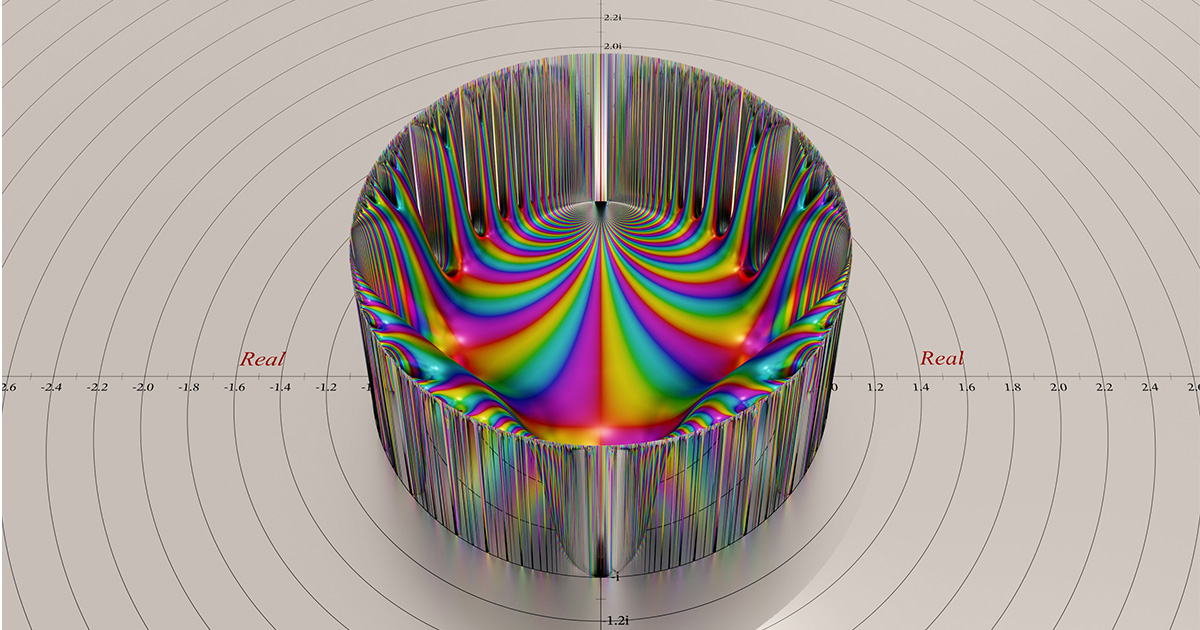
ในศตวรรษที่ 19 นักคณิตศาสตร์เพิ่งเริ่มพัฒนาทฤษฎีของรูปแบบโมดูลาร์ นี่คือชื่อที่กำหนดให้กับฟังก์ชันที่มีความสมมาตรสูงชนิดหนึ่ง ซึ่งอยู่ในโดเมนที่เรียกว่าครึ่งบนของระนาบเชิงซ้อน

ระนาบเชิงซ้อนคือวิธีการสร้างกราฟของจำนวนเชิงซ้อน ซึ่งมีสองส่วน: จำนวนจริงและจำนวนจินตภาพ รูปแบบโมดูลาร์ใช้เป็นจำนวนเชิงซ้อนที่ป้อนซึ่งส่วนจินตภาพเป็นบวก ซึ่งสอดคล้องกับครึ่งบนของระนาบ (ระนาบครึ่งบนสามารถแมปกับภายในของยูนิตดิสก์ได้อย่างง่ายดาย รูปแบบโมดูลาร์มักแสดงโดยใช้การแมปนี้)

สมมาตรจำนวนมากของรูปแบบโมดูลาร์ถูกกำหนดในแง่ของคอลเลกชันพิเศษหรือ "กลุ่ม" ของเมทริกซ์ 2 คูณ 2 - อาร์เรย์สี่เหลี่ยมของตัวเลขสี่ตัว ในรูปแบบโมดูลาร์ ตัวเลขทั้งสี่จะเป็นจำนวนเต็มเสมอ สิ่งสำคัญคือ ตัวเลขที่เกี่ยวข้องกับเมทริกซ์ที่กำหนดคุณสมบัติบางอย่าง ซึ่งเรียกว่าดีเทอร์มีแนนต์ จะต้องเป็น 1

มีชุดเมทริกซ์ดังกล่าวมากมายนับไม่ถ้วน ในบางกลุ่ม เมทริกซ์สามารถอธิบายได้ด้วยกฎที่ค่อนข้างตรงไปตรงมา ตัวอย่างเช่น ในเมทริกซ์ทั้งหมด รายการบนขวาและล่างซ้ายอาจเป็นเลขคู่ ในขณะที่อีกสองรายการที่เหลือเป็นเลขคี่ หรือบางทีรายการด้านขวาบนและด้านซ้ายล่างหารด้วย 11 ลงตัว ในขณะที่อีกสองรายการที่เหลือมีค่าเป็น 1 มากกว่าผลคูณของ 11

กลุ่มที่สามารถกำหนดได้ด้วยความสัมพันธ์ประเภทนี้ - และรูปแบบโมดูลาร์ที่เกี่ยวข้องกับกลุ่มดังกล่าว - เป็นกลุ่มที่สอดคล้องกันซึ่งมีการศึกษามาก

แต่พวกเขาก็เหมือนงมเข็มในมหาสมุทร: คอลเลกชันส่วนใหญ่ของเมทริกซ์ 2 คูณ 2 ไม่สามารถกำหนดลักษณะตามกฎที่ดีในลักษณะนี้ได้ ทำให้พวกเขาและรูปแบบโมดูลาร์ที่เกี่ยวข้องไม่สอดคล้องกัน

จนกระทั่งช่วงปลายทศวรรษที่ 1930 ซึ่งเป็นช่วงต้นของสงครามโลกครั้งที่ XNUMX การศึกษารูปแบบโมดูลาร์ที่สอดคล้องกันเริ่มบดบังการศึกษาที่ไม่สอดคล้องกัน นั่นคือตอนที่นักคณิตศาสตร์ชาวเยอรมัน Erich Hecke พัฒนากล่องเครื่องมือที่จะทำให้เขาสามารถตรึงคุณสมบัติต่างๆ ของรูปแบบโมดูลาร์และเชื่อมโยงกับวัตถุทางคณิตศาสตร์ที่สำคัญอื่นๆ ได้

วิธีการของ Hecke ใช้ได้กับกลุ่มที่สอดคล้องกันและรูปแบบโมดูลาร์เท่านั้น กลุ่มที่ไม่สอดคล้องกันขาดโครงสร้างพิเศษที่ทำให้กล่องเครื่องมือของ Hecke มีประสิทธิภาพ “สิ่งนี้ที่คุณมีในโลกแห่งความสอดคล้องกันจะออกไปเมื่อคุณก้าวไปสู่โลกที่ไม่สอดคล้องกัน” ฟรังก์กล่าว

และดูเหมือนว่ารูปแบบโมดูลาร์ที่ไม่สอดคล้องกันมักถูกมองข้ามอยู่เสมอ ไม่ได้หมายความว่าพวกมันไม่มีโครงสร้างพิเศษในตัวเอง ซุ่มซ่อนอยู่ใต้พื้นผิว ดังที่ Bryan Birch ผู้ทำงานร่วมกันของ Swinnerton-Dyer เคยเขียนไว้ว่า “แม้ว่าโครงสร้างจะลึกลับกว่า แต่ก็ดูเหมือนจะมีความสมบูรณ์พอๆ กัน” แต่เมื่อพูดถึงการเข้าถึงโครงสร้างนั้น นักคณิตศาสตร์ก็ตกอยู่ในภาวะขาดทุน พวกเขาไม่รู้ด้วยซ้ำว่าจะเริ่มจากตรงไหน

เข้าสู่ Atkin และ Swinnerton-Dyer

หลักเกณฑ์ที่เป็นระเบียบเรียบร้อย

นักคณิตศาสตร์สองคนต้องการทราบข้อมูลเพิ่มเติมเกี่ยวกับรูปแบบโมดูลาร์ที่ไม่สอดคล้องกัน และความลับที่พวกเขาอาจซ่อนไว้

"นั่นเป็นวิธีที่คณิตศาสตร์ก้าวหน้าอยู่เสมอ" กล่าว วินนี่ ลี่นักคณิตศาสตร์แห่ง Pennsylvania State University “คุณศึกษาสิ่งต่าง ๆ ที่มีคุณสมบัติพิเศษและมีโครงสร้างที่มากกว่า จากนั้นคุณก็สรุปเป็นภาพรวม เพื่อพยายามทำความเข้าใจว่าคุณสมบัติใดมีมากกว่าและคุณสมบัติใดไม่มี”

ในการศึกษารูปแบบโมดูลาร์ที่กำหนด นักคณิตศาสตร์มักแทนผลรวมที่ไม่สิ้นสุดที่เรียกว่า q-expansion (อนุกรมกำลังชนิดพิเศษ) จากนั้นจึงวิเคราะห์ค่าสัมประสิทธิ์ของการขยายตัวนั้น เป็นที่ทราบกันดีอยู่แล้วว่าหากรูปแบบโมดูลาร์ที่กำหนดมีความสอดคล้องกัน ดังนั้นค่าสัมประสิทธิ์จะมีตัวส่วนที่ไม่เคยมีค่ามากกว่าค่าคงที่ค่าหนึ่ง

ในปี 1960 Atkin และ Swinnerton-Dyer คำนวณ q-expansion สำหรับคะแนนและคะแนนของรูปแบบโมดูลาร์ ขณะที่พวกเขาทำเช่นนั้น พวกเขาสังเกตเห็นว่าหากรูปแบบโมดูลาร์ไม่สอดคล้องกัน ตัวส่วนในลำดับที่สัมพันธ์กันจะยังคงเพิ่มขึ้นโดยไม่มีขอบเขต “พวกเขาสามารถพูดอะไรบางอย่างเกี่ยวกับรูปแบบลึกลับที่ไม่สอดคล้องกันเหล่านี้ได้” กล่าว หยุนชิงถังนักคณิตศาสตร์แห่งมหาวิทยาลัยแคลิฟอร์เนีย เบิร์กลีย์

เป็นเรื่องง่ายที่จะแยกรูปแบบโมดูลาร์ทั้งสองประเภทออกจากกันอย่างง่ายดายหรือไม่?

นักคณิตศาสตร์กล่าวถึงการสังเกตของพวกเขาในการประชุมที่แคลิฟอร์เนียในปี พ.ศ. 1968 ซึ่งบ่งชี้ว่าตัวส่วนที่ไม่มีขอบเขตอาจเป็นลักษณะทั่วไปของรูปแบบโมดูลาร์ที่ไม่สอดคล้องกัน การคาดเดานั้น “น่าทึ่งมาก” กล่าว จอห์น วอยต์นักคณิตศาสตร์ที่ Dartmouth College “มันทำให้เรามีเกณฑ์ที่เป็นระเบียบเรียบร้อยในการตัดสินใจว่ารูปแบบโมดูลาร์เป็นของกลุ่มที่สอดคล้องกันหรือไม่” ซึ่งเป็นการทดสอบกระดาษลิตมัสที่สะดวกมากสำหรับนักทฤษฎีจำนวน และบางอย่างที่ในบริบทอื่นอาจตรวจจับได้ยาก

“มันเกือบจะดีเกินกว่าจะเป็นจริง” เขากล่าวเสริม “ไม่มีใครคาดหวังปาฏิหาริย์แบบนั้นจริงๆ”

แท้จริงแล้ว ไม่มีใครสามารถพิสูจน์การคาดคะเนของตัวส่วนที่ไม่มีขอบเขตได้ หลี่และอีกไม่กี่คนเคยเป็น สามารถแสดง มันเป็นความจริงสำหรับ ครอบครัวเฉพาะ ของรูปแบบโมดูลาร์ที่ไม่สอดคล้องกัน แต่นักคณิตศาสตร์ไม่รู้ว่าจะจัดการกับข้อความทั่วไปอย่างไร

จากนั้นในเดือนกันยายน 2021 Tang พร้อมด้วย แฟรงค์ คัลการี ของมหาวิทยาลัยชิคาโกและ เวสเซลิน ดิมิทรอฟ ของสถาบันการศึกษาขั้นสูงโพสต์หลักฐาน 50 หน้า “มันน่าทึ่งและเหนือความคาดหมายจริงๆ” ฟรังก์กล่าว “รู้สึกเหมือนว่าชุมชนไม่มีความคิดว่าจะจัดการกับปัญหานี้อย่างไร”

ผู้เขียนหวังว่าเอกสารของพวกเขาจะเป็นก้าวแรกในการพัฒนาป้ายบอกทางในทะเลทรายให้เป็นเครือข่ายถนนที่เต็มเปี่ยม Dimitrov กล่าวว่า "เรามีส่วนร่วมเล็กน้อยในส่วนนี้ของทฤษฎีจำนวนโดยให้คำตอบสำหรับคำถามที่ง่ายที่สุด

กลับสู่วิธีเก่า

คาเลการี ดิมิทรอฟ และถังไม่ได้ตั้งใจที่จะแก้ปัญหาการคาดคะเนของตัวส่วนที่ไม่มีขอบเขต ในช่วงปลายปี 2019 พวกเขาหวังว่าจะแสดงให้เห็นว่าจำนวนหนึ่ง (ค่าของอะนาลอกของฟังก์ชันซีตาของ Riemann) เป็นจำนวนอตรรกยะ — นั่นคือ เช่นเดียวกับรากที่สองของ 2 ที่ไม่สามารถเขียนเป็นเศษส่วนได้ (เป้าหมายสูงสุดของพวกเขาคือการพิสูจน์ว่าตัวเลขนี้และตัวเลขอื่นๆ π และ eไม่สามารถเขียนเป็นคำตอบของสมการพหุนามที่มีสัมประสิทธิ์จำนวนเต็มได้)

ปัญหานี้ไม่เกี่ยวข้องกันโดยสิ้นเชิง แต่ในวันที่ 1 มกราคม 2021 ดิมิทรอฟส่งอีเมลถึงคนอื่นๆ ในช่วงปีใหม่ โดยเขาอธิบายว่า "เป็นความคิดที่ปรารถนา": บางทีเทคนิคที่พวกเขาพัฒนาขึ้นในปีที่แล้วอาจถูกนำมาใช้ใหม่เพื่อพิสูจน์การคาดคะเนของตัวส่วนที่ไม่มีขอบเขต

พวกเขาให้มันยิง ภายในเจ็ดเดือน พวกเขาก็มีหลักฐาน

ประการแรก พวกเขาพิจารณาช่องว่างสองช่อง: ช่องว่างของรูปแบบโมดูลาร์ทั้งหมดที่มีตัวส่วนล้อมรอบ และพื้นที่ของรูปแบบโมดูลาร์ที่สอดคล้องกันทั้งหมด ตามการคาดคะเนของตัวส่วนที่ไม่มีขอบเขต ช่องว่างทั้งสองนั้นควรจะเหมือนกัน เนื่องจากช่องว่างเป็นไปตามคุณสมบัติบางประการ นักคณิตศาสตร์จึงต้องแสดงว่าพวกมันมีขนาดเท่ากันเท่านั้น การทำเช่นนั้นจะบ่งบอกถึงความเท่าเทียมกันโดยอัตโนมัติ

Calegari, Dimitrov และ Tang สามารถคำนวณขนาดของช่องว่างที่สองได้ค่อนข้างง่าย โดยได้รับรูปแบบโมดูลาร์ที่สอดคล้องกันแบบคร่าวๆ แต่มันยากมากที่จะประเมินขนาดของช่องว่างแรก พวกเขาต้องผสมผสานเทคนิคต่างๆ มากมาย รวมทั้งเทคนิคจากทฤษฎีจำนวนเหนือธรรมชาติ

เมื่อใช้วิธีการเหล่านั้น พวกเขาแสดงให้เห็นว่าพื้นที่ของรูปแบบโมดูลาร์ที่มีตัวส่วนล้อมรอบอาจมีขนาดสูงสุดที่แน่นอนได้ ขนาดสูงสุดนั้นใหญ่กว่าขนาดของช่องว่างของรูปแบบโมดูลาร์ที่สอดคล้องกันเล็กน้อย ถึงกระนั้น ขั้นตอนนี้กลายเป็น "หัวใจของการพิสูจน์อย่างแท้จริง" กล่าว ฌอง-เบอนัวต์ บอสต์นักคณิตศาสตร์แห่งมหาวิทยาลัย Paris-Saclay “คุณต้องมีความอดทนอย่างมากในการทำเช่นนั้น” (Calegari, Dimitrov และ Tang ได้พิสูจน์ขอบเขตนี้กับขนาดของพื้นที่ด้วยวิธีต่างๆ มากมาย ซึ่งอาจทำให้เทคนิคของพวกเขานำไปใช้ได้กว้างขึ้น)

“มันเป็นคณิตศาสตร์ที่สวยงาม คลาสสิกมาก และมีกลิ่นอายของศตวรรษที่ 19” กล่าว ฮาเวียร์ เฟรซานนักคณิตศาสตร์ที่ École Polytechnique ในฝรั่งเศส

จากนั้นทั้งสามคนจำเป็นต้องปิดช่องว่างระหว่างช่องว่างทั้งสอง การทำเช่นนี้จะพิสูจน์ได้ว่ารูปแบบโมดูลาร์ใดๆ ที่มีตัวส่วนที่มีขอบเขตจะต้องสอดคล้องกัน

ดังนั้นพวกเขาจึงถือว่าตรงกันข้าม: มีรูปแบบโมดูลาร์ที่ไม่สอดคล้องกันซึ่งมีตัวส่วนล้อมรอบ ตามคำนิยาม มันจะอยู่ในช่องว่างที่ Calegari, Dimitrov และ Tang พยายามปิด ทั้งสามแสดงให้เห็นว่าการมีอยู่ของรูปแบบโมดูลาร์ที่ไม่สอดคล้องกันนี้บ่งบอกถึงการมีอยู่ของรูปแบบโมดูลาร์ที่ไม่สอดคล้องกันอื่นๆ จำนวนมากที่มีตัวส่วนที่มีขอบเขตโดยอัตโนมัติ ราวกับว่าป่าทั้งป่าเติบโตจากเมล็ดพืชเพียงเมล็ดเดียว

แต่พวกเขาได้กำหนดขนาดสูงสุดของช่องว่างแล้ว และมันเล็กเกินไปที่จะพอดีกับรูปแบบที่ไม่สอดคล้องกันจำนวนมากนั้น

ซึ่งหมายความว่าแม้แต่รูปแบบเดียวก็ไม่สามารถมีอยู่ได้ พวกเขาต้องการพิสูจน์การคาดคะเนหลายสิบปีของ Atkin และ Swinnerton-Dyer

นักคณิตศาสตร์พบว่าเทคนิคต่างๆ ที่ใช้ในงานน่าสนใจยิ่งกว่าผลลัพธ์เสียอีก Scholl กล่าวว่า "ความคิดเหล่านี้ไม่เคยถูกนำมาใช้มาก่อนในการศึกษาเลขคณิตของรูปแบบโมดูลาร์

ดังที่ Voight อธิบาย แม้ว่าการศึกษารูปแบบโมดูลาร์จะเริ่มต้นขึ้นโดยเป็นส่วนหนึ่งของการวิเคราะห์เชิงซ้อน แต่งานปัจจุบันคือขอบเขตของทฤษฎีจำนวนและเรขาคณิตเชิงพีชคณิต เขากล่าวว่าบทความฉบับใหม่นี้เป็นการย้อนกลับไปสู่การวิเคราะห์ที่ซับซ้อน: "มันเป็นมุมมองแบบเก่าที่สดชื่น"

การค้นหาทฤษฎีใหม่

ไม่ใช่นักคณิตศาสตร์คนเดียวที่ตื่นเต้นกับการคาดคะเนตัวส่วนที่ไม่มีขอบเขต นอกจากนี้ยังปรากฏในฟิสิกส์เชิงทฤษฎี

ในปี 1970 มีเรื่องอื่นเกิดขึ้นควบคู่ไปกับเรื่องที่เริ่มต้นโดย Atkin และ Swinnerton-Dyer นักคณิตศาสตร์มี สังเกตเห็นการเชื่อมต่อที่แปลกประหลาด ระหว่างวัตถุที่เรียกว่ากลุ่มสัตว์ประหลาดและรูปแบบโมดูลาร์ที่เรียกว่า j-การทำงาน. ค่าสัมประสิทธิ์ของ j-ฟังก์ชั่นสะท้อนถึงคุณสมบัติบางอย่างของกลุ่มมอนสเตอร์ได้อย่างแม่นยำ

การวิจัยในภายหลังเปิดเผยว่าการเชื่อมต่อนี้เกิดจากความจริงที่ว่าทั้งกลุ่มและรูปแบบโมดูลาร์มีความสัมพันธ์กับแบบจำลองที่สำคัญของการปฏิสัมพันธ์ของอนุภาคที่เรียกว่าทฤษฎีสนามคอนฟอร์มัลแบบสองมิติ

แต่ทฤษฎีสนามคอนฟอร์มัลที่เชื่อมโยงกลุ่มสัตว์ประหลาดเข้ากับ j-ฟังก์ชันเป็นเพียงตัวอย่างหนึ่งของทฤษฎีสนามคอนฟอร์มัลจำนวนไม่สิ้นสุด และแม้ว่าทฤษฎีเหล่านี้ไม่ได้อธิบายถึงจักรวาลที่เราอาศัยอยู่ แต่การทำความเข้าใจกับสิ่งเหล่านี้สามารถให้ความเข้าใจใหม่ ๆ ว่าทฤษฎีสนามควอนตัมที่สมจริงยิ่งขึ้นอาจมีพฤติกรรมอย่างไร

ดังนั้นนักฟิสิกส์จึงยังคงศึกษาทฤษฎีสนามที่สอดคล้องกันโดยดูที่รูปแบบโมดูลาร์ที่เกี่ยวข้อง (ในบริบทนี้ นักฟิสิกส์ใช้แนวคิดทั่วไปเกี่ยวกับรูปแบบโมดูลาร์ที่เรียกว่ารูปแบบโมดูลาร์ที่มีค่าเวกเตอร์)

เพื่อจัดการกับสิ่งที่เกิดขึ้นกับทฤษฎีสนามคอนฟอร์มัลโดยเฉพาะ คุณต้องแสดงให้เห็นว่ารูปแบบโมดูลาร์ของมันสอดคล้องกัน กล่าว ไมเคิล ทูอิทนักคณิตศาสตร์และนักฟิสิกส์เชิงทฤษฎีที่มหาวิทยาลัยกัลเวย์ในไอร์แลนด์ จากนั้นคุณสามารถเริ่มอธิบายทฤษฎีสนามที่สอดคล้องกัน และแม้แต่ค้นพบสิ่งใหม่ๆ ที่คุณไม่รู้จักเพื่อค้นหา นี่เป็นสิ่งสำคัญอย่างยิ่งสำหรับความพยายามอย่างต่อเนื่องในการจำแนกทฤษฎีสนามที่สอดคล้องกันทั้งหมด ซึ่งเป็นโครงการที่นักฟิสิกส์ได้ขนานนามว่าบูทสแตรปแบบโมดูลาร์

"เมื่อคุณรู้ว่ามันเป็นรูปแบบโมดูลาร์ที่สอดคล้องกัน ซึ่งจะทำให้คุณสามารถก้าวหน้าอย่างมากในโปรแกรมนี้ได้" เมสันกล่าว

นักฟิสิกส์ได้พัฒนากรอบที่ช่วยให้พวกเขายอมรับคุณสมบัติความสอดคล้องนี้สำหรับรูปแบบโมดูลาร์ที่พวกเขากำลังศึกษาอยู่ แต่นั่นก็ไม่เหมือนกับการมีหลักฐานทางคณิตศาสตร์ที่เข้มงวด — และในขณะที่นักคณิตศาสตร์คนอื่นๆ แสดงหลักฐานดังกล่าวอาร์กิวเมนต์ของพวกเขาใช้ได้เฉพาะในการตั้งค่าบางอย่างเท่านั้น นอกจากนี้ยังเกี่ยวข้องกับ "เส้นทางที่คดเคี้ยวและซับซ้อนมาก" ไปสู่ความสอดคล้องตามที่ Mason กล่าว แม้ว่าเขาจะยังชี้ให้เห็นว่าเส้นทางที่คดเคี้ยวนี้ให้ข้อมูลเชิงลึกที่สำคัญ

การพิสูจน์ของ Calegari, Dimitrov และ Tang เกี่ยวกับการคาดคะเนของตัวส่วนที่ไม่มีขอบเขตทำให้ทุกอย่างจบลง นั่นเป็นเพราะว่า ตามที่ปรากฏ รูปแบบโมดูลาร์ที่เกี่ยวข้องกับทฤษฎีฟิลด์ที่สอดคล้องกันจะมีค่าสัมประสิทธิ์จำนวนเต็มเสมอ ตามคำนิยาม จำนวนเต็มมีตัวส่วนเป็น 1 หมายความว่าตัวส่วนมีขอบเขตเสมอ และเนื่องจากการคาดคะเนของตัวส่วนที่ไม่มีขอบเขตระบุว่าตัวส่วนที่มีขอบเขตเกี่ยวข้องเฉพาะกับรูปแบบโมดูลาร์ที่สอดคล้องกันเท่านั้น จึงไม่จำเป็นต้องตั้งสมมติฐานอีกต่อไป “คุณไม่จำเป็นต้องรู้อะไรเกี่ยวกับ [conformal field theories] เลยด้วยซ้ำ” Tang กล่าว หลักฐานใหม่จะมอบความสอดคล้องโดยอัตโนมัติสำหรับกรณีเหล่านี้ทั้งหมด — ฟรี

“มันเป็นสิ่งที่อยู่ในอากาศมานานหลายทศวรรษ” บอสท์กล่าว ตอนนี้ก็แก้ไขได้ในที่สุด

“มันเป็นเรื่องมหัศจรรย์จริงๆ” เมสันกล่าว “นี่เป็นไปตามข้อเท็จจริงที่ว่าลำดับเหล่านี้เป็นจำนวนเต็มอย่างน่าอัศจรรย์”

เขาเริ่มนำผลลัพธ์ไปใช้ในงานของเขาเองแล้ว “นับตั้งแต่วันที่กระดาษปรากฏขึ้น ผมก็ใช้ประโยชน์จากมัน” เขากล่าว “มันเป็นทางลัดที่น่ายินดีมากสำหรับผลลัพธ์ที่ฉันต้องการแก้ไข …มันกำลังตัดงานที่มีศักยภาพจำนวนมากซึ่งผมมองไม่เห็นทางออกไป”

นอกจากนี้ยังทำให้โปรแกรมบูทสแตรปแบบโมดูลาร์และผลลัพธ์อื่น ๆ บนพื้นฐานทางคณิตศาสตร์ที่แข็งแกร่งยิ่งขึ้น “นี่จะทำให้นักคณิตศาสตร์สามารถพิสูจน์ผลลัพธ์ [ก่อนหน้า] ได้อีกครั้ง หรือเชื่อในผลลัพธ์เหล่านั้น” เมสันกล่าว

“ฉันคิดว่ามันจะมีผลกระทบจริงๆ โดยเฉพาะอย่างยิ่งในด้านคณิตศาสตร์ เพื่อเชื่อมโยงสิ่งต่างๆ เข้าด้วยกันจริงๆ เพื่อทำความเข้าใจอย่างถ่องแท้ว่าเกิดอะไรขึ้น” Tuite กล่าว

วิชชาทางคณิตศาสตร์

ในปีที่พวกเขาโพสต์หลักฐาน Calegari, Dimitrov และ Tang ยังคงทำงานร่วมกันต่อไป ตอนนี้พวกเขากลับมาที่ประเภทของปัญหาในทฤษฎีจำนวนอดิศัย ซึ่งแต่เดิมจุดประกายความสนใจของพวกเขาในการคาดเดา “เรากำลังพยายามทำสิ่งที่เราเริ่มต้นให้เสร็จ” Tang กล่าว อันที่จริง พวกเขาใช้เทคนิคของตนเพื่อพิสูจน์ว่าจำนวนดอกเบี้ยหลายตัวไม่มีเหตุผล

“พวกเขากำลังผลักดัน [วิธีการ] ให้ถึงขีดจำกัดจริงๆ” Fresán กล่าว “ฉันตื่นเต้นมากเกี่ยวกับเรื่องนี้”

วิธีการเหล่านี้อาจใช้ได้กับปัญหาอื่นๆ ในทฤษฎีจำนวนด้วย

นอกเหนือจากเทคนิคแล้ว ความละเอียดของการคาดคะเนของตัวส่วนที่ไม่มีขอบเขตถือเป็นหนึ่งในหลักชัยสำคัญประการแรกในความพยายามที่จะได้รับความเข้าใจที่ดีขึ้นเกี่ยวกับรูปแบบโมดูลาร์ที่ไม่สอดคล้องกัน “นี่เป็นความสำเร็จที่น่าทึ่ง ที่เราสามารถก้าวหน้าในรูปแบบที่ไม่สอดคล้องกันได้ด้วยวิธีนี้” ฟรังก์กล่าว “ฉันตื่นเต้นสำหรับอีก 10, 20 ปีข้างหน้าเพื่อดูว่าจะเกิดอะไรขึ้น”

Li, Voight และคนอื่นๆ เริ่มมองหารูปแบบในรูปแบบของตัวเลขที่ปรากฏในตัวส่วนในรูปแบบโมดูลาร์ลึกลับเหล่านี้แล้ว พวกเขาหวังว่าในการทำเช่นนั้น พวกเขาสามารถค้นหาคำใบ้ของโครงสร้างที่ลึกลงไปได้

“การคาดคะเนตัวส่วนที่ไม่มีขอบเขตนี้เป็นเพียงจุดเริ่มต้น” หลี่กล่าว