1ICFO-Institut de Ciencies Fotoniques, Barselona Bilim ve Teknoloji Enstitüsü, 08860 Castelldefels, İspanya
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barselona, İspanya
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, Fransa
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barselona, İspanya
Bu makaleyi ilginç mi buldunuz yoksa tartışmak mı istiyorsunuz? SciRate'e çığlık at veya yorum bırak.
Özet
Karşılıklı tarafsız bazlar, kuantum bilgi teorisinde son derece yararlı ölçüm çiftlerine karşılık gelir. En küçük bileşik boyut olan altıda, üç ila yedi arasında karşılıklı olarak tarafsız bazın var olduğu biliniyor; Zauner varsayımı olarak bilinen ve en fazla üç tanenin var olduğunu belirten onlarca yıllık bir varsayımla. Burada Zauner'in varsayımını sayısal olarak, $n,d ge 2$ boyutunda $n$ boyutunda maksimum düzeyde ihlal edilebilecek her $n,d ge 83$ tamsayı çifti için Bell eşitsizliklerinin oluşturulması yoluyla ele alıyoruz; ancak ve ancak bu boyutta $n$ MUB'lar mevcutsa. Dolayısıyla Zauner'in varsayımını üç sayısal yöntemle ele aldığımız bir optimizasyon problemine dönüştürüyoruz: tahterevalli optimizasyonu, doğrusal olmayan yarı kesin programlama ve Monte Carlo teknikleri. Her üç yöntem de düşük boyutlardaki bilinen durumları doğru bir şekilde tanımlar ve tümü, altıncı boyutta karşılıklı olarak tarafsız dört tabanın bulunmadığını ve hepsi karşılık gelen Bell eşitsizliğini sayısal olarak optimize eden aynı tabanları bulduğunu öne sürer. Dahası, bu sayısal iyileştiriciler, [P. 062303'deki bir mesafe ölçüsünün sayısal olarak optimize edilmesi yoluyla bulunan, altıncı boyuttaki "en uzak dört taban" ile çakışıyor gibi görünmektedir. Raynal, X. Lü, B.-G. Englert, {Phys. Rev. A}, { 2011} XNUMX (XNUMX)]. Son olarak, Monte Carlo sonuçları onuncu boyutta en fazla üç MUB'un mevcut olduğunu göstermektedir.
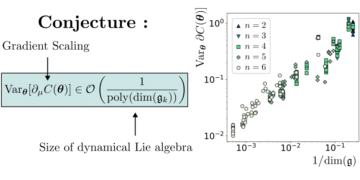
Öne çıkan görsel: d boyutunda n MUB olduğu varsayılarak Bell eşitsizliklerimizin değeri ile sayısal yöntemlerimiz tarafından bulunan değer arasındaki göreli fark. Sıfır değerler, yöntemlerin d boyutunda n MUB bulduğunu, sıfır olmayan değerler ise yöntemlerin d boyutunda n MUB bulamadığını gösterir. Bilinen tüm vakalar (iki ila beş boyutlar ve iki ve üç MUB'lu altıncı boyut) sayısal değerlerle doğru bir şekilde tanımlanır. Altıncı boyutta, yöntemlerin hiçbiri dört MUB bulamaz ve tüm yöntemler aynı dört temel kümesine yakınsar.
Popüler özet
Yaygın kullanımlarına rağmen MUB'ların yapısına ilişkin hala cevaplanmamış sorular bulunmaktadır. En belirgin olanı, kuantum sisteminin boyutu bileşik bir sayı ise çift taraflı tarafsız olan maksimum ölçüm sayısı (“MUB sayısı”) bilinmemektedir. Özellikle altıncı boyutta sadece MUB sayısının üç ile yedi arasında olduğunu biliyoruz. Uzun süredir devam eden açık bir varsayım, Zauner'in altıncı boyutta üçten fazla MUB bulunmadığını belirtmesidir. Onlarca yıldır süren bu varsayım, bazı sayısal delillerle destekleniyor ancak bugüne kadar elde edilmiş bir delil yok.
Bu çalışmada Zauner'in varsayımını Bell'in yerel olmaması üzerinden ele alıyoruz. Bell'in yerel olmaması, iletişim kurmasına izin verilmeyen ancak klasik rastgelelik veya paylaşılan kuantum durumu biçiminde bazı korelasyonları paylaşabilen iki deneyciyle ilgilidir. Kuantum kaynaklarının paylaşılmasının, klasik fizikle (daha doğrusu yerel gizli değişken modelleri olarak adlandırılanlarla) açıklanamayan deneysel verilere yol açabileceği gösterilmiştir. Bu Bell teoremi olarak bilinir ve son on yılda deneysel olarak doğrulanmıştır. Deneysel verilerin klasik olmadığına tanıklık etmek en yaygın olarak deneyde meydana gelen ölçüm sonucu olasılıklarının işlevleri olan Bell eşitsizlikleri aracılığıyla yapılır. Klasik veriler Bell eşitsizliklerini karşılamalıdır; kuantum verileri ise bunları ihlal edebilir.
Son zamanlarda, taraflardan biri belirli bir boyutta bir çift MUB ölçümü kullanırsa, Bell eşitsizliklerinin maksimum düzeyde ihlal edildiği bulunmuştur. Bu çalışmada, bu eşitsizlikleri, belirli bir boyutta seçilen sayıda MUB ölçümü tarafından maksimum düzeyde ihlal edilen yeni eşitsizliklere genişletiyoruz. Ayrıca, deneydeki boyut sabitse, maksimum ihlal, ancak ve ancak kullanılan ölçümlerin verilen boyutta seçilen MUB sayısına karşılık gelmesi durumunda elde edilir. Bu nedenle, belirli bir boyutta seçilen sayıda MUB olup olmadığına karar vermek, bu sabit boyutta karşılık gelen Bell eşitsizliğinin maksimum ihlalini bulmaya eşdeğerdir.
Bu maksimum ihlali bulmak genel olarak zor bir problem olsa da, sabit bir boyutta Bell eşitsizliklerimizin maksimum ihlalini bulmak için üç farklı sayısal yöntem kullanıyoruz. Bu yöntemlerden ikisi yarı kesin programlama tekniklerinin varyantlarıdır, üçüncüsü ise istatistiksel fizikten ilham alır ve tavlama benzetimi olarak adlandırılır. Bu yöntemlerin tümü buluşsal olsa da (yani, problemin gerçek optimumunu bulacağının garantisi yoktur), optimumu bilinen optimizasyon problemlerine bunları uygulayarak performanslarını ölçebilirsiniz. Özellikle, her üç yöntemin de MUB ölçümlerini, var olduğu bilinen durumlarda doğru şekilde tanımlayabildiğini bulduk. Ayrıca, var olmadıklarının bilindiği durumlarda, her üç yöntem de sayısal kesinliğe kadar aynı ölçüm setine yakınsar. Daha sonra yöntemlerimizi ilk bilinmeyen duruma, yani altıncı boyuttaki dört MUB'a uyguluyoruz. Yöntemlerin hiçbiri altıncı boyuttaki dört MUB'u tanımlayamıyor ancak yine de hepsi sayısal kesinliğe kadar aynı dört ölçüm kümesine yakınsıyor. Ayrıca, benzetilmiş tavlama tekniği bir sonraki bileşik boyut olan onuncu boyutta dört MUB bulamaz. Bu nedenle, tekniklerimizin buluşsal doğası nedeniyle kesin iddialarda bulunulamazken, sonuçlarımız Zauner'in Bell'in yerel olmayışına ilişkin yeni perspektiften yaptığı varsayımı desteklemektedir.
► BibTeX verileri
► Referanslar
[1] Kimlik İvanoviç. Kuantal durum belirlemenin geometrik açıklaması. Journal of Physics A: Mathematical and General, 14(12):3241–3245, 1981. doi:10.1088/0305-4470/14/12/019.
https://doi.org/10.1088/0305-4470/14/12/019
[2] G. Brassard CH Bennett. Kuantum kriptografi: Genel anahtar dağıtımı ve yazı tura atma. IEEE Uluslararası Bilgisayarlar, Sistemler ve Sinyal İşleme Konferansı Tutanakları (IEEE, 1984), 175:8, 1984. doi:10.1016/j.tcs.2011.08.039.
https: / / doi.org/ 10.1016 / j.tcs.2011.08.039
[3] Artur K. Ekert. Bell teoremine dayanan kuantum kriptografisi. Fizik. Rev. Lett., 67:661–663, 1991. doi:10.1103/PhysRevLett.67.661.
https: / / doi.org/ 10.1103 / PhysRevLett.67.661
[4] Dagmar Bruß. Altı durumlu kuantum kriptografisinde optimum gizli dinleme. fizik Rev. Lett., 81:3018–3021, 1998. doi:10.1103/PhysRevLett.81.3018.
https: / / doi.org/ 10.1103 / PhysRevLett.81.3018
[5] Armin Tavakoli, Alley Hameedi, Breno Marques ve Mohamed Bourennane. Tek $d$-seviyeli sistemler kullanan kuantum rasgele erişim kodları. fizik Rev. Lett., 114:170502, 2015. doi:10.1103/PhysRevLett.114.170502.
https: / / doi.org/ 10.1103 / PhysRevLett.114.170502
[6] Máté Farkas ve Jędrzej Kaniewski. Hazırla ve ölç senaryosunda karşılıklı tarafsız bazları kendi kendine test etme. fizik Rev. A, 99:032316, 2019. doi:10.1103/PhysRevA.99.032316.
https: / / doi.org/ 10.1103 / PhysRevA.99.032316
[7] H. Bechmann-Pasquinucci ve N. Gisin. İkili ölçümlerle kunit için çan eşitsizliği. Kuantum Bilgisi. Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https: / / doi.org/ 10.26421 / QIC3.2-6
[8] Jędrzej Kaniewski, Ivan Šupić, Jordi Tura, Flavio Baccari, Alexia Salavrakos ve Remigiusz Augusiak. Maksimal dolaşıklıktan ve karşılıklı tarafsız tabanlardan maksimum yerel olmama ve iki kütritlik kuantum sistemlerinin kendi kendini sınaması. Quantum, 3:198, 2019. doi:10.22331/q-2019-10-24-198.
https://doi.org/10.22331/q-2019-10-24-198
[9] Armin Tavakoli, Máté Farkas, Denis Rosset, Jean-Daniel Bancal ve Jędrzej Kaniewski. Bell deneylerinde karşılıklı tarafsız tabanlar ve simetrik bilgisel olarak tam ölçümler. Science Advances, 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847.
https://doi.org/10.1126/sciadv.abc3847
[10] Thomas Durt, Berthold-Georg Englert, Ingemar Bengtsson ve Karol Życzkowski. Karşılıklı tarafsız temellerde. International Journal of Quantum Information, 08(04):535–640, 2010. doi:10.1142/S0219749910006502.
https: / / doi.org/ 10.1142 / S0219749910006502
[11] William K. Wootters ve Brian D. Fields. Karşılıklı tarafsız ölçümlerle optimum durum belirleme. Annals of Physics, 191(2):363–381, 1989. doi:10.1016/0003-4916(89)90322-9.
https://doi.org/10.1016/0003-4916(89)90322-9
[12] Paweł Wocjan ve Thomas Beth. Kare ölçülerde karşılıklı olarak yansız bazaların yeni konstrüksiyonu. Kuantum Bilgisi. Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1.
https: / / doi.org/ 10.26421 / QIC5.2-1
[13] Mihaly Weiner. Karşılıklı tarafsız bazların maksimum sayısı için bir boşluk. Proc. Amr. Matematik. Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5.
https://doi.org/10.1090/S0002-9939-2013-11487-5
[14] Gerhard Zauner. Quantendesigns: Grundzüge einer nichtkommutativen Designtheorie. Doktora tezi, 1999.
[15] P. Oscar Boykin, Meera Sitharam, Pham Huu Tiep ve Pawel Wocjan. Lie cebirlerinin karşılıklı yansız tabanları ve ortogonal ayrışımları. Kuantum Bilgisi. Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https: / / doi.org/ 10.26421 / QIC7.4-6
[16] Stephen Brierley ve Stefan Weigert. Altıncı boyutta karşılıklı tarafsız üsler inşa etmek. fizik Rev. A, 79:052316, 2009. doi:10.1103/PhysRevA.79.052316.
https: / / doi.org/ 10.1103 / PhysRevA.79.052316
[17] Philippe Jaming, Máté Matolcsi, Péter Móra, Ferenc Szöllősi ve Mihály Weiner. Genelleştirilmiş bir Pauli problemi ve 6. boyutta sonsuz bir MUB üçlüsü ailesi. Journal of Physics A: Mathematical and Theoretical, 42(24):245305, mayıs 2009. doi:10.1088/1751-8113/42/24/ 245305.
https://doi.org/10.1088/1751-8113/42/24/245305
[18] Gary McConnell, Harry Spencer ve Afaq Tahir. $mathbb{C}^6$'da Zauner'in MUB varsayımını destekleyen ve ona karşı çıkan kanıtlar. 2021. doi:10.48550/arXiv.2103.08703.
https://doi.org/10.48550/arXiv.2103.08703
[19] Sander Gribling ve Sven Polak. Karşılıklı tarafsız bazlar: polinom optimizasyonu ve simetri. 2021. doi:10.48550/arXiv.2111.05698.
https://doi.org/10.48550/arXiv.2111.05698
[20] Ingemar Bengtsson, Wojciech Bruzda, Åsa Ericsson, Jan-Åke Larsson, Wojciech Tadej ve Karol Życzkowski. Karşılıklı tarafsız bazlar ve altıncı dereceden Hadamard matrisleri. Journal of Mathematical Physics, 48(5):052106, 2007. doi:10.1063/1.2716990.
https: / / doi.org/ 10.1063 / 1.2716990
[21] Philippe Raynal, Xin Lü ve Berthold-Georg Englert. Altı boyutta karşılıklı tarafsız bazlar: En uzak dört baz. fizik Rev. A, 83:062303, 2011. doi:10.1103/PhysRevA.83.062303.
https: / / doi.org/ 10.1103 / PhysRevA.83.062303
[22] Edgar A. Aguilar, Jakub J. Borkała, Piotr Mironowicz ve Marcin Pawłowski. Karşılıklı tarafsız bazlar ve kuantum rasgele erişim kodları arasındaki bağlantılar. fizik Rev. Lett., 121:050501, 2018. doi:10.1103/PhysRevLett.121.050501.
https: / / doi.org/ 10.1103 / PhysRevLett.121.050501
[23] Nicolas Brunner, Daniel Cavalcanti, Stefano Pironio, Valerio Scarani ve Stephanie Wehner. Bell yersizliği. Rev. Modu. Phys., 86:419–478, 2014. doi:10.1103/RevModPhys.86.419.
https: / / doi.org/ 10.1103 / RevModPhys.86.419
[24] MOSEK ApS. C++ 9.2.49 için MOSEK Fusion API, 2021. URL: https:///docs.mosek.com/9.2/cxxfusion/index.html.
https:///docs.mosek.com/9.2/cxxfusion/index.html
[25] Hiroshi Yamashita, Hiroshi Yabe ve Kouhei Harada. Doğrusal olmayan yarı kesin programlama için bir asal-ikili iç nokta yöntemi. Matematiksel programlama, 135(1):89–121, 2012. doi:10.1007/s10107-011-0449-z.
HTTPS: / / doi.org/ 10.1007 / s10107-011-0449-z
[26] Stephen Boyd ve Lieven Vandenberghe. Dışbükey Optimizasyon. Cambridge University Press, 2004. doi: 10.1017 / CBO9780511804441.
https: / / doi.org/ 10.1017 / CBO9780511804441
[27] S. Kirkpatrick, CD Gelatt ve MP Vecchi. Simüle tavlama ile optimizasyon. Science, 220(4598):671–680, 1983. doi:10.1126/science.220.4598.671.
https: / / doi.org/ 10.1126 / science.220.4598.671
[28] Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller ve Edward Teller. Hızlı hesaplama makineleri ile durum hesaplamalarının denklemi. The Journal of Chemical Physics, 21(6):1087–1092, 1953. doi:10.1063/1.1699114.
https: / / doi.org/ 10.1063 / 1.1699114
[29] Miguel Navascués, Stefano Pironio ve Antonio Acín. Kuantum bağıntıları kümesini sınırlamak. fizik Rev. Lett., 98:010401, 2007. doi:10.1103/PhysRevLett.98.010401.
https: / / doi.org/ 10.1103 / PhysRevLett.98.010401
Alıntılama
Bu Makale, Quantum'da Creative Commons Atıf 4.0 Uluslararası (CC BY 4.0) lisans. Telif hakkı, yazarlar veya kurumları gibi orijinal telif hakkı sahiplerine aittir.