1انسٹی ٹیوٹ فار تھیوریٹیکل فزکس، یونیورسٹی آف انسبرک، ٹیکنکرسٹر۔ 21A، 6020 انسبرک، آسٹریا
2شعبہ طبیعیات، QAA، ٹیکنیکل یونیورسٹی آف میونخ، James-Franck-Str. 1، D-85748 گارچنگ، جرمنی
3موجودہ پتہ: Atominstitut, Technische Universität Wien, Stadionallee 2, 1020 Vienna, Austria
4Departamento de Matemáticas, Universidad Carlos III de Madrid, Avda. de la Universidad 30, E-28911, Leganés (Madrid), Spain
5Instituto de Ciencias Matemáticas (ICMAT), E-28049 میڈرڈ، سپین
اس کاغذ کو دلچسپ لگتا ہے یا اس پر بات کرنا چاہتے ہیں؟ SciRate پر تبصرہ کریں یا چھوڑیں۔.
خلاصہ
کلاسیکی کمیونیکیشن (LOCC) کی مدد سے مقامی آپریشنز کے ساتھ مقامی طور پر الگ پارٹیوں کے ذریعے ریاستی تبدیلیوں کا مطالعہ کوانٹم انفارمیشن پروسیسنگ میں الجھانے کے نظریہ اور اس کے اطلاق میں ایک اہم کردار ادا کرتا ہے۔ خالص دو طرفہ ریاستوں کے درمیان اس قسم کی تبدیلیوں کو بہت پہلے نمایاں کیا گیا تھا اور ان کی ایک ظاہری نظریاتی ساخت ہے۔ تاہم، یہ پتہ چلتا ہے کہ عام مکمل طور پر الجھی ہوئی خالص کثیر الجہتی ریاستیں LOCC کے تحت کسی بھی غیر مساوی مکمل طور پر الجھی ہوئی ریاست سے حاصل نہیں کی جا سکتی ہیں اور نہ ہی اس میں تبدیل ہو سکتی ہیں۔ اس پراپرٹی کے ساتھ ریاستوں کو الگ تھلگ کہا جاتا ہے۔ بہر حال، کثیر الجہتی ریاستوں کو خاندانوں میں درجہ بندی کیا جاتا ہے، نام نہاد SLOCC کلاسز، جو بہت مختلف خصوصیات کی حامل ہیں۔ اس طرح، مندرجہ بالا نتیجہ مخصوص SLOCC کلاسوں کے وجود کو منع نہیں کرتا جو تنہائی سے پاک ہیں، اور اس وجہ سے، LOCC کنورٹیبلٹی کے حوالے سے ایک بھرپور ڈھانچہ ظاہر کرتا ہے۔ درحقیقت، یہ معلوم ہے کہ مشہور $n$-qubit GHZ اور W ریاستیں ایسی کلاسوں کی خاص مثالیں دیتی ہیں اور اس کام میں، ہم اس سوال کی عمومی طور پر تحقیق کرتے ہیں۔ ہمارے اہم نتائج میں سے ایک یہ ظاہر کرنا ہے کہ 3-کوٹریٹ مکمل طور پر متضاد حالت کی SLOCC کلاس بھی تنہائی سے پاک ہے۔ درحقیقت، اس کلاس کی تمام ریاستوں کو LOCC پروٹوکول کے ذریعے کلاسیکی کمیونیکیشن کے صرف ایک دور (جیسا کہ GHZ اور W کیسز میں) کے ذریعے غیر مساوی ریاستوں میں تبدیل کیا جا سکتا ہے۔ اس طرح، ہم اس پر غور کرتے ہیں کہ آیا اس پراپرٹی کے ساتھ دوسری کلاسیں بھی ہیں اور ہمیں منفی جوابات کا ایک بڑا مجموعہ ملتا ہے۔ درحقیقت، ہم کمزور تنہائی کو ثابت کرتے ہیں (یعنی ایسی ریاستیں جو محدود راؤنڈ LOCC کے ساتھ حاصل نہیں کی جا سکتی ہیں اور نہ ہی ایک راؤنڈ LOCC کے ذریعے تبدیل کی جا سکتی ہیں) بہت عام کلاسوں کے لیے، بشمول تمام SLOCC فیملیز جن میں کمپیکٹ سٹیبلائزرز ہیں اور بہت سے نان کمپیکٹ سٹیبلائزرز کے ساتھ، جیسے $ngeq4$ کے لیے $n$-qunit مکمل طور پر متضاد حالتوں کے مطابق کلاسز۔ آخر میں، خاندان میں پائی جانے والی خوشگوار خصوصیت کو دیکھتے ہوئے جو 3-کوٹریٹ مکمل طور پر متضاد حالت سے مطابقت رکھتا ہے، ہم LOCC کی طرف سے پیدا کردہ ڈھانچے اور اس طبقے کے اندر الجھنے والی خصوصیات کو مزید تفصیل سے تلاش کرتے ہیں۔
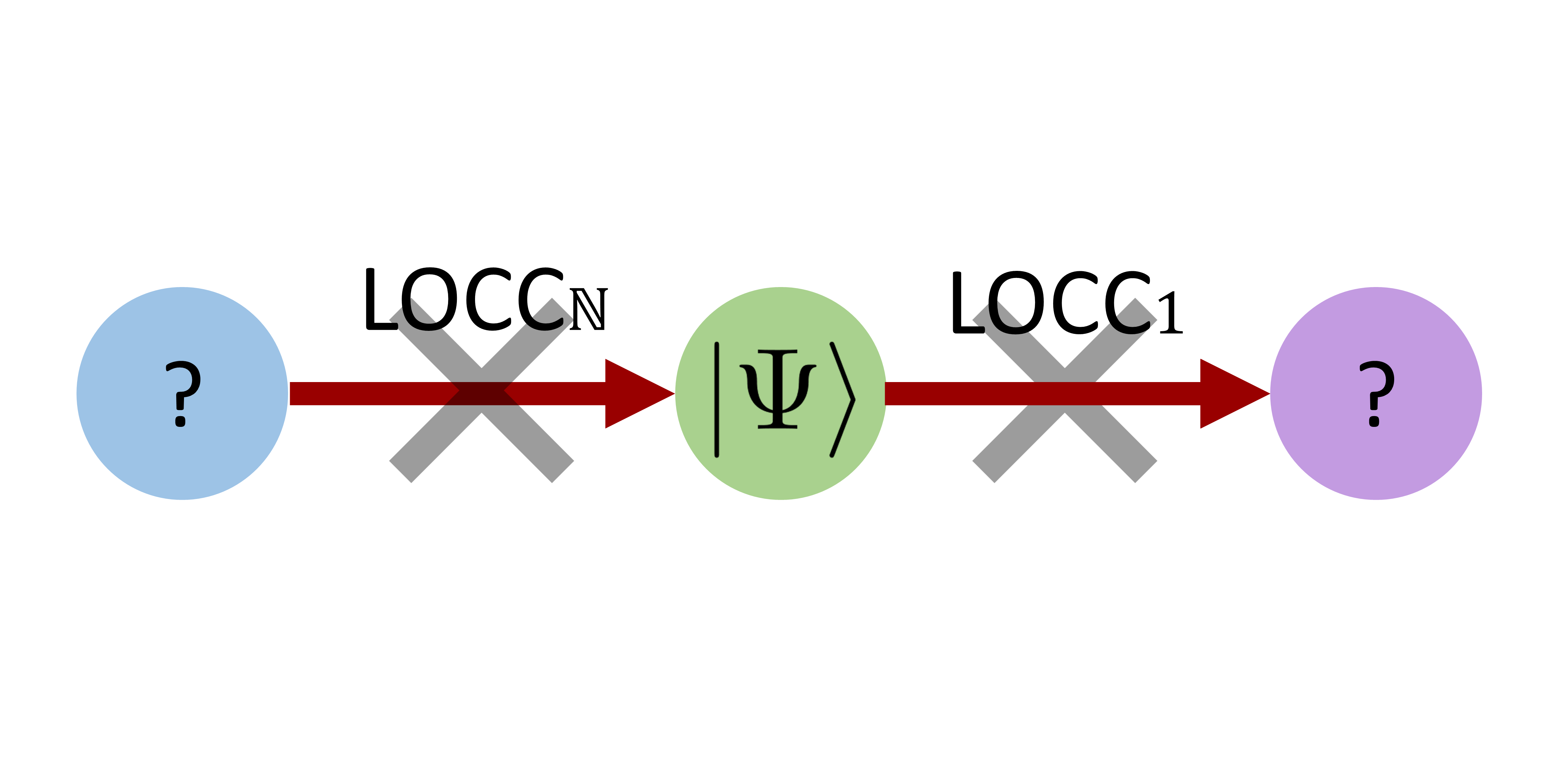
نمایاں تصویر: کمزور تنہائی والی ریاستیں، جو اس مطالعے میں ظاہر ہونے والا ایک بڑا تصور ہے، وہ ریاستیں ہیں جو کسی بھی دوسری مقامی-یونیتری (LU) سے مساوی ریاست سے کسی بھی محدود راؤنڈ LOCC پروٹوکول کے ساتھ تبدیل نہیں ہوسکتی ہیں اور نہ ہی کسی دوسرے LU- میں تبدیل ہوسکتی ہیں۔ کسی بھی سنگل راؤنڈ LOCC پروٹوکول کے ساتھ غیر مساوی حالت۔
مقبول خلاصہ
ابھی تک، ریاستوں کی صرف دو کلاسیں [GHZ اور W ریاستوں کی stochastic LOCC (SLOCC) کلاسز] میں کوئی الگ تھلگ ریاستیں (آئسولیشن فری) نہیں دکھائی گئی ہیں۔ یہاں، ہم ایک نئی تنہائی سے پاک کلاس دریافت کرتے ہیں، جس میں 3-قوت مکمل طور پر متضاد حالت ہوتی ہے، جس میں کچھ دلچسپ الجھنوں کی خصوصیات ہوتی ہیں۔ مزید برآں، ہمیں شواہد ملے ہیں کہ مکمل طور پر الجھی ہوئی خالص ریاستوں کی بہت سی دوسری کلاسیں الگ تھلگ حالتوں پر مشتمل ہیں۔
► BibTeX ڈیٹا
► حوالہ جات
ہے [1] اے کے ایکرٹ، فز۔ Rev. Lett. 67، 661 (1991)۔
https:///doi.org/10.1103/PhysRevLett.67.661
ہے [2] D. Gottesman, Stabilizer Codes and Quantum Error Correction, Ph.D. مقالہ، کیلیفورنیا انسٹی ٹیوٹ آف ٹیکنالوجی، 1997۔
https:///doi.org/10.48550/arXiv.quant-ph/9705052
arXiv:quant-ph/9705052
ہے [3] M. ہلیری، V. Bužek، اور A. Berthiaume، Phys. Rev. A 59، 1829 (1999)۔
https:///doi.org/10.1103/PhysRevA.59.1829
ہے [4] R. Raussendorf اور HJ Briegel، Phys. Rev. Lett. 86، 5188 (2001)۔
https:///doi.org/10.1103/PhysRevLett.86.5188
ہے [5] V. Giovannetti, S. Lloyd, and L. Maccone, Science 306, 1330 (2004).
https://doi.org/10.1126/science.1104149
ہے [6] M. Ben-Or اور A. Hassidim، فاسٹ کوانٹم بازنطینی معاہدہ، تھیوری آف کمپیوٹنگ پر سینتیسویں سالانہ ACM سمپوزیم کی کارروائی میں، STOC '05 (ایسوسی ایشن فار کمپیوٹنگ مشینری، نیویارک، NY، USA، 2005) صفحہ۔ 481–485۔
https://doi.org/10.1145/1060590.1060662
ہے [7] JI Cirac, D. Pérez-García, N. Schuch, and F. Verstraete, Rev. Mod. طبیعیات 93، 045003 (2021)۔
https:///doi.org/10.1103/RevModPhys.93.045003
ہے [8] R. Horodecki, P. Horodecki, M. Horodecki اور K. Horodecki, Rev. Mod. طبیعیات 81، 865 (2009)۔
https:///doi.org/10.1103/RevModPhys.81.865
ہے [9] E. Chitambar اور G. Gour, Rev. Mod. طبیعیات 91، 025001 (2019)۔
https:///doi.org/10.1103/RevModPhys.91.025001
ہے [10] ایم اے نیلسن، فز۔ Rev. Lett. 83، 436 (1999)۔
https:///doi.org/10.1103/PhysRevLett.83.436
ہے [11] W. Dür, G. Vidal, and JI Cirac, Phys. Rev. A 62، 062314 (2000)۔
https:///doi.org/10.1103/PhysRevA.62.062314
ہے [12] F. Verstraete, J. Dehaene, B. De Moor, and H. Verschelde, Phys. Rev. A 65, 052112 (2002)۔
https:///doi.org/10.1103/PhysRevA.65.052112
ہے [13] نوٹ کریں کہ Ref. 4qubitSLOCC 9-qubit ریاستوں کے 4 خاندان فراہم کرتا ہے لیکن ان میں سے کچھ خاندان غیر مساوی SLOCC کلاسوں کی لامحدود تعداد کے مجموعے ہیں (یہ بھی دیکھیں، مثال کے طور پر، Ref. GourBook میں باب 14)۔
ہے [14] جی گور، کوانٹم ورلڈ کے وسائل۔ arXiv:2402.05474v1 [quant-ph] (2024)۔
https://doi.org/10.48550/arXiv.2402.05474
arXiv:2402.05474v1
ہے [15] جی گور اور این آر والاچ، نیو جے فز۔ 13 073013 (2011)۔
https://doi.org/10.1088/1367-2630/13/7/073013
ہے [16] M. Hebenstreit, M. Englbrecht, C. Spee, JI de Vicente, and B. Kraus, New J. Phys. 23، 033046 (2021)۔
https://doi.org/10.1088/1367-2630/abe60c
ہے [17] C. Spee, JI de Vicente, D. Sauerwein, and B. Kraus, Phys. Rev. Lett. 118، 040503 (2017)۔
https:///doi.org/10.1103/PhysRevLett.118.040503
ہے [18] JI de Vicente, C. Spee, D. Sauerwein, and B. Kraus, Phys. Rev. A 95, 012323 (2017)۔
https:///doi.org/10.1103/PhysRevA.95.012323
ہے [19] JI de Vicente, C. Spee, and B. Kraus, Phys. Rev. Lett. 111، 110502 (2013)۔
https:///doi.org/10.1103/PhysRevLett.111.110502
ہے [20] G. Gour, B. Kraus, and NR Wallach, J. Math. طبیعیات 58، 092204 (2017)۔
https://doi.org/10.1063/1.5003015
ہے [21] D. Sauerwein, NR Wallach, G. Gour, and B. Kraus, Phys. Rev. X 8, 031020 (2018)۔
https:///doi.org/10.1103/PhysRevX.8.031020
ہے [22] S. Turgut, Y. Gül, اور NK Pak, Phys. Rev. A 81، 012317 (2010)۔
https:///doi.org/10.1103/PhysRevA.81.012317
ہے [23] S. Kıntaş اور S. Turgut, J. Math. طبیعیات 51، 092202 (2010)۔
https://doi.org/10.1063/1.3481573
ہے [24] C. سپی، JI de Vicente، اور B. Kraus، J. Math. طبیعات 57، 052201 (2016)۔
https://doi.org/10.1063/1.4946895
ہے [25] M. Hebenstreit, C. Spee, and B. Kraus, Phys. Rev. A 93، 012339 (2016)۔
https:///doi.org/10.1103/PhysRevA.93.012339
ہے [26] M. Englbrecht اور B. Kraus، Phys. Rev. A 101, 062302 (2020)۔
https:///doi.org/10.1103/PhysRevA.101.062302
ہے [27] D. Sauerwein, A. Molnar, JI Cirac, اور B. Kraus, Phys. Rev. Lett. 123، 170504 (2019)۔
https:///doi.org/10.1103/PhysRevLett.123.170504
ہے [28] M. Hebenstreit, D. Sauerwein, A. Molnar, JI Cirac, and B. Kraus, Phys. Rev. A 105, 032424 (2022)۔
https:///doi.org/10.1103/PhysRevA.105.032424
ہے [29] M. Hebenstreit, C. Spee, NKH Li, B. Kraus, JI de Vicente, Phys. Rev. A 105, 032458 (2022)۔
https:///doi.org/10.1103/PhysRevA.105.032458
ہے [30] H. Yamasaki, A. Soeda, and M. Murao, Phys. Rev. A 96, 032330 (2017)۔
https:///doi.org/10.1103/PhysRevA.96.032330
ہے [31] C. Spee and T. Kraft, arXiv:2105.01090 [quant-ph] (2021)۔
https://doi.org/10.48550/arXiv.2105.01090
آر ایکس سی: 2105.01090
ہے [32] W. Jian, Z. Quan, اور T. Chao-Jing, Commun. تھیور طبیعیات 48، 637 (2007)۔
https://doi.org/10.1088/0253-6102/48/4/013
ہے [33] W. Dür، طبیعیات. Rev. A 63, 020303(R) (2001)۔
https:///doi.org/10.1103/PhysRevA.63.020303
ہے [34] اے کابیلو، فز۔ Rev. Lett. 89، 100402 (2002)۔
https:///doi.org/10.1103/PhysRevLett.89.100402
ہے [35] M. Fitzi، N. Gisin، اور U. Maurer، Phys. Rev. Lett. 87، 217901 (2001)۔
https:///doi.org/10.1103/PhysRevLett.87.217901
ہے [36] MT Quintino, Q. Dong, A. Shimbo, A. Soeda, and M. Murao, Phys. Rev. Lett. 123، 210502 (2019)۔
https:///doi.org/10.1103/PhysRevLett.123.210502
ہے [37] S. Yoshida, A. Soeda, and M. Murao, Quantum 7, 957 (2023)۔
https://doi.org/10.22331/q-2023-03-20-957
ہے [38] H.-K لو اور ایس پوپیسکو، فز۔ Rev. A 63، 022301 (2001)۔
https:///doi.org/10.1103/PhysRevA.63.022301
ہے [39] دھیان دیں کہ تبادلوں کی مثالیں جو یک طرفہ پروٹوکول کو جوڑ کر حاصل نہیں کی جا سکتی ہیں، یہ ثابت نہیں کرتی ہیں۔ اس کی وجہ یہ ہے کہ آؤٹ پٹ سٹیٹ خود بخود کمزور طور پر الگ تھلگ نہیں ہوتی ہے (یہ لازمی طور پر قابل رسائی ہونا چاہئے) اور ان پٹ سٹیٹ ایک راؤنڈ کسی مختلف حالت میں تبدیل ہو سکتی ہے۔
ہے [40] J. Eisert اور H. J. Briegel، Phys. Rev. A 64, 022306 (2001)۔
https:///doi.org/10.1103/PhysRevA.64.022306
ہے [41] اس کی وجہ یہ ہے کہ کوئی بھی میٹرکس $bigotimes_{j=1}^n X^{(j)}bigotimes_{i=1}^n GL(d_i,mathbb{C})$ میں $frac{ کے درمیان ٹینسر پروڈکٹ کے برابر ہے۔ X^{(j)}}{det(X^{(j)})^{1/d_j}}SL(d_j,mathbb{C})$ میں کسی بھی $n-1$ انڈیکسز $j$ اور $prod_{jneq k}det(X^{(j)})^{1/d_j} X^{(k)}$ بقیہ انڈیکس $k$ کے لیے۔
LOCCRef1″>[42] CH Bennett, DP DiVincenzo, CA Fuchs, T. Mor, E. Rains, PW Shor, JA Smolin, and WK Wootters, Phys. Rev. A 59, 1070 (1999)۔
https:///doi.org/10.1103/PhysRevA.59.1070
ہے [43] MJ Donald, M. Horodecki, and O. Rudolph, J. Math. طبیعیات 43، 4252 (2002)۔
https://doi.org/10.1063/1.1495917
ہے [44] ای چتامبر، طبعیات۔ Rev. Lett. 107، 190502 (2011)۔
https:///doi.org/10.1103/PhysRevLett.107.190502
ہے [45] E. Chitambar, D. Leung, L. Mančinska, M. Ozols, and A. Winter, Commun. ریاضی طبیعیات 328، 303 (2014)، اور اس میں حوالہ جات۔
https://doi.org/10.1007/s00220-014-1953-9
ہے [46] ہم کہتے ہیں کہ ایک میٹرکس $X$ کسی دوسرے میٹرکس $A$ کے ساتھ ارد گرد سفر کرتا ہے اگر اور صرف اس صورت میں جب $X^dagger AX= kApropto A$ کچھ $kinmathbb{C}$ کے لیے۔
ہے [47] F. Verstraete, J. Dehaene, and B. De Moor, Phys. Rev. A 65, 032308 (2002)۔
https:///doi.org/10.1103/PhysRevA.65.032308
ہے [48] مزید واضح طور پر، $P$ کو $P=|vranglelangle v|+{1}$ کے طور پر منتخب کیا جا سکتا ہے، جہاں $|vrangle inmathbb{C}^d$ کسی بھی $U_iinmathcal{F}$ کا ایک ایجین ویکٹر نہیں ہے۔ اس طرح کا ویکٹر ہمیشہ موجود رہتا ہے کیونکہ $mathbb{C}$ پر کوئی محدود جہتی ویکٹر کی جگہ مناسب ذیلی جگہوں کا ایک محدود اتحاد نہیں ہے (مثال کے طور پر، Ref. VecSpaceNOTfiniteUnion دیکھیں)۔
ہے [49] A. کھرے، لکیری الجبرا اور اس کے اطلاقات 431(9)، 1681-1686 (2009)۔
https://doi.org/10.1016/j.laa.2009.06.001
ہے [50] یہ آسانی سے مندرجہ ذیل طور پر دیکھا جا سکتا ہے. سب سے پہلے، ریاست کی ہم آہنگی کی وجہ سے، یہ دیکھنا آسان ہے کہ SLOCC کلاس میں کوئی بھی ریاست $sqrt{G_1}otimesqrt{D_2}otimes {1}|A_3rangle $ کے برابر LU ہے [دیکھیں Eq۔ (29)] جہاں $G_1>0$ اور $D_2=diag(alpha_2,beta_2,1) >0$۔ مزید برآں، $U^{otimes3}$$|A_3rangle $ کا استعمال کرتے ہوئے، جہاں $U=diag(e^{itheta},e^{ivarphi},e^{-i(theta+varphi)})$ کے ساتھ $theta=-frac{arg(gamma_1)+arg(delta_1)}{3}$, $varphi=frac{2arg(gamma_1)-arg(delta_1)}{3}$, $gamma_1=(G_1)_{12 }$ اور $delta_1=(G_1)_{13}$، اوپر کی طرح کی حالت کی طرف لے جاتا ہے، لیکن $G_1$ کی جگہ $U G_1 U^dagger$، جس کے اندراجات $(1,2)$ ہیں اور $(1,3)$ صفر سے بڑے یا برابر ہیں۔ لہذا، ریاستیں (LU تک) 8 پیرامیٹرز سے پیرامیٹرائزڈ ہیں۔
ہے [51] JI de Vicente, T. Carle, C. Streitberger, and B. Kraus, Phys. Rev. Lett. 108، 060501 (2012)۔
https:///doi.org/10.1103/PhysRevLett.108.060501
ہے [52] M. Hebenstreit, B. Kraus, L. Ostermann, and H. Ritsch, Phys. Rev. Lett. 118، 143602 (2017)۔
https:///doi.org/10.1103/PhysRevLett.118.143602
ہے [53] نوٹ کریں کہ ہم یہاں $alpha_2$ اور $beta_1$ کے آرڈر کا تبادلہ کرتے ہیں اس اشارے کے برخلاف جو ہم مشاہدہ 11 میں $M_{A_3}$ میں ریاستوں کو ظاہر کرنے کے لیے استعمال کرتے ہیں۔
ہے [54] ایف برنارڈز اور او گوہنے، جے میتھ۔ طبیعیات 65، 012201 (2024)۔
https://doi.org/10.1063/5.0159105
ہے [55] جو دلیل ہم یہاں یہ ظاہر کرنے کے لیے استعمال کرتے ہیں کہ $Botimes B^{-1}otimes {1}^{otimes n-2}inmathcal{S}_{|A_nrangle }$ وہی دلیل ہے جو Ref. MigdalSymm (Sec. II) یہ ثابت کرنے کے لیے کہ permutation-symmetric ریاستوں میں $Botimes B^{-1}otimes {1}^{otimes n-2}$ کی ہم آہنگی ہوتی ہے۔
ہے [56] P. Migdał, J. Rodriguez-Laguna, اور M. Lewenstein, Phys. Rev. A 88, 012335 (2013)۔
https:///doi.org/10.1103/PhysRevA.88.012335
ہے [57] حوالہ جات کا صفحہ 8 دیکھیں۔ Zariski اس حقیقت کے لیے بند ہوا کہ $mathbb{C}^d$ پر Zariski کی بندش کا مطلب $mathbb{C}^d$ پر یوکلیڈین بندش ہے۔
ہے [58] KE سمتھ، L. Kahanpää، P. Kekäläinen، اور W. Traves، الجبری جیومیٹری کی دعوت، اسپرنگر نیویارک، 2000۔
https://doi.org/10.1007/978-1-4757-4497-2
ہے [59] پی ایم فٹز پیٹرک، ایڈوانسڈ کیلکولس (دوسرا ایڈیشن)، تھامسن بروکس/کول، 2۔
ہے [60] یہ دیکھنا آسان ہے کہ بولزانو-ویئرسٹراس تھیوریم $mathbb{C}^d$ میں پابند ترتیبوں پر بھی لاگو ہوتا ہے اور انہیں $mathbb{R}^{2d}$ میں ترتیب کے طور پر دیکھ کر۔
ہے [61] J. Mickelsson, J. Niederle, Commun. ریاضی طبیعیات 16، 191–206 (1970)۔
https://doi.org/10.1007/BF01646787
ہے [62] سمجھی جانے والی حالت پھر ابتدائی حالت کے LU کے مساوی ہو سکتی ہے۔
ہے [63] نوٹ کریں کہ اگر $x_1^{(lambda)}=0$ اور $x_2^{(lambda)}neq0$ کے ساتھ ایک مستقل حالت موجود ہے جبکہ $theta$ $pi$ کا ایک غیر معقول ضرب ہے، تو مساوات کا نظام ہے متضاد
ہے [64] ہم Eq حاصل کرتے ہیں۔ 20 ہر ایک مساوات.
=5″>[65] اگرچہ کمزور تنہائی کا وجود $(ngeq5)$-qudit غیر غیر معمولی ہم آہنگی (غیر ES) ریاستوں کی SLOCC کلاسوں کے لیے ثابت کیا گیا تھا، جو کہ $S^{otimes n}$ کی شکل کی صرف ہم آہنگی کے ساتھ permutation-symmetric ریاستیں ہیں۔ , Ref کے Lemma 4 میں. OurSymmPaper، ثبوت کسی بھی $n$-qudit SLOCC کلاس پر بھی لاگو ہوتا ہے جس کی حالت صرف $S^{otimes n}$ سے $ngeq5$ تک مستحکم ہوتی ہے۔
ہے [66] جے جے ساکورائی۔ جدید کوانٹم میکانکس (نظر ثانی شدہ ایڈیشن)۔ ایڈیسن ویزلی، 1993۔
ہے [67] $E_p$ اور $|e_prangle $ کے لیے perturbation سیریز کے آپس میں ملنے کی ضمانت ہے کیونکہ میٹرکس $H_0 + epsilon V(epsilon)$ ہرمیٹیئن اور تجزیاتی ہے (یعنی ہر میٹرکس اندراج تجزیاتی ہے) $epsilon=0$ کے پڑوس میں جہاں $epsiloninmathbb{R}$ اور Rellich's Theorem Rellich,FriedlandBook کے ذریعے، eigenvectors کی تمام eigenvalues اور entries کو $epsilon=0$ کے پڑوس میں بھی تجزیاتی ہونا چاہیے۔
ہے [68] F. Rellich، Eigenvalue Problems کی Perturbation Theory، Gordon & Breach، نیویارک، 1969۔
ہے [69] S. Friedland, Matrices: Algebra, Analysis and Applications, World Scientific, 2015.
ہے [70] چونکہ eigenvalue $E_p$ کی perturbation سیریز $epsilon$ میں بدل جاتی ہے، اس لیے کوئی $epsilon$ کو اتنا چھوٹا منتخب کر سکتا ہے کہ $mathcal{O}(epsilon^2)$ اصطلاحات کے مجموعہ کی مطلق قدر $ سے سختی سے کم ہو۔ frac{1}{2}(frac{1}{r}-1)$ کے لیے $E_0$ اور $frac{1}{2r^{p-1}}(frac{1}{r}-1)$ ، جو کہ $(p-1)$-th اور $p$-th کے غیر متزلزل eigenvalues کے درمیان آدھا فاصلہ ہے، $E_p$ کے لیے جہاں $pin{1,ldots,d-1}$ اور $0
ہے [71] چونکہ eigenvector $|e_prangle $ کی perturbation سیریز $epsilon$ میں بدل جاتی ہے، اس لیے کوئی $epsilon$ کو اتنا چھوٹا منتخب کر سکتا ہے کہ $mathcal{O}(epsilon^2)$ کی اصطلاحات کے مجموعے کی مطلق قدر $langle0| e_prangle$ $|e_1rangle $ اور $|frac{epsilonsqrt{r}^{p}}{(0-r^p)(1-omega^{-p})}|$ کے لیے 1 سے سختی سے چھوٹا ہے |e_prangle $ جہاں $pin{1,ldots,d-1}$، ${E_p}$ کو غیر ڈیجینریٹ فوٹ نوٹ:پرٹ رکھتے ہوئے۔
ہے [72] مندرجہ ذیل کو دیکھنا آسان ہے: اگر $Sin SL(d,mathbb{C})$ دو $dtimes d$ مثبت قطعی اخترن میٹرکس $Lambda$ اور $D$ کے ساتھ ارد گرد سفر کرتا ہے جیسے $Lambdanotpropto D$, $S $ بلاک میٹرکس کا براہ راست مجموعہ ہونا چاہیے جو $Lambda^{-1}D$ کے (ڈیجنریٹ) eigenspaces پر کام کرتا ہے۔ مزید برآں، $S$ میں ہر بلاک کے لیے جس کی حد $Lambda$ یا $D$ کی واحد eigenvalue کی (degenerate) eigen اسپیس کے اندر ہوتی ہے، یہ بلاک وحدانی ہے۔
ہے [73] Eq کو ضرب کرتے وقت 1 {D}otimes {3}$، اصطلاح $g^daggersum_q N_q^dagger N_q g|A_1rangle =1$ کیونکہ تمام $N_qinmathcal{N}_{gPsi_s}$ $N_q g|A_3rangle =0$ کی تعریف کے مطابق۔
ہے [74] متبادل طور پر، کوئی بھی یہ دکھا کر دیکھ سکتا ہے کہ $|A_3rangle $ مشاہدہ 11 میں تمام MES امیدواروں میں واحد ریاست ہے جس میں تمام 3 دو طرفہ تقسیم کے لیے مکمل طور پر مخلوط واحد قوٹریٹ کم کثافت میٹرکس ہے۔ نیلسن کے تھیوریم نیلسن کو تمام 3 دو حصوں پر لاگو کرنا ثابت کرتا ہے کہ $|A_3rangle $ واقعی LOCC کے قابل نہیں ہے۔
ہے [75] اوپر کی تیاری کا طریقہ کار $ .
کی طرف سے حوالہ دیا گیا
[1] Moisés Bermejo Morán، Alejandro Pozas-Kerstjens، اور Felix Huber، "Overlapping Measurements کے ساتھ بیل عدم مساوات"، جسمانی جائزہ کے خطوط 131 8, 080201 (2023).
[2] انوبھو کمار سریواستو، Guillem Müller-Rigat، Maciej Lewenstein، اور Grzegorz Rajchel-Mieldzioć، "متعدد جسمانی نظاموں میں کوانٹم الجھن کا تعارف"، آر ایکس سی: 2402.09523, (2024).
مذکورہ بالا اقتباسات سے ہیں۔ SAO/NASA ADS (آخری بار کامیابی کے ساتھ 2024-03-02 02:41:23)۔ فہرست نامکمل ہو سکتی ہے کیونکہ تمام ناشرین مناسب اور مکمل حوالہ ڈیٹا فراہم نہیں کرتے ہیں۔
On Crossref کی طرف سے پیش خدمت کاموں کے حوالے سے کوئی ڈیٹا نہیں ملا (آخری کوشش 2024-03-02 02:41:21)۔
یہ مقالہ کوانٹم میں کے تحت شائع کیا گیا ہے۔ Creative Commons انتساب 4.0 انٹرنیشنل (CC BY 4.0) لائسنس کاپی رائٹ اصل کاپی رائٹ ہولڈرز جیسے مصنفین یا ان کے اداروں کے پاس رہتا ہے۔
- SEO سے چلنے والا مواد اور PR کی تقسیم۔ آج ہی بڑھا دیں۔
- پلیٹو ڈیٹا ڈاٹ نیٹ ورک ورٹیکل جنریٹو اے آئی۔ اپنے آپ کو بااختیار بنائیں۔ یہاں تک رسائی حاصل کریں۔
- پلیٹوآئ اسٹریم۔ ویب 3 انٹیلی جنس۔ علم میں اضافہ۔ یہاں تک رسائی حاصل کریں۔
- پلیٹو ای ایس جی۔ کاربن، کلین ٹیک، توانائی ، ماحولیات، شمسی، ویسٹ مینجمنٹ یہاں تک رسائی حاصل کریں۔
- پلیٹو ہیلتھ۔ بائیوٹیک اینڈ کلینیکل ٹرائلز انٹیلی جنس۔ یہاں تک رسائی حاصل کریں۔
- ماخذ: https://quantum-journal.org/papers/q-2024-02-29-1270/
- : ہے
- : ہے
- : نہیں
- :کہاں
- ][p
- $UP
- 001
- 06
- 1
- 10
- 11
- 118
- 12
- 13
- 14
- 15٪
- 16
- 17
- 19
- 1999
- 20
- 2000
- 2001
- 2005
- 2006
- 2009
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2018
- 2019
- 2020
- 2021
- 2022
- 2023
- 2024
- 22
- 23
- 24
- 25
- 26٪
- 27
- 28
- 29
- 2nd
- 30
- 31
- 32
- 33
- 35٪
- 36
- 39
- 40
- 41
- 43
- 49
- 50
- 51
- 54
- 58
- 60
- 65
- 66
- 67
- 7
- 70
- 72
- 75
- 8
- 87
- 89
- 9
- 91
- a
- اوپر
- مطلق
- خلاصہ
- تک رسائی حاصل
- حاصل کیا
- ACM
- ایکٹ
- اصل میں
- ایڈسن
- اس کے علاوہ
- پتہ
- اعلی درجے کی
- فائدہ
- وابستگیاں
- پہلے
- معاہدہ
- مقصد ہے
- تمام
- تقریبا
- بھی
- اگرچہ
- ہمیشہ
- کے درمیان
- an
- تجزیہ
- تجزیاتی
- اور
- سالانہ
- ایک اور
- جواب
- کوئی بھی
- ظاہر ہوتا ہے
- ایپلی کیشنز
- لاگو ہوتا ہے
- درخواست دینا
- کیا
- دلیل
- AS
- مدد
- ایسوسی ایشن
- At
- کرنے کی کوشش
- مصنف
- مصنفین
- خود کار طریقے سے
- BE
- کیونکہ
- ہو جاتا ہے
- رہا
- بیل
- کے درمیان
- بلاک
- دونوں
- دونوں اطراف
- خلاف ورزی
- توڑ
- لیکن
- by
- کیلی فورنیا
- کر سکتے ہیں
- امیدواروں
- نہیں کر سکتے ہیں
- کارلوس
- کیا ہوا
- مقدمات
- جشن منایا
- کچھ
- باب
- خصوصیات
- میں سے انتخاب کریں
- منتخب کیا
- طبقے
- کلاس
- درجہ بندی
- بندش
- کوڈ
- مجموعے
- کالم
- تبصرہ
- عمومی
- مواصلات
- کمپیکٹ
- ہم آہنگ
- مکمل
- مکمل طور پر
- کمپیوٹنگ
- تصور
- شرط
- غور کریں
- سمجھا
- پر مشتمل ہے
- تقارب
- تبادلوں
- تبدیل
- تبدیل
- کاپی رائٹ
- Cornelia
- باہمی تعلق۔
- اسی کے مطابق
- کاؤنٹر پارٹ
- ہم منصبوں
- اہم
- اعداد و شمار
- de
- تعریف
- بیان
- تفصیل
- مختلف
- طول و عرض
- براہ راست
- دریافت
- بات چیت
- دکھائیں
- فاصلے
- do
- کرتا
- ڈونالڈ
- ڈونگ
- دو
- e
- ہر ایک
- آسانی سے
- آسان
- ed
- ایڈیشن
- کارکردگی
- کافی
- داخلہ
- اندراج
- برابر
- مساوات
- مساوی
- خرابی
- ہر کوئی
- ثبوت
- مثال کے طور پر
- ایکسچینج
- وجود
- موجود ہے
- تلاش
- حقیقت یہ ہے
- عنصر
- خاندانوں
- خاندان
- دور
- دلچسپ
- فاسٹ
- نمایاں کریں
- فروری
- آخر
- مل
- پہلا
- Fitzpatrick
- کے بعد
- مندرجہ ذیل ہے
- کے لئے
- فارم
- ملا
- مفت
- سے
- مکمل طور پر
- جنرل
- دے دو
- دی
- گورڈن
- بات کی ضمانت
- نصف
- کنٹرول
- ہارورڈ
- ہے
- لہذا
- یہاں
- ہولڈرز
- ہانگ
- تاہم
- HTTPS
- i
- شناخت
- کی نشاندہی
- if
- ii
- III
- تصویر
- in
- سمیت
- اضافہ
- یقینا
- انڈکس
- Indices
- اسماتایں
- لامتناہی
- معلومات
- ابتدائی
- ان پٹ
- انسٹی ٹیوٹ
- اداروں
- دلچسپ
- بین الاقوامی سطح پر
- میں
- تعارف
- کی تحقیقات
- دعوت نامہ
- غیر معقول
- الگ الگ
- تنہائی
- IT
- میں
- جاوا سکرپٹ
- جرنل
- صرف
- صرف ایک
- رکھتے ہوئے
- جانا جاتا ہے
- کمر
- بڑے
- بڑے
- آخری
- لیڈز
- چھوڑ دو
- لیما
- کم
- Li
- لائسنس
- جھوٹ ہے
- لکیری
- لسٹ
- مقامی
- لانگ
- LP
- مشینری
- مین
- اہم
- ہیرا پھیری
- بہت سے
- مارٹن
- ریاضی
- میٹرکس
- زیادہ سے زیادہ چوڑائی
- مئی..
- MBC
- پیمائش
- میکینکس
- شاید
- مخلوط
- جدید
- مہینہ
- زیادہ
- اس کے علاوہ
- ایک سے زیادہ
- ضرب لگانا
- ضروری
- ضرورت ہے
- منفی
- پھر بھی
- نئی
- NY
- اگلے
- نہیں
- براہ مہربانی نوٹ کریں
- نوٹس..
- تعداد
- NY
- جائزہ
- حاصل
- حاصل کی
- of
- on
- ایک
- صرف
- کھول
- آپریشنز
- مخالفت کی
- or
- حکم
- اصل
- دیگر
- ہمارے
- باہر
- پیداوار
- پر
- صفحات
- کاغذ.
- پیرامیٹرز
- خاص طور پر
- جماعتوں
- طبعیات
- پلاٹا
- افلاطون ڈیٹا انٹیلی جنس
- پلیٹو ڈیٹا
- ادا کرتا ہے
- مثبت
- قبضہ کرو
- ممکن
- ٹھیک ہے
- تیاری
- مسائل
- طریقہ کار
- کارروائییں
- پروسیسنگ
- مصنوعات
- ثبوت
- مناسب
- خصوصیات
- جائیداد
- پروٹوکول
- پروٹوکول
- ثابت کریں
- ثابت
- ثابت ہوتا ہے
- فراہم
- فراہم کرتا ہے
- فراہم کرنے
- شائع
- پبلیشر
- پبلشرز
- پاک
- کوانٹم
- کوانٹم الجھن
- کوانٹم غلطی کی اصلاح
- کوانٹم معلومات
- کوانٹم میکینکس
- سوال
- R
- رینج
- کم
- حوالہ جات
- کہا جاتا ہے
- کے بارے میں
- باقی
- باقی
- کی جگہ
- وسائل
- وسائل
- نتیجہ
- نتائج کی نمائش
- انکشاف
- کا جائزہ لینے کے
- امیر
- کردار
- منہاج القرآن
- s
- اسی
- مطمئن
- کا کہنا ہے کہ
- سائنس
- سائنسی
- SEC
- دیکھنا
- بیج
- دیکھا
- سیریز
- مقرر
- شور
- دکھائیں
- ظاہر
- دکھایا گیا
- اطمینان
- بعد
- ایک
- چھوٹے
- چھوٹے
- سمتھ
- کچھ
- خلا
- حالت
- امریکہ
- مضبوط
- ساخت
- مطالعہ
- کامیابی کے ساتھ
- اس طرح
- موزوں
- سمپوزیم
- کے نظام
- سسٹمز
- کاموں
- ٹیکنیکل
- ٹیکنالوجی
- ٹیکنالوجی
- اصطلاح
- شرائط
- سے
- کہ
- ۔
- بلاک
- میٹرکس
- ریاست
- ان
- ان
- تو
- نظریاتی
- نظریہ
- وہاں.
- اس طرح
- لہذا
- اس میں
- یہ
- مقالہ
- اس
- اس طرح
- عنوان
- کرنے کے لئے
- مکمل طور پر
- تبدیلی
- تبدیلی
- تبدیل
- دیتا ہے
- دو
- قسم
- کے تحت
- یونین
- یونیورسٹی
- اپ ڈیٹ
- URL
- امریکا
- استعمال کی شرائط
- استعمال کیا جاتا ہے
- مفید
- کا استعمال کرتے ہوئے
- قیمت
- بہت
- دیکھنے
- حجم
- W
- چاہتے ہیں
- تھا
- طریقوں
- we
- کمزور
- اچھا ہے
- تھے
- جب
- چاہے
- جس
- جبکہ
- پوری
- کس کی
- موسم سرما
- ساتھ
- کے اندر
- کام
- کام کرتا ہے
- دنیا
- X
- سال
- یارک
- زیفیرنیٹ
- صفر