حیرت انگیز کمپیوٹر سائنس کا ثبوت ریاضی دانوں کو دنگ کر دیتا ہے۔

اتوار، 5 فروری کو، Olof Sisask اور Thomas Bloom کو ایک ای میل موصول ہوئی جس میں ان کے شعبے کے سب سے بڑے حل نہ ہونے والے مسئلے پر ایک شاندار پیش رفت تھی۔ زینڈر کیلی، یونیورسٹی آف الینوائے، اربانا-چمپین کے گریجویٹ طالب علم نے سیساسک اور بلوم بھیجے تھے۔ ایک کاغذ جو اس نے لکھا تھا۔ یونیورسٹی آف کیلیفورنیا، لاس اینجلس کے رگھو میکا کے ساتھ۔ کیلی اور میکا دونوں کمپیوٹر سائنس دان تھے، ایک فکری دنیا ان اضافی امتزاجات کے علاوہ جس کا سسسک اور بلوم مطالعہ کرتے ہیں۔

"میرا دماغ ابھی اڑا ہوا تھا۔ جیسے، انتظار کرو، کیا انہوں نے واقعی یہ کیا ہے؟" سٹاک ہوم یونیورسٹی کے لیکچرر سیسسک نے کہا۔ کیلی اور میکا، جو کمبینیٹرکس کے شعبے سے باہر ہیں، نے کہا کہ انہیں عدد کے سیٹ کے سائز پر ایک نئی — اور ڈرامائی طور پر کم — حد ملی ہے جس میں ان میں سے کوئی بھی یکساں فاصلہ نہیں رکھتا ہے (3، 8 اور 13 جیسے مجموعوں کو مسترد کرتے ہوئے یا 101، 201 اور 301)۔

کیلی اور میکا کے دعوے نے پچھلا ریکارڈ توڑ دیا، 2020 میں حاصل ہوا۔ سسسک اور بلوم کے ذریعہ، جو آکسفورڈ یونیورسٹی میں ریسرچ فیلو ہیں۔ آکسفورڈ میں بلوم کے ایک ساتھی بین گرین نے کہا، "بلوم اور سسسک کا کام - بہت مضبوط کام جو کہ تھا - اس نے واقعی یہ تاثر دیا کہ اس میں بہتری لانا بہت مشکل ہے۔" "یہ جہاں تھا وہاں بہت پھنس گیا تھا۔"

اگرچہ بلوم اور سسسک دونوں کے پاس ای میل موصول ہونے کے وقت میں شرکت کے لیے دیگر اہم معاملات تھے — بلوم نے ابھی ایک کتے کو گود لیا تھا، جب کہ سیساسک آگے بڑھنے کے بیچ میں تھا — وہ جلدی سے نئے کاغذ کی تصدیق کے لیے کام کرنے لگے۔

کچھ ہی دنوں میں، بلوم اور سسسک کو یقین ہو گیا کہ نیا ثبوت درست ہے۔ سسسک نے اسے "20 سالوں میں علاقے کا سب سے بڑا نتیجہ" قرار دیا۔ دوسروں کے لیے کیلی اور میکا کے خیالات کی تعریف کرنے کے خواہشمند، انہوں نے مسودہ تیار کیا۔ ایک رپورٹ ریاضی دانوں سے زیادہ واقف کے لحاظ سے ثبوت کی وضاحت کرنا۔

میکا نے کہا کہ کمیونٹی کی طرف سے ردعمل "میرے خیال سے زیادہ مثبت رہا ہے۔ تمام آراء کو دیکھنا حیرت انگیز ہے۔"

طویل پیشرفت

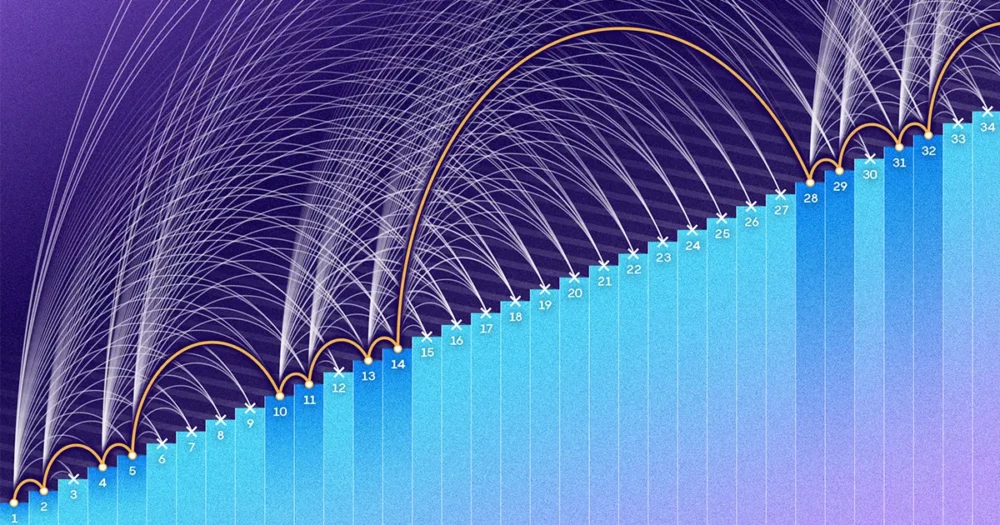
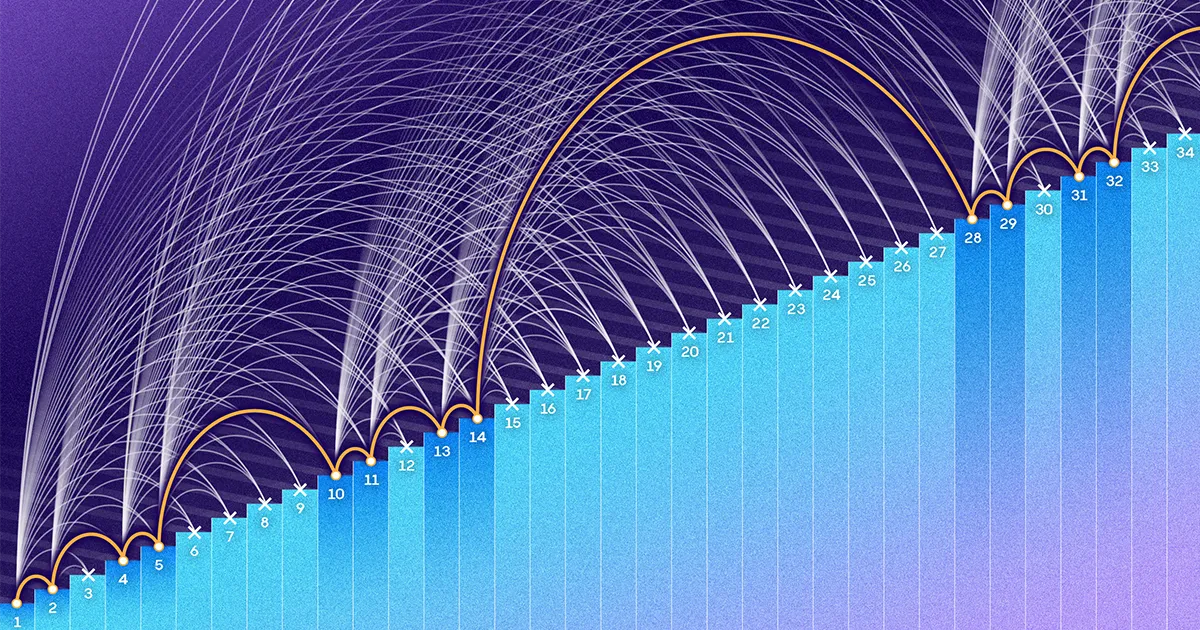
یکساں فاصلہ والے نمبروں کی ترتیب جن سے کیلی اور میکا نے گریز کرنا چاہا انہیں ریاضی کی ترقی کہتے ہیں۔ وہ ہمیشہ کے لیے چل سکتے ہیں یا صرف چند شرائط پر مشتمل ہو سکتے ہیں۔ کیلی اور میکا کی توجہ صرف تین نمبروں پر مشتمل ترقی پر مرکوز تھی، تحقیق کی ایک لائن کے بعد اکثر 1936 کاغذ بذریعہ Paul Erdős اور Paul Turán۔

Erdős اور Turán یہ جاننا چاہتے تھے کہ کسی حد سے کتنے چھوٹے نمبر ہیں۔ N کسی بھی تین مدتی ریاضی کی ترقی کو بنائے بغیر سیٹ میں ڈالا جا سکتا ہے۔ N 1,000، 1 ملین، یا کچھ ناقابل تصور حد تک بڑی تعداد ہو سکتی ہے۔ انہوں نے قیاس کیا کہ N بڑا ہوا، تین مدتی ترقی کے بغیر ایک سیٹ کو ناقابل یقین حد تک ویرل ہونا پڑے گا۔ اس طرح کا سیٹ بنانا جوتوں کو جمع کرنے کے مترادف ہوگا جب کہ اس بات پر اصرار کیا جائے کہ کوئی دو جوڑے ایک ہی رنگ کے نہ ہوں۔ شاید آپ ہمیشہ کے لیے جاری رکھ سکتے ہیں، لیکن جیسے جیسے آپ کا مجموعہ بڑا ہوتا گیا، آپ خود کو اس میں دھیمی اور سست رفتار سے اضافہ کرتے ہوئے پائیں گے۔

میکا نے وضاحت کرتے ہوئے کہا، "کچھ ڈھانچہ ہے جو سیٹ میں پاپ جائے گا، چاہے آپ نے سیٹ کا انتخاب کیسے کیا ہو۔" "آپ کو واقعی اس بات کی ضمانت دینے کے لیے کتنے بڑے سیٹ کی ضرورت ہے کہ آپ کے پاس یہ ڈھانچہ موجود ہے؟"

1946 میں، فیلکس بہرینڈ سیٹ بنانے کا ایک طریقہ ملا 1 اور کے درمیان نمبروں کا N بغیر کسی تین مدتی ترقی کے۔ اس کے طریقہ کار کے نتیجے میں سیٹوں میں اضافہ ہوا N کیا، لیکن درد آہستہ آہستہ. کب N 100,000 ہے، Behrend کے سیٹ میں صرف 171 عناصر ہیں۔ کب N 1 ملین ہے، اس کے سیٹ میں 586 نمبر ہیں - 0.06 اور 1 ملین کے درمیان نمبروں کے 1 فیصد سے بھی کم۔

بہرینڈ کے سیٹ نے ریاضی دانوں کو کام کرنے کے لیے ایک منزل فراہم کی: تین مدتی ترقی کے بغیر سب سے بڑا سیٹ کم از کم بہرینڈ جتنا بڑا ہونا چاہیے۔ 1953 میں کلاؤس روتھ ایک چھت فراہم کی, ایک حد ماضی کو تلاش کرنا جس میں ایک سیٹ میں لازمی طور پر تین مدتی ترقی ہونی چاہیے۔

روتھ نے ایردوس اور ٹوران کے قیاس کو یہ دکھا کر ثابت کیا تھا۔ N بڑا ہو جاتا ہے، تین مدتی ترقی کے بغیر ایک سیٹ 1 اور N کے درمیان نمبروں کا ہمیشہ سے چھوٹا حصہ پر مشتمل ہو گا۔ لیکن روتھ کی چھت بہرینڈ کے فرش سے بہت دور تھی۔ بہرینڈ نے دکھایا تھا کہ 0.06 سے 1 ملین کے درمیان عناصر میں سے 1 فیصد ترقی سے پاک سیٹ کے اندر فٹ ہو سکتے ہیں۔ اگرچہ روتھ کے فارمولے کا صحیح حساب لگانا مشکل ہے، لیکن یہ اس کم کے قریب کہیں بھی نہیں ہے - ایک موٹے اندازے کے مطابق اس کا فیصد تقریباً 40% ہے۔

لیکن اس خاص فرق سے زیادہ نمایاں دو فارمولوں کا مجموعی برتاؤ تھا۔ عناصر کا حصہ 1 اور کے درمیان پلاٹ کریں۔ N جس کی ہر فارمولہ نمائندگی کرتا ہے، اور آپ دیکھیں گے کہ Behrend کا نمبر تیزی سے سکڑ کر صفر تک پہنچتا ہے۔ N بڑھتا ہے دوسری طرف، روتھ کا حصہ صفر کی طرف پھسلتا ہے، لیکن آہستہ اور آہستہ۔ دونوں منحنی خطوط بہت مختلف شکلیں ہیں، اور ریاضی کی ترقی کے بغیر کسی سیٹ میں پڑے عناصر کا حقیقی تناسب، جہاں تک ریاضی دان جانتے تھے، ان کے درمیان کہیں بھی پڑ سکتے ہیں۔

گرین نے کہا کہ 1980 کی دہائی کے آغاز سے، "واقعی مشہور ریاضی دانوں کی ایک بڑی تعداد کی طرف سے، کافی حد تک بڑھنے والی بہتریوں کا ایک طویل سلسلہ تھا۔ ہر بار تھوڑی دیر میں، کوئی روتھ کی بالائی حد کو ایک یا دو بالوں سے نیچے دھکیل دیتا تھا، اور آخر کار یہ کافی کم ہو جاتا تھا۔ بہرینڈ کی نچلی حد، اس کے برعکس، کئی دہائیوں تک نہیں گھٹی۔ بلوم نے کہا کہ ریاضی دانوں نے سوچنا شروع کیا کہ شاید بہرینڈ صحیح جواب سے دور نہیں تھا۔

2023 کے اوائل میں کیلی اور میکا کے کاغذ کے آنے تک، بہرینڈ کے فارمولے کے ذریعے نیچے سے اور اوپر سے بلوم اور سیساسک کے ذریعے ترقی سے پاک سیٹ کا زیادہ سے زیادہ سائز لکھا گیا تھا۔ بلوم اور سیساسک کے جولائی 2020 کے پیپر نے یہ ظاہر کرتے ہوئے اہم "لوگارتھمک" حد کو عبور کر لیا تھا کہ ترقی سے پاک سیٹ کا کافی حد تک کم ہونا ضروری ہے۔ N/(لاگ N) عناصر. لیکن ان کا نتیجہ پھر بھی بہرینڈ کے اوپر بیٹھ گیا۔ کیلی اور میکا کا نیا اوپری باؤنڈ بہرینڈ کے سیٹ کردہ فرش کے بالکل قریب ہے۔

یو سی ایل اے کے ایک ممتاز ریاضی دان ٹیرینس تاؤ نے کہا، "میکا اور کیلی نے اس تمام اضافی پیش رفت کو چھلانگ لگا دی ہے۔"

ان کا فارمولہ تقریباً Behrend کے جیسا ہی ہے، جس میں صرف چند پیرامیٹرز کو ٹویک کیا گیا ہے۔ جیسا کہ N لامحدودیت کے قریب پہنچتے ہی، کیلی اور میکا کے فارمولے کا ایک پلاٹ آخر کار ایک منحنی خطوط میں آ جائے گا جو بہرینڈ وکر سے ملتا جلتا ہے۔ بلوم نے کہا، "اس شکل کا کوئی بھی پابند اس سے پہلے ایک ناممکن خواب کی طرح لگتا تھا۔

گرین نے کہا ، "میں واقعی میں کافی حیران تھا کہ انہوں نے اس طرح کی بہتری کی ہے۔"

ایک مختلف ٹیک

 اگرچہ کیلی اور میکا نے اس سے پہلے کبھی بھی خالص ریاضی کی تحقیق میں حصہ نہیں لیا تھا، لیکن ریاضی کی ترقی ان کے لیے اس وقت سے واقف تھی جب وہ شروع ہوئے۔ کیلی نے کہا کہ عام طور پر، کمپیوٹر سائنس دان "بھوک سے ایسی تکنیکوں کی تلاش کر رہے ہیں جو ہمارے مسائل کو حل کرنے کے لیے کام کریں گی۔" ترقی سے پاک سیٹ کے سائز کا مطالعہ کرنے کے لیے تاریخی طور پر استعمال ہونے والے ٹولز کمپیوٹر سائنس کے سب فیلڈ آف کمپلیکٹی تھیوری میں بڑے پیمانے پر استعمال ہو چکے ہیں۔ اس طرح کے سیٹ کے سائز کو کم کرنے کا مسئلہ پیچیدگی کے تھیورسٹوں کے لیے ایسی تکنیکوں کے استعمال کی ایک عمدہ مثال کے طور پر جانا جاتا ہے جو سیٹوں کی اندرونی ساخت کی تحقیقات کرتی ہیں۔

2021 کے آخر میں، کیلی اور میکا ان امکانات کا تجزیہ کر رہے تھے کہ کسی خاص کوآپریٹو گیم میں کھلاڑیوں کی ایک ٹیم جیت سکے گی، جو کہ کمپیوٹر سائنس کا ایک معیاری مسئلہ ہے۔ یہ ان کے سامنے آیا کہ ترقی سے پاک سیٹوں کے سائز پر تحقیق کی تکنیک مددگار ثابت ہو سکتی ہے۔ لیکن انہوں نے ان تکنیکوں کو کوآپریٹو گیم میں لاگو کرنے کے بجائے براہ راست مطالعہ کرنا آسان پایا۔ کیلی نے کہا، "اس مسئلے پر کس طرح پیش رفت کرنا ہے اس کے لیے میرا بہترین خیال [یہ تھا] کہ اصل میں اس آلے کو بہتر بنایا جائے، نہ کہ اسے زیادہ ہوشیار طریقے سے استعمال کرنا،" کیلی نے کہا۔

"کسی وقت، ہم نے صرف اس سوال پر براہ راست کام کرنے کا فیصلہ کیا،" میکا نے یاد کیا۔ چھ ماہ بعد، دونوں محققین نے اپنی حکمت عملی کا اندازہ لگا لیا تھا اور انہیں صرف اس بات کی ضرورت تھی کہ اس مسئلے پر اپنا طریقہ کار کیسے لاگو کیا جائے۔

یہ دیکھنے کے لیے کہ وہ اپنی نئی بالائی حد تک کیسے پہنچے، 1 اور کے درمیان نمبروں کا کوئی بھی سیٹ لیں۔ N. اسے بلاؤ A. کی کثافت A 1 اور کے درمیان نمبروں کا فیصد ہے۔ N کہ اس میں شامل ہے. چونکہ 1 اور کے درمیان ریاضی کی بہت سی ممکنہ پیشرفتیں ہیں۔ N، اگر آپ کے عناصر کا انتخاب نہیں کرتے ہیں۔ A احتیاط سے، کوئی بھی A اعلی کثافت کے ساتھ ممکنہ طور پر ریاضی کی بہت ساری پیشرفتیں شامل ہوں گی۔

ان کے ثبوت میں، کیلی اور میکا نے اس کا تصور کیا۔ A کچھ یا کوئی ریاضی کی ترقی نہیں تھی، اور انہوں نے نتائج کا پتہ لگانے کی کوشش کی۔ اگر A کافی گھنے تھے، انہوں نے ظاہر کیا کہ ترقی کی غیر موجودگی کے اندر اندر ساخت کی سطح کی ضرورت ہوتی ہے۔ A اس کا نتیجہ لازمی طور پر ایک تضاد کا باعث بنے گا، یعنی کہ A سب کے بعد، کم از کم ایک ترقی پر مشتمل ہونا ضروری ہے.

اس ساخت کو سمجھنے کے لیے انہوں نے سیٹ پر غور کیا۔ A + A، جو کے دو عناصر کو شامل کرکے بنائے گئے تمام اعداد پر مشتمل ہے۔ A. انہوں نے محسوس کیا کہ اگر A نسبتاً چند ریاضی کی پیشرفت پر مشتمل ہے، اس کا مطلب ہے کے عناصر کے درمیان بے کار پن A + A: سے اعداد کے مختلف جوڑے A اکثر ایک ہی نمبر میں اضافہ کریں۔

کثافت کی تعریف نہ صرف 1 اور کے درمیان تمام عدد کے مقابلے میں کی جا سکتی ہے۔ N لیکن کچھ ذیلی سیٹ کے مقابلے میں - اس وقفہ میں صرف یکساں عدد، یا صرف 3 کے ضرب۔ A + A انٹیجرز کا سب سیٹ تلاش کرنے کے لیے جہاں کے عناصر A خاص طور پر عام تھے۔

اگر A میں غیر متناسب طور پر 3 کے کئی ضرب ہوتے ہیں، مثال کے طور پر، کیلی اور میکا پھر اس حصے پر توجہ مرکوز کریں گے جس میں 3 کے ضرب شامل تھے۔ انہوں نے اس حکمت عملی کو بار بار دہرایا۔ ہر بار انہیں عدد کے چھوٹے اور چھوٹے ذیلی سیٹ ملے، جن پر Aکی کثافت بڑھتی اور بڑھتی رہے گی۔ مثال کے طور پر، A 10 اور کے درمیان 1% عدد پر مشتمل ہو سکتا ہے۔ Nاس وقفہ میں 15 کے ضرب کا 3%، اور 25 کے یکساں ضرب کا 3%۔

جب کچھ دلچسپ ہوتا ہے۔ A بڑا ہے. اگر طریقہ کار کو دہرایا جاتا ہے تو، کی کثافت A کچھ سب سیٹ سے زیادہ 100% سے زیادہ ہے۔ یہ، یقینا، ناممکن ہے. A 24 کے تمام ضربوں پر مشتمل ہو سکتا ہے، لیکن یہ ان سب سے زیادہ پر مشتمل نہیں ہو سکتا۔ یہ تضاد صرف اس صورت میں پیدا ہوتا ہے۔ A شروع کرنے کے لئے کافی بڑا ہے، لیکن جب ایسا ہوتا ہے، تو اس کا مطلب یہ ہے کہ مفروضہ A اس میں کوئی ریاضی کی پیشرفت نہیں ہونی چاہیے غلط ہو گی۔

یہ ایک "جیت کی دلیل" ہے، جب A بڑا ہے، میکا نے کہا۔ یا تو A ریاضی کی بہت ساری پیشرفتیں شامل ہیں، یا اس میں بہت زیادہ فالتو پن ہے۔ A + A - جس صورت میں وہ سب سیٹ تلاش کرنے کا طریقہ کار استعمال کر سکتے ہیں (جسے "کثافت میں اضافے کی حکمت عملی" کہا جاتا ہے) یہ ظاہر کرنے کے لیے کہ ایک پیشرفت ظاہر ہونی چاہیے۔ A. اگرچہ کثافت میں اضافے کی حکمت عملی میدان میں ایک اچھی طرح سے پہنا ہوا خاکہ ہے، لیکن کیلی اور میکا اسے چھوٹے کام کرنے میں کامیاب ہو گئے۔ Aپہلے سے کہیں زیادہ ہے۔ اس کے ساتھ، انہوں نے ترقی سے پاک سیٹ کے سائز کے لیے ایک نئی چھت کا انکشاف کیا۔

کیلی اور میکا نے کثافت میں اضافے کے بلیو پرنٹ سے خیالات کا ایک انوکھا امتزاج بنایا۔ بالکل نئے فریم ورک کے ساتھ آنے کے بجائے، انہوں نے اپنے گھنے ذیلی سیٹ کو تلاش کرنے کے طریقے پر دوبارہ غور کیا۔ اس کے لیے، انہوں نے ایک تکنیک کا استعمال کیا جسے وہ "sifting" کہتے ہیں، جس میں اپنے سیٹ کو ایک مستقل رقم سے منتقل کرنا، اسے اپنے ساتھ جوڑنا، اور اس عمل کو کئی بار دہرانا شامل ہے۔ چوراہے کے کئی چکروں کے بعد جو باقی رہ جاتا ہے، وہ پیشین گوئی کے قابل خصوصیات کے ساتھ ایک انتہائی ساختہ سیٹ ہے۔ اگرچہ sifting دوسرے کاغذات میں استعمال کیا گیا ہے، یہ تین مدتی ترقی کے مسئلے پر کبھی نہیں آزمایا گیا تھا.

پیچھے کی طرف دیکھ رہا ہوں

کیلی اور میکا نے روایتی طریقوں میں چھاننے جیسے نظرانداز شدہ ٹولز کو انجیکشن لگا کر چونکا دینے والی رقم سے ترقی سے پاک سیٹ کی سائز کی حد کو نیچے کھینچ لیا۔ بلوم نے کہا، "کیلی اور میکا نے ہمیں دکھایا ہے کہ کسی نہ کسی طرح یہ تکنیکیں، جو وہاں کھلے میں بیٹھی ہوئی تھیں، اس سے کہیں زیادہ طاقتور تھیں جتنا ہم نے سوچا تھا،" بلوم نے کہا۔ ان ٹولز کی نئی افادیت کی روشنی میں، انہوں نے مزید کہا، "ہمیں واپس جانا ہوگا اور ہر چیز پر نظر ثانی کرنی ہوگی۔"

کثافت میں اضافے کی حکمت عملی پہلی بار 70 سال پہلے روتھ کے مقالے میں شائع ہوئی تھی اور اس کے بعد سے ریاضی کی ترقی پر زیادہ تر کاغذات میں استعمال ہوتی رہی ہے۔ گرین حیران تھا کہ فریم ورک کو کیلی اور میکا کی حد تک کم ثابت کرنے کے لیے استعمال کیا جا سکتا ہے۔ "میں نے سوچا کہ کچھ مکمل طور پر، یکسر مختلف کی ضرورت ہوگی،" انہوں نے کہا۔

کیلی ریاضی میں اپنا سفر جاری رکھنے کے لیے پرجوش ہے۔ انہوں نے کہا کہ "میرے پاس بہت سے مختلف مسائل پر امیدوں اور خوابوں کی کوئی کمی نہیں ہے جن پر میں کم از کم روحانی طور پر اس سے متعلق سوچوں گا۔"

کہ کیلی اور میکا نے ایک بار نظر انداز کیے جانے والے خیالات کی طاقت کا پتہ لگانے میں کامیابی حاصل کی جو ریاضی کی ترقی کی اکثر موزوں نوعیت کو ظاہر کرتی ہے - ایک ایسی خوبی جو تاؤ کے لیے لعنت سے زیادہ ایک نعمت ہے۔ "یہ ہمیشہ ایسا نہیں ہوتا ہے کہ ریاضی مشکل سے مشکل تر ہوتا چلا جاتا ہے،" انہوں نے کہا۔ "خدا کا شکر ہے."