1850 میں تھامس پینینگٹن کرک مین، ایک ریاضی دان جب چرچ آف انگلینڈ میں ایک وائکر کے طور پر اپنی اہم ذمہ داری پوری نہیں کر رہا تھا، اس نے اپنے "اسکول گرل کے مسئلے" کو بیان کیا: "ایک اسکول میں پندرہ نوجوان خواتین لگاتار سات دن تک تین بار باہر چلتی ہیں: اس کا انتظام کرنا ضروری ہے۔ انہیں روزانہ، تاکہ کوئی بھی دو بار برابر نہ چل سکے۔
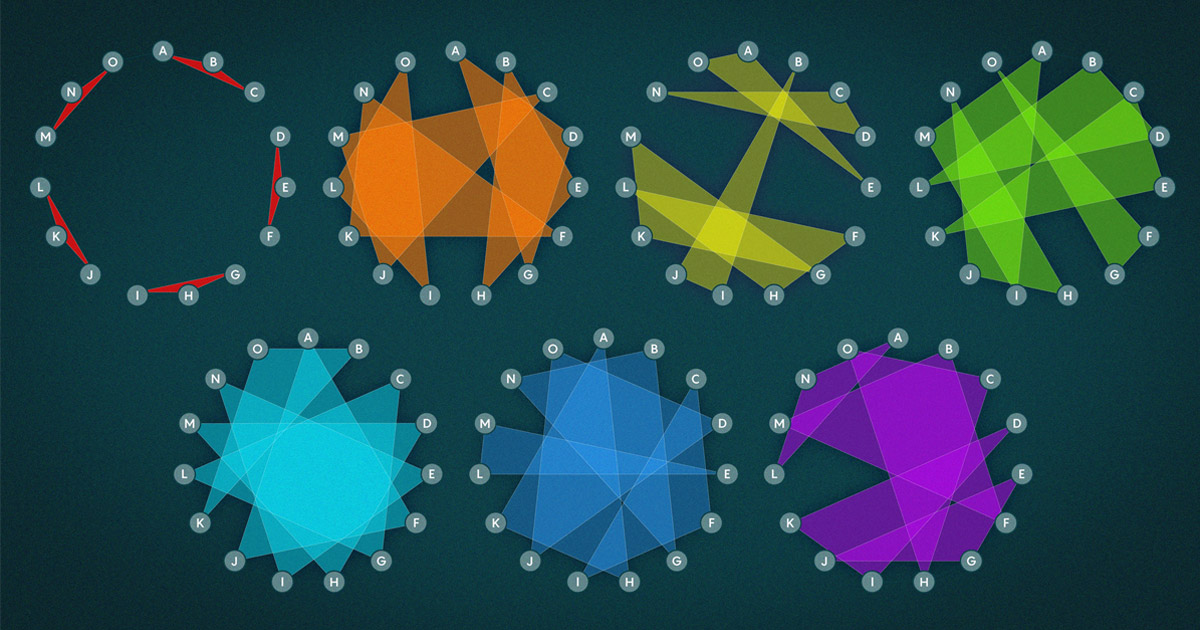
ایک جدید ریاضی دان کے لیے، اس قسم کے مسئلے کا بہترین تصور ہائپر گراف کے طور پر کیا جاتا ہے - تین یا اس سے زیادہ کے گروپوں میں جمع کردہ نوڈس کا ایک سیٹ۔ اسکول کی 15 لڑکیاں نوڈس ہیں، اور "تین برابر" کے ہر گروپ کو ایک مثلث کے طور پر سوچا جا سکتا ہے، جس میں تین لائنیں، یا کنارہ، تین نوڈس کو جوڑتا ہے۔
کرک مین کا مسئلہ بنیادی طور پر یہ پوچھتا ہے کہ کیا ان مثلثوں کا کوئی انتظام ہے جو تمام سکول کی طالبات کو ایک دوسرے سے جوڑتا ہے، لیکن اس اضافی پابندی کے ساتھ کہ کوئی دو مثلث ایک کنارے کا اشتراک نہیں کرتا ہے۔ ایج شیئرنگ کا مطلب یہ ہوگا کہ اسکول کی دو لڑکیوں کو ایک سے زیادہ بار ساتھ چلنا پڑتا ہے۔ اس پابندی کا مطلب ہے کہ ہر لڑکی ایک ہفتے کے لیے ہر روز دو نئے دوستوں کے ساتھ چلتی ہے، تاکہ ہر ممکنہ جوڑا بالکل ایک بار اکٹھا ہو۔
یہ مسئلہ اور اس جیسے دیگر نے تقریباً دو صدیوں سے ریاضی دانوں کو گمراہ کیا ہے جب سے کرک مین نے اپنا سوال اٹھایا ہے۔ 1973 میں، افسانوی ریاضی دان پال ایرڈس نے اسی طرح کی تصویر پیش کی۔ اس نے پوچھا کہ کیا دو بظاہر غیر مطابقت پذیر خصوصیات کے ساتھ ہائپر گراف بنانا ممکن ہے۔ سب سے پہلے، نوڈس کے ہر جوڑے کو بالکل ایک مثلث سے جوڑا جانا چاہیے، جیسا کہ اسکول کی لڑکیوں کے ساتھ ہے۔ یہ خاصیت گراف کو مثلث کے ساتھ گھنے بناتی ہے۔ دوسری ضرورت اس بات پر مجبور کرتی ہے کہ مثلث کو بالکل درست طریقے سے پھیلایا جائے۔ (خاص طور پر، اس کا تقاضا ہے کہ مثلث کے کسی بھی چھوٹے گروپ کے لیے، مثلث کے مقابلے میں کم از کم تین مزید نوڈس ہوں۔) "آپ کا یہ قدرے متضاد رویہ ہے جہاں آپ کے پاس ایک گھنی مجموعی چیز ہے جس کے کوئی گھنے حصے نہیں ہیں،" کہا۔ ڈیوڈ کونلنکیلیفورنیا انسٹی ٹیوٹ آف ٹیکنالوجی میں ریاضی دان۔
اس جنوری میں، 50 صفحات کا ایک پیچیدہ ثبوت، چار ریاضی دانوں نے ثابت کیا کہ جب تک آپ کے پاس کافی نوڈس ہوں اس طرح کا ہائپر گراف بنانا ہمیشہ ممکن ہے۔ "صرف اسے حاصل کرنے کے لیے جس تکنیکی صلاحیت سے گزرا، یہ حیرت انگیز تھا،" کہا ایلن لو، برمنگھم یونیورسٹی میں ایک ریاضی دان۔ کونلن نے اتفاق کیا: "یہ واقعی ایک متاثر کن کام ہے۔"
تحقیقی ٹیم نے ایک ایسا نظام بنایا جس نے مثلث کے انتخاب کے لیے ایک بے ترتیب عمل کے ساتھ شروع کرکے اور ان کی ضروریات کو پورا کرنے کے لیے انتہائی احتیاط کے ساتھ اس کی انجینئرنگ کرکے اردس کی شیطانی ضروریات کو پورا کیا۔ کونلون نے کہا، "ثبوت میں جانے والی مشکل ترامیم کی تعداد دراصل حیران کن ہے۔"
ان کی حکمت عملی انفرادی مثلث سے ہائپر گراف کو احتیاط سے تیار کرنا تھی۔ مثال کے طور پر، ہماری 15 سکول کی لڑکیوں کا تصور کریں۔ ہر جوڑے کے درمیان ایک لکیر کھینچیں۔
یہاں مقصد یہ ہے کہ ان لائنوں کے اوپر مثلث کا پتہ لگانا اس طرح ہے کہ مثلث دو تقاضوں کو پورا کریں: پہلا، کوئی دو مثلث ایک کنارے کا اشتراک نہیں کرتے ہیں۔ (اس ضرورت کو پورا کرنے والے سسٹمز کو سٹینر ٹرپل سسٹم کہا جاتا ہے۔) اور دوسرا، اس بات کو یقینی بنائیں کہ مثلث کا ہر چھوٹا ذیلی سیٹ کافی بڑی تعداد میں نوڈس کا استعمال کرے۔
جس طرح سے محققین نے ایسا کیا اسے شاید مشابہت کے ساتھ سب سے بہتر سمجھا جاتا ہے۔
کہیں کہ کناروں سے مثلث بنانے کے بجائے، آپ لیگو اینٹوں سے گھر بنا رہے ہیں۔ پہلی چند عمارتیں جو آپ بناتے ہیں اسراف ہیں، ساختی کمک اور وسیع آرائش کے ساتھ۔ ایک بار جب آپ ان کے ساتھ کام کر لیں تو انہیں ایک طرف رکھ دیں۔ وہ ایک "جذب کرنے والے" کے طور پر کام کریں گے - ایک قسم کا منظم ذخیرہ۔
اب اپنی باقی ماندہ اینٹوں سے عمارتیں بنانا شروع کریں، بغیر کسی منصوبہ بندی کے آگے بڑھیں۔ جب آپ کی Legos کی سپلائی کم ہو جاتی ہے، تو ہو سکتا ہے کہ آپ اپنے آپ کو کچھ آوارہ اینٹوں، یا ایسے گھر پائیں جو ساختی طور پر ناقص ہوں۔ لیکن چونکہ جذب کرنے والی عمارتیں بہت زیادہ کام کرتی ہیں اور مضبوط ہوتی ہیں، اس لیے آپ یہاں اور وہاں سے کچھ اینٹیں نکال سکتے ہیں اور تباہی کا سامنا کیے بغیر انہیں استعمال کر سکتے ہیں۔
سٹینر ٹرپل سسٹم کے معاملے میں، آپ مثلث بنانے کی کوشش کر رہے ہیں۔ آپ کا جاذب، اس معاملے میں، کناروں کا احتیاط سے منتخب کردہ مجموعہ ہے۔ اگر آپ اپنے آپ کو باقی نظام کو مثلث میں ترتیب دینے سے قاصر محسوس کرتے ہیں، تو آپ کچھ کناروں کو استعمال کر سکتے ہیں جو جاذب میں لے جاتے ہیں۔ پھر، جب آپ یہ کر لیتے ہیں، تو آپ جاذب کو ہی مثلث میں توڑ دیتے ہیں۔
جذب ہمیشہ کام نہیں کرتا۔ لیکن ریاضی دانوں نے اس عمل کے ساتھ گھل مل گئے ہیں، رکاوٹوں کو دور کرنے کے لیے نئے طریقے تلاش کیے ہیں۔ مثال کے طور پر، ایک طاقتور ویرینٹ جسے تکراری جذب کہا جاتا ہے، کناروں کو سیٹوں کے نیسٹڈ ترتیب میں تقسیم کرتا ہے، تاکہ ہر ایک اگلے بڑے کے لیے ایک جاذب کے طور پر کام کرے۔
"پچھلی دہائی یا اس سے زیادہ عرصے میں بڑے پیمانے پر بہتری آئی ہے،" کونلن نے کہا۔ "یہ ایک آرٹ کی شکل ہے، لیکن انہوں نے واقعی اس مقام پر اسے اعلیٰ فن کی سطح تک پہنچایا ہے۔"
Erdős کا مسئلہ تکراری جذب کے ساتھ بھی مشکل تھا۔ "یہ بہت جلد واضح ہو گیا کہ یہ مسئلہ کیوں حل نہیں ہوا،" کہا مہتاب ساہنی، ان چار محققین میں سے ایک جنہوں نے اسے حل کیا، اس کے ساتھ اشون ساہ، جو ساہنی کے ساتھ میساچوسٹس انسٹی ٹیوٹ آف ٹیکنالوجی میں گریجویٹ طالب علم ہے۔ مائیکل سمکن, ہارورڈ یونیورسٹی میں سینٹر آف میتھمیٹکل سائنسز اینڈ ایپلیکیشنز میں پوسٹ ڈاکٹریٹ فیلو؛ اور میتھیو کوانانسٹی ٹیوٹ آف سائنس اینڈ ٹیکنالوجی آسٹریا میں ایک ریاضی دان۔ "وہاں کافی دلچسپ، کافی مشکل تکنیکی کام تھے۔"
مثال کے طور پر، تکراری جذب کی دوسری ایپلی کیشنز میں، ایک بار جب آپ کسی سیٹ کا احاطہ مکمل کر لیتے ہیں — یا تو مثلث کے ساتھ، سٹینر کے ٹرپل سسٹمز کے لیے، یا دیگر مسائل کے لیے دوسرے ڈھانچے کے ساتھ — آپ اس پر غور کر سکتے ہیں اور اسے بھول سکتے ہیں۔ تاہم، اردس کے حالات نے چاروں ریاضی دانوں کو ایسا کرنے سے روک دیا۔ مثلث کا ایک مشکل جھرمٹ آسانی سے متعدد جاذب سیٹوں سے نوڈس کو شامل کرسکتا ہے۔
ساہنی نے کہا، "ایک مثلث جسے آپ نے 500 قدم پہلے چنا تھا، آپ کو کسی نہ کسی طرح یاد رکھنا ہوگا کہ اس کے بارے میں کیسے سوچنا ہے۔"
ان چاروں نے آخر کار جو کچھ سوچا وہ یہ تھا کہ اگر وہ اپنے مثلث کا انتخاب احتیاط سے کریں تو وہ ہر چھوٹی چیز پر نظر رکھنے کی ضرورت کو ختم کر سکتے ہیں۔ ساہنی نے کہا کہ "اس سے بہتر ہے کہ 100 تکونوں کے کسی بھی چھوٹے سیٹ کے بارے میں سوچا جائے اور اس بات کی ضمانت دی جائے کہ مثلث کے سیٹ کا انتخاب درست امکان کے ساتھ کیا گیا ہے۔"
نئے مقالے کے مصنفین پر امید ہیں کہ ان کی تکنیک کو اس ایک مسئلے سے آگے بڑھایا جا سکتا ہے۔ ان کے پاس پہلے ہی اپنی حکمت عملی کا اطلاق کر چکے ہیں۔ کے بارے میں ایک مسئلہ لاطینی چوکور، جو سوڈوکو پہیلی کو آسان بنانے کی طرح ہیں۔
کوان نے کہا کہ اس کے علاوہ، بہت سے سوالات ہیں جو بالآخر جذب کرنے کے طریقوں کو حاصل کر سکتے ہیں۔ "کمبینیٹرکس میں بہت سارے مسائل ہیں، خاص طور پر ڈیزائن تھیوری میں، جہاں بے ترتیب عمل واقعی ایک طاقتور ٹول ہیں۔" ایسا ہی ایک مسئلہ، Ryser-Brualdi-Stein قیاس، لاطینی مربعوں کے بارے میں بھی ہے اور 1960 کی دہائی سے اس کے حل کا انتظار ہے۔
اگرچہ اس مسئلے کو ختم کرنے سے پہلے جذب کو مزید ترقی کی ضرورت ہو سکتی ہے، لیکن اس نے 30 سال پہلے اپنے آغاز کے بعد سے ایک طویل سفر طے کیا ہے، کہا۔ مایا سٹین، چلی یونیورسٹی میں ریاضی کے ماڈلنگ کے مرکز کے ڈپٹی ڈائریکٹر۔ "یہ وہ چیز ہے جو دیکھنے میں واقعی بہت اچھا ہے کہ یہ طریقے کیسے تیار ہوتے ہیں۔"