حیران کن طور پر سادہ ریاضی حیران کن میچ اپ کے پیچھے | کوانٹا میگزین

یہ امیجنری میتھ لیگ کا چیمپئن شپ گیم ہے، جہاں اٹلانٹا الجبراز کا مقابلہ کیرولینا کراس پروڈکٹس سے ہوگا۔ دونوں ٹیمیں اس سیزن میں ایک دوسرے سے نہیں کھیلی ہیں، لیکن سال کے شروع میں اٹلانٹا نے بروکلین بائیسیکٹرز کو 10 سے 5 کے اسکور سے شکست دی تھی، اور بروکلین نے کیرولینا کو 7 سے 3 کے اسکور سے شکست دی تھی۔ کیا اس سے ہمیں کوئی بصیرت ملتی ہے کہ کون عنوان لے گا؟

ٹھیک ہے، یہاں سوچ کی ایک لائن ہے. اگر اٹلانٹا نے بروکلین کو شکست دی، تو اٹلانٹا بروکلین سے بہتر ہے، اور اگر بروکلین نے کیرولینا کو شکست دی، تو بروکلین کیرولینا سے بہتر ہے۔ لہذا، اگر اٹلانٹا بروکلین سے بہتر ہے اور بروکلین کیرولینا سے بہتر ہے، تو اٹلانٹا کو کیرولینا سے بہتر ہونا چاہیے اور چیمپئن شپ جیتنی چاہیے۔

اگر آپ مسابقتی کھیل یا کھیل کھیلتے ہیں، تو آپ جانتے ہیں کہ میچ کے نتائج کی پیش گوئی کرنا کبھی بھی اتنا سیدھا نہیں ہوتا۔ لیکن مکمل طور پر ریاضیاتی نقطہ نظر سے، اس دلیل میں کچھ اپیل ہے. یہ ریاضی میں ایک اہم خیال کا استعمال کرتا ہے جسے ٹرانزیٹویٹی کے نام سے جانا جاتا ہے، ایک جانی پہچانی خاصیت جو ہمیں تمام رشتوں میں موازنہ کی تاریں بنانے کی اجازت دیتی ہے۔ Transitivity ان ریاضیاتی خصوصیات میں سے ایک ہے جو اتنی بنیادی ہے کہ شاید آپ اسے محسوس بھی نہ کریں۔

مثال کے طور پر، اعداد کی مساوات عبوری ہے۔ اس کا مطلب یہ ہے کہ اگر ہم جانتے ہیں۔ a = b اور b = c، ہم یہ نتیجہ اخذ کر سکتے ہیں۔ a = c. "سے بڑا" تعلق بھی عبوری ہے: حقیقی اعداد کے لیے، اگر a > b اور b > c، تو a > c. جب تعلقات عبوری ہوتے ہیں، تو ہم ان کا موازنہ اور یکجا کر سکتے ہیں، جس سے اشیاء کی ترتیب پیدا ہوتی ہے۔ اگر انا بینجی سے لمبا ہے اور بینجی کارل سے لمبا ہے، تو ہم ان تینوں کو ان کی اونچائی کے حساب سے ترتیب دے سکتے ہیں: A, B, C. ہماری اس بے ہودہ دلیل کے پیچھے بھی Transitivity کارفرما ہے کہ اگر A سے بہتر ہے B اور B سے بہتر ہے C، تو A سے بہتر ہے C.

مساوات، ہم آہنگی، مماثلت، یہاں تک کہ متوازی میں بھی عبوریت موجود ہے۔ یہ ان تمام بنیادی ریاضی کا حصہ ہے جو ہم کرتے ہیں، جو اسے خاص طور پر ریاضی کے لحاظ سے دلچسپ بناتا ہے جب یہ وہاں نہ ہو۔ جب تجزیہ کار ٹیموں کی درجہ بندی کرتے ہیں، ماہرین اقتصادیات صارفین کی ترجیحات کا مطالعہ کرتے ہیں، یا شہری اپنے پسندیدہ امیدواروں کو ووٹ دیتے ہیں، تو منتقلی کی کمی حیران کن نتائج کا باعث بن سکتی ہے۔ اس قسم کے نظاموں کو بہتر طور پر سمجھنے کے لیے، ریاضی دان 50 سال سے زیادہ عرصے سے "intransitive dice" کا مطالعہ کر رہے ہیں، اور ایک حالیہ کاغذ پولی میتھ پروجیکٹ کے نام سے جانا جاتا آن لائن ریاضی کے تعاون سے اس سمجھ کو آگے بڑھایا گیا ہے۔ اس بات کا احساس حاصل کرنے کے لیے کہ ہم آہنگی کیسی دکھتی ہے اور کیسی محسوس ہوتی ہے، آئیے اپنی ایک لیگ بنائیں اور اس کے ارد گرد کھیلیں۔

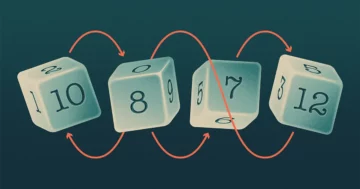
ہماری نئی میتھ لیگ میں، کھلاڑی حسب ضرورت سکے پلٹ کر اور نتائج کا موازنہ کر کے مقابلہ کرتے ہیں۔ آئیے کھلاڑی کہتے ہیں۔ A ایک سکہ ہے جس کے ایک طرف نمبر 10 اور دوسری طرف نمبر 6 ہے، اور پلیئر Bکے سکے کے نمبر 8 اور 3 ہیں۔ ہم فرض کریں گے کہ سکے منصفانہ ہیں — یعنی جب سکے پلٹ جائیں گے تو ہر طرف کا یکساں طور پر ظاہر ہونے کا امکان ہے — اور ہم سکوں پر نمبروں کی اس طرح نمائندگی کریں گے۔

ایک کھیل میں، کھلاڑی اپنے سکے پلٹتے ہیں، اور جس کا سکہ زیادہ نمبر دکھاتا ہے وہ فاتح ہوتا ہے۔ کون جیتے گا کب A ادا کرتا ہے B?

یقینا، یہ منحصر ہے. کبھی کبھی A کبھی کبھی جیت جائے گا B جیت جائے گا. لیکن یہ دیکھنا مشکل نہیں ہے۔ A کے خلاف جیتنے کے حق میں ہے۔ B. کھیل کے سامنے آنے کے چار طریقے ہیں، اور A ان میں سے تین میں جیتتا ہے۔

تو کے کھیل میں A بنام B, A جیتنے کا 75 فیصد امکان ہے۔

ابھی C ساتھ آتا ہے اور چیلنج کرتا ہے۔ B ایک کھیل کے لئے. Cکے سکے کے ایک طرف 5 اور دوسری طرف 4 ہے۔ ایک بار پھر چار امکانات ہیں۔

یہاں B اور C ہر ایک چار میں سے دو میچ اپ جیتتا ہے، لہذا وہ ہر ایک 50% گیمز جیتیں گے۔ B اور C یکساں طور پر مماثل ہیں۔

اب، آپ کب کیا ہونے کی توقع کریں گے۔ A اور C کھیلیں؟ ٹھیک ہے، A عام طور پر دھڑکتا ہے B، اور B کے ساتھ یکساں طور پر مماثل ہے۔ C، لہذا اس کی توقع کرنا مناسب معلوم ہوتا ہے۔ A شاید کے خلاف حمایت کی جائے گی C.

لیکن A ایک پسندیدہ سے زیادہ ہے. A غلبہ C، 100% وقت جیتنا۔

یہ حیران کن معلوم ہو سکتا ہے، لیکن ریاضیاتی طور پر یہ دیکھنا مشکل نہیں ہے کہ ایسا کیوں ہوتا ہے۔ Cکے نمبر درمیان میں ہیں۔ Bکی، تو C کسی بھی وقت جیت جاتا ہے B ان کے نچلے نمبر کو پلٹتا ہے۔ لیکن Cکے نمبر دونوں نیچے ہیں۔ Aکی، تو C وہ میچ کبھی نہیں جیتیں گے۔ یہ مثال منتقلی کے خیال کی خلاف ورزی نہیں کرتی ہے، لیکن اس سے یہ ظاہر ہوتا ہے کہ چیزیں محض اس سے زیادہ پیچیدہ ہو سکتی ہیں A > B > C. ہمارے گیم میں تھوڑی سی تبدیلی ظاہر کرتی ہے کہ یہ کتنا زیادہ پیچیدہ ہو سکتا ہے۔

ہمارے حریف دو رخی سکوں کے پلٹنے والے کھیل سے تیزی سے تھک جاتے ہیں، کیونکہ اسے مکمل طور پر ریاضی سے سمجھنا آسان ہے (مزید تفصیلات کے لیے کالم کے آخر میں مشقیں دیکھیں)، اس لیے لیگ تین رخی سکوں میں اپ گریڈ کرنے کا فیصلہ کرتی ہے۔ (ایک خیالی ریاضی کی لیگ میں کھیلنے کا ایک فائدہ یہ ہے کہ کچھ بھی ممکن ہے۔)

یہاں ہیں A اور Bکے سکے:

جس کے درمیان کھیل میں پسند کیا جاتا ہے۔ A اور B? ٹھیک ہے، کے لئے تین نتائج ہیں Aکے سکے ٹاس اور تین کے لیے B، جس سے نو ممکنہ کھیل کے نتائج نکلتے ہیں جنہیں ہم آسانی سے چارٹ کر سکتے ہیں۔

ایک بار پھر یہ فرض کرتے ہوئے کہ تمام نتائج کا امکان یکساں ہے، A دھڑک رہا ہے B نو نتائج میں سے پانچ میں۔ اسکا مطلب A $latex frac{5}{9} وقت کا تقریبا$ 55% جیتنا چاہئے، لہذا A کے خلاف پسند کیا جاتا ہے۔ B.

ان کے امکانات کے بارے میں تھوڑا سا نیچے محسوس کرنا، B چیلنجوں C ایک کھیل کے لئے. Cکے نمبر ذیل میں دکھائے گئے ہیں۔ کیا تمہیں پسند ہے Bکے امکانات؟

ایک بار پھر، کے ایک کھیل میں نو ممکنہ نتائج ہیں۔ B بنام C، تو ہم صرف ان کی فہرست بنا سکتے ہیں۔

ہم اسے دیکھ سکتے ہیں B کے خلاف بہت اچھا لگ رہا ہے C. نو ممکنہ نتائج میں سے پانچ میں، B جیتتا ہے تو B کے خلاف پسند کیا جاتا ہے۔ C.

غریب C اب کھیلنا ہے A. کے ساتھ A کے خلاف حمایت کی B اور B کے خلاف حمایت کی C، کیا موقع کرتا ہے C جیتنا ہے؟ ایک بہت اچھا، جیسا کہ یہ پتہ چلتا ہے۔

یہاں نو میں سے پانچ ممکنہ نتائج میں، C دھڑک رہا ہے A. اس کا مطلب ہے کہ C کے خلاف پسند کیا جاتا ہے۔ A، اگرچہ Aکے خلاف پسند کیا جاتا ہے۔ B اور B کے خلاف پسند کیا جاتا ہے۔ C.

یہ ایک غیر معمولی نظام کی ایک مثال ہے۔ مزید تکنیکی اصطلاحات میں، ہمارے کھیل میں تعلق "کے خلاف پسند کیا جا رہا ہے" عارضی نہیں ہے: A کے خلاف پسند کیا جاتا ہے۔ B، اور B کے خلاف پسند کیا جاتا ہے۔ C، لیکن A ضروری نہیں کہ اس کے خلاف پسند کیا جائے۔ C.

ہم اسے اکثر ریاضی میں نہیں دیکھتے ہیں، لیکن اس قسم کا رویہ کھیلوں کے شائقین کو حیران نہیں کرے گا۔ اگر جنات نے عقابوں کو شکست دی اور عقاب نے کاؤبای کو شکست دی تو کاؤبای اب بھی جنات کو بہت اچھی طرح سے شکست دے سکتے ہیں۔ بہت سارے عوامل ہیں جو انفرادی کھیل کے نتائج میں حصہ ڈالتے ہیں۔ ٹیمیں مشق کے ساتھ بہتر ہوسکتی ہیں یا اگر وہ اختراع نہیں کرتی ہیں تو جمود کا شکار ہوسکتی ہیں۔ کھلاڑی ٹیمیں بدل سکتے ہیں۔ گیم کے مقام جیسی تفصیلات — گھر پر یا باہر — یا حال ہی میں ٹیموں نے کس طرح کھیلا ہے اس پر اثر پڑ سکتا ہے کہ کون جیتا اور کون ہارتا ہے۔

لیکن یہ سادہ سی مثال یہ ظاہر کرتی ہے کہ اس قسم کی مداخلت کے پیچھے بھی خالصتاً ریاضیاتی وجوہات ہیں۔ اور یہ خالصتاً ریاضیاتی غور مسابقت کی حقیقی دنیا کی رکاوٹوں کے ساتھ کچھ مشترک ہے: میچ اپس۔

کے لیے نمبر یہ ہیں۔ A, B اور C.

جب ہم انہیں ساتھ ساتھ دیکھتے ہیں، تو یہ دیکھنا آسان ہو جاتا ہے کہ اس صورت حال میں عدم منتقلی کیوں ہوتی ہے۔ اگرچہ B کے خلاف جیتنے کے حق میں ہے۔ C, Cکے دو درمیانے درجے کے نمبر - 7 اور 6 - انہیں ایک فائدہ دیتے ہیں۔ A کہ B نہیں ہے اگرچہ A کے خلاف پسند کیا جاتا ہے۔ B اور B کے خلاف پسند کیا جاتا ہے۔ C, C کے خلاف میچ کرتا ہے۔ A سے بہتر B کرتا ہے یہ اس سے ملتا جلتا ہے کہ کس طرح ایک انڈر ڈاگ اسپورٹس ٹیم کسی اعلی حریف کے خلاف اچھی طرح سے میچ کر سکتی ہے کیونکہ ان کے کھیل کا انداز اس ٹیم کے لیے ہینڈل کرنا مشکل ہے، یا اس وجہ سے کہ کوئی کھلاڑی یا کوچ انہیں اس مخصوص حریف کے خلاف برتری دیتا ہے۔

حقیقت یہ ہے کہ کھیل غیر متضاد ہیں اس کا حصہ ہے جو انہیں تفریح ​​​​اور مجبور بناتا ہے۔ سب کے بعد، اگر A دھڑک رہا ہے B اور B دھڑک رہا ہے C, C جب ان کا سامنا کرنا پڑتا ہے تو منتقلی کی وجہ سے صرف ضائع نہیں ہوتا ہے۔ A. مقابلے میں کچھ بھی ہو سکتا ہے۔ جیسا کہ بہت سے مبصرین نے پریشان ہونے کے بعد کہا ہے، "اسی لیے وہ گیم کھیلتے ہیں۔"

اور اسی لیے ہم ریاضی سے کھیلتے ہیں۔ یہ تلاش کرنے کے لیے کہ کیا مزہ، اور مجبور، اور حیران کن ہے۔ کچھ بھی ہو سکتا ہے۔

مشقیں

1. فرض کریں کہ دو کھلاڑی دو طرفہ سکوں کا کھیل کھیلتے ہیں، اور دو سکوں کے چار نمبر مختلف ہیں۔ بنیادی طور پر صرف چھ ممکنہ منظرنامے ہیں کہ کون جیتتا ہے اور کتنی بار۔ وہ کیا ہیں؟

2. اوپر بیان کردہ تین رخی کھیل کے منظر نامے میں، اس کے لیے ایک مختلف تین رخی سکہ تلاش کریں۔ C تاکہ B کے خلاف اب بھی پسند کیا جاتا ہے C اور C کے خلاف اب بھی پسند کیا جاتا ہے A.

3. ثابت کریں کہ سکوں کے دو رخی کھیل میں تین کھلاڑیوں کا ہونا ناممکن ہے A, B, C اس طرح کہ A کے خلاف پسند کیا جاتا ہے۔ B, B کے خلاف پسند کیا جاتا ہے۔ C، اور C کے خلاف پسند کیا جاتا ہے۔ A.