1ICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Castelldefels, Spain
2CFIS-Centre de Formació Interdisciplinària Superior, UPC-Universitat Politècnica de Catalunya, 08028 Barcelona, Spain
3Univ Grenoble Alpes, CNRS, Grenoble INP, Institut Néel, 38000 Grenoble, France
4ICREA-Institucio Catalana de Recerca i Estudis Avançats, Lluis Companys 23, 08010 Barcelona, Spain
اس کاغذ کو دلچسپ لگتا ہے یا اس پر بات کرنا چاہتے ہیں؟ SciRate پر تبصرہ کریں یا چھوڑیں۔.
خلاصہ
باہمی غیرجانبدار بنیادیں کوانٹم انفارمیشن تھیوری میں پیمائش کے انتہائی مفید جوڑوں کے مساوی ہیں۔ سب سے چھوٹی جامع جہت، چھ میں، یہ معلوم ہوتا ہے کہ تین سے سات کے درمیان باہمی طور پر غیرجانبدار بنیادیں موجود ہیں، جن میں دہائیوں پرانا قیاس ہے، جسے زاؤنر کے قیاس کے نام سے جانا جاتا ہے، یہ بتاتے ہوئے کہ زیادہ سے زیادہ تین موجود ہیں۔ یہاں ہم زاؤنر کے قیاس کو عددی طور پر ہر جوڑے کے عدد $n,d ge 2$ کے لیے بیل عدم مساوات کی تعمیر کے ذریعے حل کرتے ہیں جس کی زیادہ سے زیادہ خلاف ورزی $d$ کی جا سکتی ہے اگر اور صرف اس صورت میں جب $n$ MUBs اس جہت میں موجود ہوں۔ اس لیے ہم زاؤنر کے قیاس کو ایک اصلاحی مسئلہ میں بدل دیتے ہیں، جسے ہم تین عددی طریقوں سے حل کرتے ہیں: see-saw optimization، non-linear semidefinite programming اور Monte Carlo تکنیک۔ تینوں طریقے کم جہتوں میں معلوم معاملات کی درست شناخت کرتے ہیں اور سبھی تجویز کرتے ہیں کہ طول و عرض چھ میں چار باہمی غیرجانبدار اڈے موجود نہیں ہیں، ان تمام اڈوں کو تلاش کرنے کے ساتھ جو عددی طور پر متعلقہ بیل عدم مساوات کو بہتر بناتے ہیں۔ مزید برآں، یہ عددی اصلاح کرنے والے طول و عرض چھ میں "چار سب سے دور دراز اڈوں" کے ساتھ موافق نظر آتے ہیں، جو کہ [P. Raynal, X. Lü, B.-G. اینگلرٹ، {فز۔ Rev. A}، {83} 062303 (2011)]۔ آخر میں، مونٹی کارلو کے نتائج بتاتے ہیں کہ زیادہ سے زیادہ تین MUBs طول و عرض دس میں موجود ہیں۔
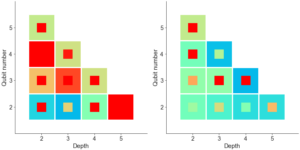
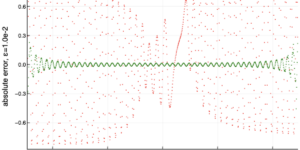
نمایاں تصویر: ہماری بیل کی عدم مساوات کی قدر کے درمیان نسبتا فرق یہ فرض کرتے ہوئے کہ n MUBs طول و عرض d میں موجود ہیں اور ہمارے عددی طریقوں سے پائی جانے والی قدر۔ صفر کی قدروں کا مطلب ہے کہ طریقے n MUBs کو طول و عرض d میں پائے گئے، جب کہ غیر صفر اقدار کا مطلب ہے کہ طریقوں نے n MUBs کو طول و عرض d میں نہیں پایا۔ تمام معلوم صورتوں (جہت دو سے پانچ اور طول و عرض چھ دو اور تین MUBs کے ساتھ) کو اعداد کے ذریعہ صحیح طریقے سے شناخت کیا گیا ہے۔ طول و عرض چھ میں، کوئی بھی طریقہ چار MUB نہیں ڈھونڈتا ہے، اور تمام طریقے چار اڈوں کے ایک ہی سیٹ پر اکٹھے ہوتے ہیں۔
مقبول خلاصہ
ان کے وسیع استعمال کے باوجود، MUBs کے ڈھانچے کے بارے میں اب بھی کھلے سوالات باقی ہیں۔ سب سے نمایاں طور پر، پیمائش کی زیادہ سے زیادہ تعداد جو جوڑے کے لحاظ سے غیر جانبدار ہے ("MUBs کی تعداد") نامعلوم ہے اگر کوانٹم سسٹم کا طول و عرض ایک جامع نمبر ہے۔ خاص طور پر، طول و عرض چھ میں ہم صرف یہ جانتے ہیں کہ MUBs کی تعداد تین سے سات کے درمیان ہے۔ ایک طویل عرصے سے کھلا قیاس زاؤنر کا ہے، جس میں کہا گیا ہے کہ طول و عرض چھ میں تین سے زیادہ MUB موجود نہیں ہیں۔ دہائیوں پر محیط اس قیاس کو کچھ عددی شواہد کی حمایت حاصل ہے، لیکن آج تک اس کا کوئی ثبوت موجود نہیں ہے۔
اس کام میں ہم بیل نان لوکلٹی کے ذریعے زاؤنر کے قیاس سے نمٹتے ہیں۔ بیل نان لوکلٹی دو تجربہ کاروں سے متعلق ہے جنہیں بات چیت کرنے کی اجازت نہیں ہے، لیکن وہ کلاسیکی بے ترتیب پن یا مشترکہ کوانٹم حالت کی شکل میں کچھ ارتباط کا اشتراک کر سکتے ہیں۔ یہ دکھایا گیا ہے کہ کوانٹم وسائل کا اشتراک تجرباتی اعداد و شمار کا باعث بن سکتا ہے جس کی وضاحت کلاسیکی طبیعیات (زیادہ واضح طور پر، نام نہاد مقامی پوشیدہ متغیر ماڈلز کے ذریعہ) کے ذریعہ نہیں کی جاسکتی ہے۔ یہ بیل کے نظریے کے نام سے جانا جاتا ہے، اور گزشتہ دہائی میں اس کی تجرباتی طور پر تصدیق کی گئی ہے۔ تجرباتی اعداد و شمار کے غیر کلاسیکی ہونے کا مشاہدہ عام طور پر نام نہاد بیل عدم مساوات کے ذریعے کیا جاتا ہے، جو تجربے میں ہونے والے پیمائش کے نتائج کے امکانات کے افعال ہیں۔ کلاسیکی ڈیٹا کو بیل کی عدم مساوات کو پورا کرنا چاہیے، جبکہ کوانٹم ڈیٹا ان کی خلاف ورزی کر سکتا ہے۔
حال ہی میں، بیل کی عدم مساواتیں پائی گئی ہیں جن کی زیادہ سے زیادہ خلاف ورزی ہوتی ہے اگر فریقین میں سے کوئی ایک دیے گئے جہت کے MUB پیمائش کے جوڑے کو ملازمت دیتا ہے۔ اس کام میں، ہم ان عدم مساوات کو نئی تک بڑھاتے ہیں، جس کی زیادہ سے زیادہ خلاف ورزی کسی مخصوص جہت میں MUB پیمائش کی منتخب تعداد سے ہوتی ہے۔ مزید برآں، اگر تجربے میں طول و عرض مقرر ہے، زیادہ سے زیادہ خلاف ورزی اس صورت میں حاصل کی جاتی ہے جب اور صرف اس صورت میں جب استعمال شدہ پیمائش دی گئی جہت میں MUBs کی منتخب کردہ تعداد کے مطابق ہو۔ لہذا، یہ فیصلہ کرنا کہ آیا کسی مخصوص جہت میں MUBs کی منتخب تعداد موجود ہے، اس مقررہ جہت میں متعلقہ بیل عدم مساوات کی زیادہ سے زیادہ خلاف ورزی کو تلاش کرنے کے مترادف ہے۔
اگرچہ اس زیادہ سے زیادہ خلاف ورزی کو تلاش کرنا عام طور پر ایک مشکل مسئلہ ہے، ہم اپنی بیل کی عدم مساوات کی زیادہ سے زیادہ خلاف ورزی کو ایک مقررہ جہت میں تلاش کرنے کی کوشش کے طور پر تین مختلف عددی طریقے استعمال کرتے ہیں۔ ان میں سے دو طریقے سیمی ڈیفائنٹ پروگرامنگ تکنیک کی مختلف قسمیں ہیں، جب کہ تیسرا طریقہ شماریاتی طبیعیات سے متاثر ہے اور اسے نقلی اینیلنگ کہا جاتا ہے۔ جب کہ یہ تمام طریقے تحقیقی ہیں- یعنی اس بات کی کوئی گارنٹی نہیں ہے کہ وہ مسئلے کی صحیح بہترین تلاش کر لیں گے- کوئی بھی ان کو اصلاحی مسائل پر لاگو کر کے ان کی کارکردگی کا اندازہ لگا سکتا ہے جن کا بہترین معلوم ہے۔ خاص طور پر، ہمیں معلوم ہوتا ہے کہ تینوں طریقے MUB پیمائشوں کو ان صورتوں میں شناخت کرنے کے قابل ہیں جہاں وہ موجود ہیں۔ مزید برآں، ان صورتوں میں جہاں ان کے موجود نہ ہونے کے بارے میں جانا جاتا ہے، تینوں طریقے عددی درستگی تک پیمائش کے ایک ہی سیٹ میں بدل جاتے ہیں۔ اس کے بعد ہم اپنے طریقوں کو پہلے نامعلوم کیس پر لاگو کرتے ہیں، یعنی چھ جہت میں چار MUBs۔ طریقوں میں سے کوئی بھی طول و عرض چھ میں چار MUBs کی شناخت کرنے کے قابل نہیں ہے، لیکن پھر وہ تمام چار پیمائشوں کے ایک ہی سیٹ میں عددی درستگی تک جمع ہو جاتے ہیں۔ مزید برآں، مصنوعی اینیلنگ تکنیک کو اگلے جامع جہت، طول و عرض دس میں چار MUB نہیں ملتے ہیں۔ لہٰذا، اگرچہ ہماری تکنیک کی تحقیقی نوعیت کی وجہ سے سخت دعوے نہیں کیے جا سکتے، ہمارے نتائج بیل غیر مقامیت کے نئے تناظر سے زاؤنر کے قیاس کی تائید کرتے ہیں۔
► BibTeX ڈیٹا
► حوالہ جات
ہے [1] آئی ڈی Ivanovic. کوانٹل حالت کے تعین کی ہندسی وضاحت۔ طبیعیات کا جریدہ A: ریاضی اور عمومی، 14(12):3241–3245، 1981. doi:10.1088/0305-4470/14/12/019۔
https://doi.org/10.1088/0305-4470/14/12/019
ہے [2] جی براسارڈ سی ایچ بینیٹ۔ کوانٹم کرپٹوگرافی: عوامی کلید کی تقسیم اور سکے پھینکنا۔ کمپیوٹرز، سسٹمز اور سگنل پروسیسنگ پر IEEE بین الاقوامی کانفرنس کی کارروائی (IEEE، 1984)، 175:8، 1984. doi:10.1016/j.tcs.2011.08.039.
https://doi.org/10.1016/j.tcs.2011.08.039
ہے [3] Artur K. Ekert. بیل کے تھیوریم پر مبنی کوانٹم کرپٹوگرافی۔ طبیعیات Rev. Lett., 67:661–663, 1991. doi:10.1103/ PhysRevLett.67.661.
https:///doi.org/10.1103/PhysRevLett.67.661
ہے [4] ڈگمار بروس۔ چھ ریاستوں کے ساتھ کوانٹم کرپٹوگرافی میں بہترین چھان بین۔ طبیعات Rev. Lett., 81:3018–3021, 1998. doi:10.1103/ PhysRevLett.81.3018.
https:///doi.org/10.1103/PhysRevLett.81.3018
ہے [5] ارمین تاواکولی، ایلی حمیدی، برینو مارکیز، اور محمد بورینانے۔ واحد $d$-سطح کے نظاموں کا استعمال کرتے ہوئے کوانٹم بے ترتیب رسائی کوڈز۔ طبیعیات Rev. Lett., 114:170502, 2015. doi:10.1103/ PhysRevLett.114.170502.
https:///doi.org/10.1103/PhysRevLett.114.170502
ہے [6] Máté Farkas اور Jędrzej Kaniewski۔ تیاری اور پیمائش کے منظر نامے میں باہمی غیر جانبدارانہ بنیادوں کی خود جانچ۔ طبیعات Rev. A, 99:032316, 2019. doi:10.1103/ PhysRevA.99.032316.
https:///doi.org/10.1103/PhysRevA.99.032316
ہے [7] H. Bechmann-Pasquinucci اور N. Gisin. بائنری پیمائش کے ساتھ قونٹس کے لیے بیل کی عدم مساوات۔ کوانٹم معلومات۔ Comput., 3(2):157–164, 2003. doi:10.26421/QIC3.2-6.
https://doi.org/10.26421/QIC3.2-6
ہے [8] Jędrzej Kaniewski، Ivan Šupić، Jordi Tura، Flavio Baccari، Alexia Salavrakos، اور Remigiusz Augusiak۔ زیادہ سے زیادہ الجھاؤ اور باہمی غیرجانبدار اڈوں سے زیادہ سے زیادہ غیر مقامییت، اور دو کوٹرٹ کوانٹم سسٹمز کی خود جانچ۔ کوانٹم، 3:198، 2019۔ doi:10.22331/q-2019-10-24-198۔
https://doi.org/10.22331/q-2019-10-24-198
ہے [9] ارمین تاواکولی، میٹی فارکاس، ڈینس روزیٹ، ژان ڈینیئل بنکل، اور جیڈرزیج کینیوسکی۔ بیل تجربات میں باہمی طور پر غیر جانبدارانہ بنیادیں اور ہم آہنگ معلوماتی طور پر مکمل پیمائش۔ سائنس ایڈوانسز، 7(7):eabc3847, 2021. doi:10.1126/sciadv.abc3847۔
https://doi.org/10.1126/sciadv.abc3847
ہے [10] Thomas Durt، Berthold-Georg Englert، Ingemar Bengtsson، اور Karol Życzkowski۔ باہمی غیر جانبدارانہ بنیادوں پر۔ انٹرنیشنل جرنل آف کوانٹم انفارمیشن، 08(04):535–640، 2010. doi:10.1142/S0219749910006502۔
https:///doi.org/10.1142/S0219749910006502
ہے [11] ولیم کے ووٹرز اور برائن ڈی فیلڈز۔ باہمی غیرجانبدارانہ پیمائش کے ذریعے بہترین ریاست کا تعین۔ طبیعیات کی تاریخ، 191(2):363–381، 1989. doi:10.1016/0003-4916(89)90322-9۔
https://doi.org/10.1016/0003-4916(89)90322-9
ہے [12] پاول ووکجان اور تھامس بیتھ۔ مربع طول و عرض میں باہمی غیرجانبدار اڈوں کی نئی تعمیر۔ کوانٹم معلومات۔ Comput., 5(2):93–101, 2005. doi:10.26421/QIC5.2-1۔
https://doi.org/10.26421/QIC5.2-1
ہے [13] میہلی وینر۔ باہمی غیرجانبدار اڈوں کی زیادہ سے زیادہ تعداد کے لیے ایک خلا۔ پروک عامر ریاضی Soc., 141:1963–1969, 2013. doi:10.1090/S0002-9939-2013-11487-5۔
https://doi.org/10.1090/S0002-9939-2013-11487-5
ہے [14] گیرہارڈ زونر۔ کوانٹینڈیزائنز: Grundzüge einer nichtkommutativen Designtheorie۔ پی ایچ ڈی کا مقالہ، 1999۔
ہے [15] P. آسکر بوائکن، میرا سیتارام، فام ہوو ٹیپ، اور پاول ووکجان۔ جھوٹ الجبرا کے باہمی طور پر غیرجانبدار اڈے اور آرتھوگونل سڑن۔ کوانٹم معلومات۔ Comput., 7(4):371–382, 2007. doi:10.26421/QIC7.4-6.
https://doi.org/10.26421/QIC7.4-6
ہے [16] اسٹیفن بریرلی اور اسٹیفن ویگرٹ۔ طول و عرض چھ میں باہمی طور پر غیر جانبدار بنیادوں کی تعمیر۔ طبیعیات Rev. A, 79:052316, 2009. doi:10.1103/ PhysRevA.79.052316.
https:///doi.org/10.1103/PhysRevA.79.052316
ہے [17] Philippe Jaming، Máté Matolcsi، Péter Móra، Ferenc Szöllősi، اور Mihály Weiner۔ پاؤلی کا ایک عمومی مسئلہ اور طول و عرض میں MUB-ٹرپلٹس کا ایک لامحدود خاندان 6۔
https://doi.org/10.1088/1751-8113/42/24/245305
ہے [18] گیری میک کونل، ہیری اسپینسر، اور آفاق طاہر۔ $mathbb{C}^6$ میں Zauner کے MUB قیاس کے حق میں اور اس کے خلاف ثبوت۔ 2021. doi:10.48550/arXiv.2103.08703.
https://doi.org/10.48550/arXiv.2103.08703
ہے [19] سینڈر گربلنگ اور سوین پولک۔ باہمی طور پر غیرجانبدار بنیادیں: کثیر الجہتی اصلاح اور توازن۔ 2021. doi:10.48550/arXiv.2111.05698۔
https://doi.org/10.48550/arXiv.2111.05698
ہے [20] Ingemar Bengtsson، Wojciech Bruzda، Åsa Ericsson، Jan-Åke Larsson، Wojciech Tadej، اور Karol Życzkowski۔ باہمی طور پر غیرجانبدار اڈے اور ترتیب چھ کی حدمرد میٹرکس۔ جرنل آف میتھمیٹیکل فزکس، 48(5):052106، 2007. doi:10.1063/1.2716990۔
https://doi.org/10.1063/1.2716990
ہے [21] Philippe Raynal، Xin Lü، اور Berthold-Georg Englert۔ چھ جہتوں میں باہمی طور پر غیرجانبدار اڈے: چار سب سے زیادہ دور کی بنیاد۔ طبیعات Rev. A, 83:062303, 2011. doi:10.1103/ PhysRevA.83.062303.
https:///doi.org/10.1103/PhysRevA.83.062303
ہے [22] Edgar A. Aguilar، Jakub J. Borkała، Piotr Mironowicz، اور Marcin Pawłowski۔ باہمی غیر جانبدارانہ اڈوں اور کوانٹم بے ترتیب رسائی کوڈز کے درمیان رابطے۔ طبیعیات Rev. Lett., 121:050501, 2018. doi:10.1103/physRevLett.121.050501.
https:///doi.org/10.1103/PhysRevLett.121.050501
ہے [23] نکولس برنر، ڈینیئل کیولکانٹی، سٹیفانو پیرونی، ویلریو سکارانی، اور سٹیفنی ویہنر۔ بیل نان لوکلٹی۔ Rev. Mod طبیعیات، 86:419–478، 2014. doi:10.1103/RevModPhys.86.419.
https:///doi.org/10.1103/RevModPhys.86.419
ہے [24] MOSEK ApS MOSEK فیوژن API برائے C++ 9.2.49، 2021۔ URL: https:///docs.mosek.com/9.2/cxxfusion/index.html۔
https:///docs.mosek.com/9.2/cxxfusion/index.html
ہے [25] ہیروشی یاماشیتا، ہیروشی یابے، اور کوہی ہارڈا۔ غیر لکیری سیمی ڈیفائنیٹ پروگرامنگ کے لیے ایک بنیادی – دوہری اندرونی نقطہ کا طریقہ۔ ریاضیاتی پروگرامنگ، 135(1):89–121، 2012. doi:10.1007/s10107-011-0449-z.
https://doi.org/10.1007/s10107-011-0449-z
ہے [26] اسٹیفن بائیڈ اور لیون وینڈنبرگ۔ محدب اصلاح۔ کیمبرج یونیورسٹی پریس، 2004. doi: 10.1017/CBO9780511804441۔
https://doi.org/10.1017/CBO9780511804441
ہے [27] ایس کرک پیٹرک، سی ڈی جیلاٹ، اور ایم پی ویچی۔ نقلی اینیلنگ کے ذریعہ اصلاح۔ سائنس، 220(4598):671–680، 1983. doi:10.1126/science.220.4598.671.
https://doi.org/10.1126/science.220.4598.671
ہے [28] نکولس میٹروپولیس، اریانا ڈبلیو روزن بلوتھ، مارشل این روزن بلوتھ، آگسٹا ایچ ٹیلر، اور ایڈورڈ ٹیلر۔ فاسٹ کمپیوٹنگ مشینوں کے ذریعے ریاستی حسابات کی مساوات۔ جرنل آف کیمیکل فزکس، 21(6):1087–1092، 1953. doi:10.1063/1.1699114۔
https://doi.org/10.1063/1.1699114
ہے [29] Miguel Navascués، Stefano Pironio، اور Antonio Acín. کوانٹم ارتباط کے سیٹ کو باؤنڈنگ کرنا۔ طبیعات Rev. Lett., 98:010401, 2007. doi:10.1103/ PhysRevLett.98.010401.
https:///doi.org/10.1103/PhysRevLett.98.010401
کی طرف سے حوالہ دیا گیا
یہ مقالہ کوانٹم میں کے تحت شائع کیا گیا ہے۔ Creative Commons انتساب 4.0 انٹرنیشنل (CC BY 4.0) لائسنس کاپی رائٹ اصل کاپی رائٹ ہولڈرز جیسے مصنفین یا ان کے اداروں کے پاس رہتا ہے۔