Tam giác nhỏ nhất lớn nhất vừa nhỏ hơn | Tạp chí Quanta

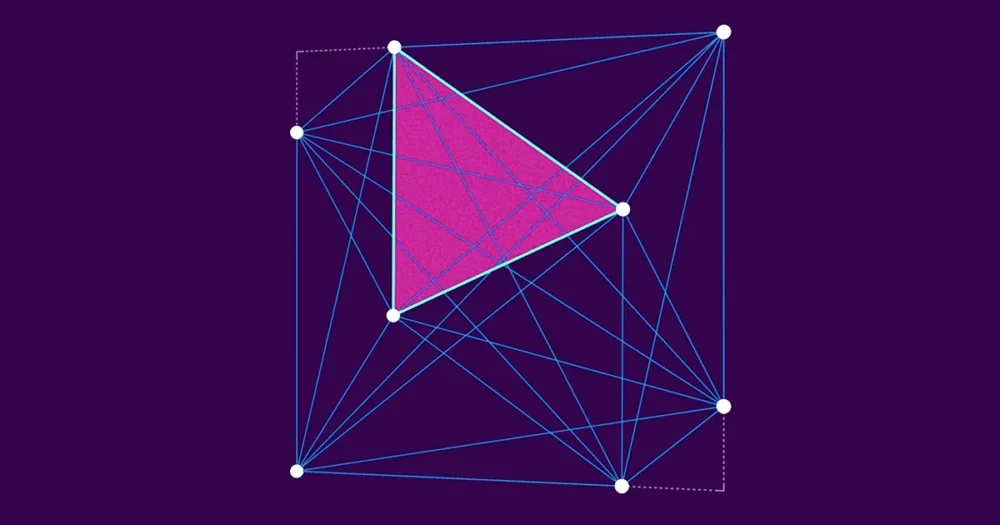
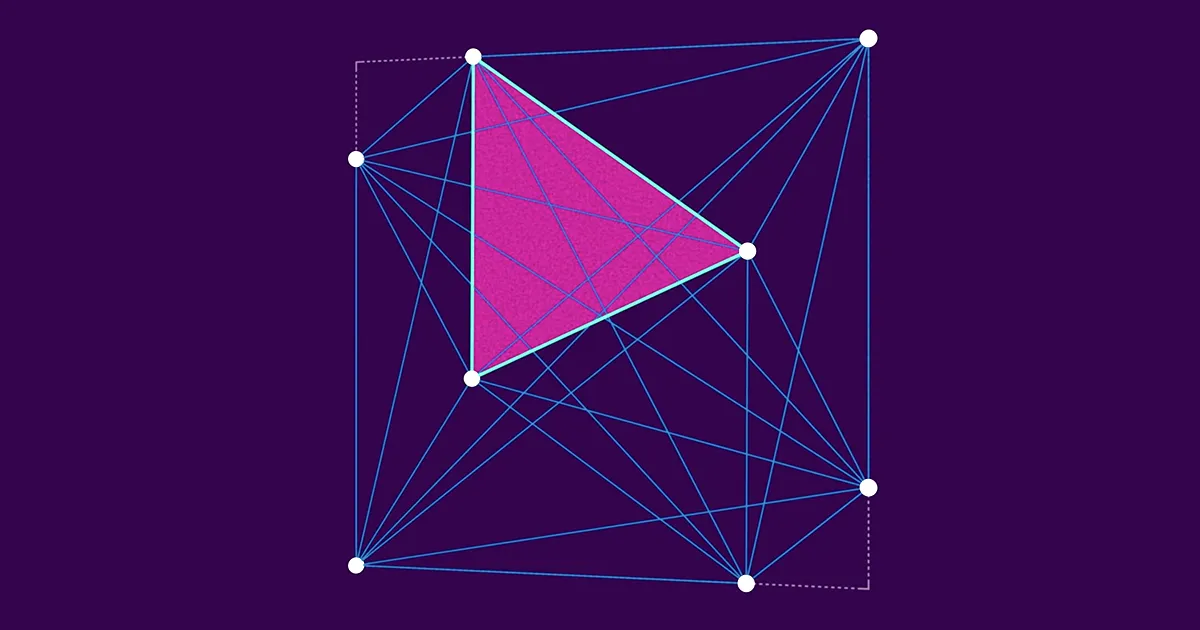
Hãy xem xét một hình vuông có nhiều điểm bên trong. Lấy ba điểm đó và bạn có thể tạo thành một hình tam giác. Bốn điểm xác định bốn hình tam giác khác nhau. Mười điểm xác định 120 hình tam giác. Các con số tăng lên nhanh chóng từ đó - 100 điểm xác định 161,700 hình tam giác khác nhau. Tất nhiên, mỗi hình tam giác đó có một diện tích cụ thể.

Hans Heilbronn, một nhà toán học người Đức trốn khỏi đất nước trước Thế chiến thứ hai và định cư ở Anh, đã nghĩ đến những hình tam giác này vào cuối những năm 1940 khi ông nhìn thấy một nhóm binh lính bên ngoài cửa sổ phòng mình. Những người lính dường như không theo đội hình, điều này khiến anh nghĩ: Nếu có n những người lính bên trong một hình vuông, kích thước của hình tam giác nhỏ nhất có thể lớn nhất được xác định bởi ba người trong số họ là bao nhiêu? Heilbronn tự hỏi làm thế nào người ta có thể sắp xếp các quân lính (hoặc, để đơn giản về mặt toán học, các điểm) để tối đa hóa kích thước của hình tam giác nhỏ nhất.

Vấn đề được phát biểu rất đơn giản, nhưng tiến trình giải quyết bài toán tam giác Heilbronn, như tên gọi của nó, đã bị đình trệ và kết quả hoàn toàn cạn kiệt vào những năm 1980. Rồi tháng XNUMX vừa qua, ba nhà toán học -- Alex Cohen, Cosmin Pohoata và Dmitrii Zakharov - đã công bố một nón mới về kích thước của hình tam giác nhỏ nhất. “Tôi nghĩ đó là một kết quả đáng kinh ngạc,” Anthony Carbery, một nhà toán học tại Đại học Edinburgh, nói.

Các nhà nghiên cứu vẫn tiếp tục nghiên cứu bài toán tam giác Heilbronn trong nhiều năm, bất chấp sự chờ đợi lâu dài để đạt được tiến bộ, được thúc đẩy bởi sự liên kết rối rắm của nó với các lĩnh vực toán học khác. Pohoata, giáo sư tại Đại học Emory ở Atlanta cho biết: “Những thứ được kết nối để khiến nó trở nên sống động”. Nó liên quan chặt chẽ đến các bài toán về các hình giao nhau, từ đó kết nối với cả lý thuyết số và phân tích Fourier - nghiên cứu về các hàm phức tạp được xây dựng từ các sóng đơn giản.

Cohen, một sinh viên tốt nghiệp tại Viện Công nghệ Massachusetts, tình cờ biết được mạng lưới kết nối này vào năm ngoái. Anh đang đọc lại một bản khảo sát cũ về vấn đề tam giác Heilbronn của Klaus Roth, một người tị nạn khác từ Đức Quốc xã đã trốn sang Anh khi còn là một cậu bé. (Roth, qua đời năm 2015, là nhà toán học người Anh đầu tiên giành được Huy chương Fields.)

Cohen hình dung những ý tưởng từ cuộc khảo sát của Roth bằng một bức tranh đơn giản: một hình vuông được đan chéo bởi hai dải dày, với một đường mảnh ở giữa mỗi dải. Khi nghiên cứu sơ đồ của mình, Cohen nhận ra rằng nó có thể liên quan đến những ý tưởng mà cố vấn của ông, Larry Guth, đã đưa ra trong một cuộc họp nhóm đọc gần đây. Nhưng Guth chưa hề nói về hình tam giác.

Cohen nói: “Tôi nhanh chóng nhận ra rằng hai phương pháp này về cơ bản là tương đương nhau. “Tôi thực sự hào hứng với bài toán tam giác.”

Một ngày nọ, trong phòng sinh hoạt chung khoa toán của MIT, Cohen bất ngờ phát hiện ra rằng Pohoata, người đến để nói chuyện, và Zakharov, một sinh viên tốt nghiệp tại MIT, cũng đang nghiên cứu bài toán tam giác Heilbronn. Hơn nữa, họ đã tìm thấy cùng một liên kết. Ba người bắt đầu hợp tác. Bảy tháng sau, họ đã đạt được bước đột phá. Bài báo của họ thậm chí còn mang lại nhiều lĩnh vực toán học mới hơn. Thomas Bloom của Đại học Oxford cho biết: “Họ sử dụng một lượng lớn máy móc và những hiểu biết khác nhau”. Ông hy vọng bài báo mới sẽ “thúc đẩy một thời kỳ phục hưng” về tiến bộ trong vấn đề tam giác.

Một giả thuyết bị loại bỏ

Bằng cách đặt ba điểm rất gần nhau, bạn có thể dễ dàng tạo ra hình tam giác nhỏ nhất theo cách sắp xếp nhỏ tùy ý. (Trong trường hợp cực đoan nhất, ba điểm thẳng hàng với nhau tạo thành một tam giác có diện tích bằng 1.) Nhưng cố gắng giữ cho tam giác nhỏ nhất lớn thì khó hơn. Khi bạn tiếp tục thêm nhiều dấu chấm hơn, hình tam giác nhỏ nhất buộc phải khá nhỏ - các dấu chấm mới chỉ có thể cách xa các dấu chấm hiện có. Tương đối dễ dàng chứng minh rằng tam giác nhỏ nhất không thể có diện tích lớn hơn XNUMX/(n − 2) bằng cách chia hình vuông thành các hình tam giác không chồng lên nhau.

Nhưng Heilbronn nghĩ rằng giới hạn đó thậm chí còn nhỏ hơn thế. Anh đoán rằng dù các chấm được sắp xếp như thế nào trong hình vuông thì cũng không thể có một hình tam giác nhỏ nhất có diện tích lớn hơn khoảng 1/n², một con số co lại nhanh hơn nhiều n mọc.

Hắn sai rồi.

Năm 1980, các nhà toán học Hungary János Komlós, János Pintz và Endre Szemerédi đã tìm thấy một mẫu số chấm có tam giác nhỏ nhất có diện tích lớn hơn 1/n². Trong một bài báo riêng xuất bản cùng thời điểm, họ cũng chỉ ra rằng không thể sắp xếp n các dấu chấm để tạo một hình tam giác nhỏ nhất lớn hơn khoảng 1/n^8/7. Khi nào n lớn, giá trị này nhỏ hơn nhiều so với 1/n, nhưng lớn hơn nhiều so với 1/n².

Những kết quả đó đã tồn tại trong hơn 40 năm. Bloom cho biết: “Việc cải thiện [ràng buộc] theo một trong hai hướng cực kỳ khó khăn và đòi hỏi nhiều phân tích kỹ thuật cũng như sự khéo léo.

Carbery nói thêm: “Bạn rất nhanh chóng bị sa lầy bởi một vũng lầy đầy thứ.

Trong khi công trình được phát hiện vào năm 1980 vẫn là công trình có tam giác nhỏ nhất được biết đến thì Cohen, Pohoata và Zakharov, lần đầu tiên sau bốn thập kỷ, đã thành công trong việc hạ thấp giới hạn trên.

Tiến hóa hội tụ

Vào thời điểm gặp Cohen, Pohoata đã nghiên cứu bài toán tam giác Heilbronn được hai năm. Vào mùa hè năm 2020, anh ấy yêu cầu các sinh viên nghiên cứu mùa hè tại Đại học Yale nghiên cứu các phiên bản có chiều cao hơn của bài toán - ví dụ: thu hẹp các hình có thể tích nhỏ nhất lớn nhất xuất hiện giữa các chấm nằm rải rác trong một khối lập phương ba chiều.

Là một phần của dự án đó, Pohoata đã xem lại tất cả các công việc trước đây về vấn đề này. Trở lại trong 1951, Roth đã chia việc tìm kiếm các tam giác nhỏ thành hai phần: Đầu tiên tìm một cặp điểm để tạo thành đáy của tam giác, sau đó tìm điểm thứ ba để hoàn thành tam giác. Về cơ bản, chiến lược này định hình việc tìm kiếm một tam giác lớn nhỏ nhất như nghiên cứu về các dấu chấm và hình chữ nhật giao nhau - một phương pháp đã được cải tiến vào năm 1972 bởi Wolfgang Schmidt.

Khi đọc bài báo của Schmidt, Pohoata đã xác định được mối liên hệ với phương pháp cao-thấp - một kỹ thuật mà Guth và các cộng tác viên đã phát triển vào năm 2017 để ước tính sự chồng chéo giữa một tập hợp các dải hình chữ nhật và một tập hợp các đĩa. “Đó là một khoảnh khắc tâm lý quan trọng đối với tôi,” anh nói.

Năm 2021, Pohoata đưa ra ý tưởng của mình với Zakharov. Hai người đã bắt đầu xuất bản cùng nhau khi Zakharov vẫn còn là sinh viên đại học ở Moscow. Jacob Fox, một nhà toán học tại Đại học Stanford, cho biết: “[Zakharov] đã làm được những điều đáng chú ý như thể anh ấy là một nhà nghiên cứu cấp cao khi còn trẻ.

Zakharov ban đầu tỏ ra bi quan về bài toán tam giác Heilbronn. “Tôi đã nghĩ rằng, 8/7 này đã tồn tại ở đó suốt 40 năm, vậy tôi là ai mà có thể phá vỡ nó?” anh ấy nói. “Tôi chủ yếu muốn hiểu nó hoạt động như thế nào.”

Sau khi tình cờ gặp nhau vào tháng 2022 năm 8, Cohen, Pohoata và Zakharov đã sớm xác định được trở ngại mà Komlós, Pintz và Szemerédi đã vô tình phải đối mặt. Cohen nói: “Có một sự sắp xếp rất cụ thể về các điểm dẫn đến tình huống xấu nhất là họ không thể làm tốt hơn 7/XNUMX”. “Các điểm có thể tập trung hoặc dàn trải. Trường hợp xấu nhất là khi đó là sự kết hợp nào đó.” Sự sắp xếp đó có các điểm trải rộng trên quy mô lớn, nhưng nếu bạn phóng to các ô vuông nhỏ trong ô vuông đơn vị, bạn sẽ thấy các mẫu có trật tự.

Cohen, Pohoata và Zakharov nhận ra rằng họ có thể đạt được tiến bộ bằng cách nghiên cứu kích thước của các cụm điểm nhỏ. Đối với những người không chuyên về toán học, các kích thước luôn là số nguyên: Một tờ giấy có hai chiều; một viên gạch đất sét có ba chiều.

Mọi thứ có thể trở nên kỳ lạ khi bạn xem xét thứ nguyên của một tập hợp điểm. Một điểm thường được coi là không chiều. Nhưng hai tập hợp điểm hữu hạn có thể có cấu trúc hoàn toàn khác nhau. Một người có thể có 10 điểm ngoan ngoãn đi theo một đường thẳng, trong khi người kia có 10 điểm rải rác trên toàn bộ hình vuông đơn vị.

Để nắm bắt được cấu trúc của những tập hợp điểm kỳ lạ nhất, nhà toán học đầu thế kỷ 20 Felix Hausdorff đã đưa ra một khái niệm mới về chiều. Theo định nghĩa này, 10 điểm trên một đường thẳng là một chiều, trong khi 10 điểm trải đều trên một hình vuông là hai chiều. Nhưng trong thế giới này, các chiều không nhất thiết phải là số nguyên và tập hợp một chiều không thể là tuyến tính mà là fractal, thể hiện vô số lớp mẫu phức tạp. Tùy thuộc vào chi tiết của các mẫu này, tập hợp điểm thậm chí có thể có thứ nguyên lớn hơn 0 nhưng nhỏ hơn 1.

Cohen, Pohoata và Zakharov đã khám phá ra một định lý 1953 của John Marstrand đã diễn đạt lại ước tính của Komlós, Pintz và Szemerédi theo chiều Hausdorff - nhưng chỉ với các chiều lớn hơn 1. Để cải thiện ước tính, Cohen, Pohoata và Zakharov cần tìm cách nào đó để tổng quát hóa kết quả của Marstrand thành các tập hợp có số chiều nhỏ hơn 1.

Tạo kết nối

Cohen, Pohoata và Zakharov không phải suy nghĩ lâu. Khi chuyện đó xảy ra, một bài báo của Khối u Orponen, Pablo Shmerkin và Hồng Vương điều đó vừa mới xảy ra Đăng trực tuyến đã mở rộng định lý 70 năm tuổi của Marstrand cho các tập hợp có số chiều nhỏ hơn 1.

Cohen đã không biết về bài báo cho đến tháng Hai. Sau khi làm vậy, anh ấy nhanh chóng chuyển nó cho Pohoata và Zakharov. Đến cuối tháng XNUMX, họ đã đăng bài báo của mình lên mạng, chứng minh rằng tam giác nhỏ nhất trong số n số điểm trong một hình vuông đơn vị không bao giờ có thể lớn hơn 1/n^{8 / 7 + 1 / 2000}.

Shmerkin bất chợt đọc tờ báo hình tam giác sau khi thấy nó được công bố trên Twitter. Trước đó, anh ấy thậm chí còn chưa biết đến bài toán tam giác Heilbronn, vì vậy anh ấy rất ngạc nhiên khi phát hiện ra sự liên quan đến chứng minh của mình. “Đây không phải là ứng dụng trực tiếp những gì chúng tôi làm. Có rất nhiều công việc sâu sắc, sáng tạo và kỹ thuật trong đó,” ông nói. “Đối với tôi, đó là một cảm giác tuyệt vời.”

Bloom cũng rất ấn tượng. “Lẽ ra tôi có thể xem bài báo đó rất lâu và không bao giờ nghĩ, ồ, điều này áp dụng được cho bài toán tam giác.”

Trong khi kết quả mới cải thiện số mũ của Komlós, Pintz và Szemerédi chỉ một phần rất nhỏ, nó đã làm sống lại bài toán tam giác Heilbronn đã tồn tại từ lâu. “Bạn có thể nhìn vào nó và nói, ngáp, ngáp, ngáp, nó trông không khác lắm so với những gì được biết đến vào năm 1982. Nhưng đã có rất nhiều thời gian trôi qua kể từ năm 1982,” Carbery nói.

Bằng cách kết hợp phương pháp cao-thấp và công trình của Orponen, Shmerkin và Wang, Cohen, Pohoata và Zakharov đã làm sáng tỏ một loạt mối liên hệ mới giữa bài toán tam giác Heilbronn và phần còn lại của toán học. Như Bloom đã nói, bài toán tam giác được coi là “một bài toán thực sự hay, thực sự khó mà chúng ta không biết phải làm gì. Nhưng họ nói rằng nó có liên quan đến rất nhiều thứ khác.”

Một số người tin rằng đáp án thực sự cho bài toán tam giác Heilbronn sẽ không lớn hơn nhiều so với dự đoán ban đầu của ông về 1/n². “Nếu tôi chấm điểm một cách có hệ thống thì tôi sẽ thất bại; nếu tôi cho điểm một cách ngẫu nhiên thì tôi sẽ thất bại. Nó không thể có cấu trúc quá chặt chẽ, không thể quá ngẫu nhiên, do đó nó có thể không tồn tại”, Bloom nói. Nhưng Zakharov đang hy vọng một câu trả lời khác. Trực giác ủng hộ câu trả lời 1/n² là "loại nhàm chán," ông nói. “Tôi rất thích nếu nó được n^3/2".