扰动参数量子演化导数的“本征”平移规则

扰动参数量子演化导数的“本征”平移规则

时间戳：11年2023月5日上午48:XNUMX

德克·奥利弗·泰斯

理论计算机科学，塔尔图大学，爱沙尼亚

觉得本文有趣或想讨论？ 在SciRate上发表评论或发表评论.

抽象

Banchi 和 Crooks（Quantum，2021）给出了根据通过我们所谓的“扰动”量子演化 $xmapsto e^{i(x A + B)/hbar}$ 输入的参数来估计期望值导数的方法。 他们的方法需要对出现的酉进行修改，而不仅仅是改变参数。 此外，在 $B$ 项不可避免的情况下，似乎没有已知导数的精确方法（无偏估计量）：Banchi & Crooks 的方法给出了近似值。
在本文中，为了估计这种类型的参数化期望值的导数，我们提出了一种只需要移动参数的方法，不需要对量子演化进行其他修改（“适当的”移动规则）。 我们的方法是精确的（即，它给出解析导数、无偏估计），并且具有与 Banchi-Crooks 相同的最坏情况方差。
此外，我们基于扰动参数量子演化的傅里叶分析，讨论了围绕固有移位规则的理论，从而根据傅里叶变换来表征固有移位规则，这反过来又导致我们得出不存在固有移位规则的结果。具有指数集中移位的移位规则。 我们推导出显示近似误差的截断方法，并与基于初步数值模拟的 Banchi-Crooks 方法进行比较。

扰动参数量子演化导数的“适当”转变规则 PlatoBlockchain 数据智能。垂直搜索。人工智能。

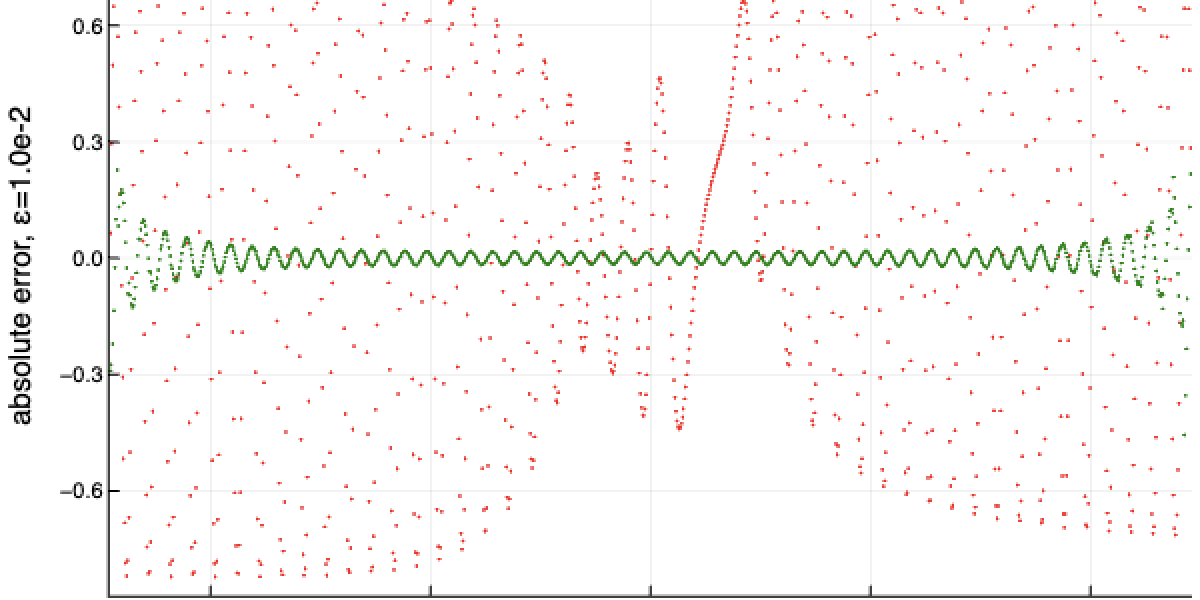
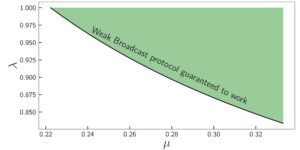
特色图片：初步数值结果表明新方法优于现有技术。 这是一张图，显示了对于一个随机选择的参数化量子演化，估计垂直方向导数的误差（偏差）和水平方向参数值。 绿点表示新方法的错误，红点表示最新方法。 （两种方法的其他性能变量都是固定的并且相同。）

热门摘要

在尝试使用当前或不久的将来的量子设备进行有意义的计算时，变分混合量子经典方法受到广泛采用。 它包括对量子演化进行参数化，然后在循环中优化这些参数，在量子计算和经典计算之间交替。

另一种方法是将计算问题映射到可以在量子硬件上实现的哈密顿量。 例如，为了对冷原子量子器件上的最大稳定集问题进行建模，里德堡封锁可以作为部分实现稳定性约束的一种方法。

当然，人们正在尝试将这两种方法结合起来。

为了优化参数，变分方法通常采用梯度估计器，并且这些估计器应该具有小偏差和小方差。 在数字量子计算世界中——即包含（参数化）门的量子电路——估计梯度是很好理解的，并且基于所谓的 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟 𝑠ℎ𝑖𝑓𝑡 𝑟𝑢𝑙𝑒𝑠。 但当数字与模拟结合时，会出现哈密顿量的参数化部分与其他部分不互通的情况。
考虑选择拉比频率作为参数之一，例如在里德伯原子阵列中局部到单个原子：拉比项不与里德伯封锁项交换。 还有更多的例子。 在这些情况下，已知的移位规则理论就失效了。
在我们的论文中，我们提出了一种估计这些情况的导数的新方法。 我们的方法沿着已知的移位规则范例工作，并在减少估计器偏差方面改进了现有技术。

►BibTeX数据

►参考

[1] Jarrod R McClean、Nicholas C Rubin、Joonho Lee、Matthew P Harrigan、Thomas E O'Brien、Ryan Babbush、William J Huggins 和 Hsin-Yuan Huang。 “量子计算机科学的基础教给我们关于化学的知识”。 化学物理杂志 155, 150901 (2021)。
https://doi.org/10.48550/arXiv.2106.03997

[2] Xiao Yuan、Suguru Endo、Qi Zhao、Ying Li 和 Simon C Benjamin。 “变分量子模拟理论”。 量子 3, 191 (2019)。
https://doi.org/10.48550/arXiv.1812.08767

[3] 御手洗浩介、根五郎真、喜多川正宏、藤井圭介。 “量子电路学习”。 物理。 修订版 A 98, 032309 (2018)。
https：/ / doi.org/ 10.1103 / PhysRevA.98.032309

[4] Marcello Benedetti、Erika Lloyd、Stefan Sack 和 Mattia Fiorentini。 “作为机器学习模型的参数化量子电路”。 量子科学与技术 4, 043001 (2019).
https:/​/​doi.org/​10.1088/​2058-9565/​ab4eb5

[5] 爱德华·法尔希、杰弗里·戈德斯通和萨姆·古特曼。 “一种量子近似优化算法”。 预印本（2014）。
https://doi.org/10.48550/arXiv.1411.4028

[6] Eric R Anschuetz、Jonathan P Olson、Alán Aspuru-Guzik 和 Yudong Cao。 “变分量子因式分解”。 预印本（2018）。
https://doi.org/10.48550/arXiv.1808.08927

[7] 卡洛斯·布拉沃-普列托、瑞安·拉罗斯、马可·塞雷佐、伊吉特·苏巴西、卢卡斯·辛西奥和帕特里克·J·科尔斯。 “变分量子线性求解器”。 预印本（2019）。
https://doi.org/10.48550/arXiv.1909.05820

[8] 瑞安·巴布什和哈特穆特·内文。 “使用子逻辑控制训练量子演化”（2019）。 美国专利 10,275,717。

[9] Louis-Paul Henry、Slimane Thabet、Constantin Dalyac 和 Loïc Henriet。 “量子进化内核：具有可编程量子位阵列的图形机器学习”。 物理评论 A 104, 032416 (2021)。
https://doi.org/10.48550/arXiv.2107.03247

[10] 康斯坦丁·达利亚克、卢伊克·亨利特、伊曼纽尔·让德尔、沃尔夫冈·莱赫纳、西蒙·佩德里克斯、马克·波切龙和玛格丽塔·维什切泽罗娃。 “针对工业优化难题的量子方法。 电动汽车智能充电领域的案例研究”。 EPJ 量子技术 8, 12 (2021)。
https://doi.org/10.48550/arXiv.2012.14859

[11] 瑞安·斯韦克、弗雷德里克·王尔德、约翰内斯·迈耶、玛丽亚·舒尔德、保罗·K·费尔曼、巴泰勒米·梅纳德-皮加诺和詹斯·艾塞特。 “混合量子经典优化的随机梯度下降”。 量子 4, 314 (2020)。
https://doi.org/10.48550/arXiv.1910.01155

[12] 李军、杨晓东、彭新华、孙昌普。 “量子最优控制的混合量子经典方法”。 物理。 莱特牧师。 118, 150503 (2017)。
https：/ / doi.org/ 10.1103 / PhysRevLett.118.150503

[13] 莱昂纳多·班奇和加文·E·克鲁克斯。 “用随机参数移动规则测量一般量子演化的解析梯度”。 量子 5, 386 (2021)。
https:/​/​doi.org/​10.22331/​q-2021-01-25-386

[14] 理查德·P·费曼. “在量子电动力学中具有应用的算子微积分”。 物理评论 84, 108 (1951)。
https：/ / doi.org/ 10.1103 / PhysRev.84.108

[15] 拉尔夫·M·威尔科克斯. “量子物理学中的指数算子和参数微分”。 数学物理杂志 8, 962–982 (1967)。
https：/ / doi.org/10.1063/ 1.1705306

[16] 哈维尔·吉尔·维达尔和德克·奥利弗·泰斯。 “参数化量子电路的微积分”。 预印本（2018）。
https://doi.org/10.48550/arXiv.1812.06323

[17] David Wierichs、Josh Izaac、Cody Wang 和 Cedric Yen-Yu Lin。 “量子梯度的一般参数转移规则”。 预印本（2021）。
https://doi.org/10.48550/arXiv.2107.12390

[18] 德克·奥利弗·泰斯。 “变分量子电路导数的有限支持参数移位规则的最优性”。 预印本（2021）。
https://doi.org/10.48550/arXiv.2112.14669

[19] 迈克尔·里德和巴里·西蒙。 “现代数学物理方法II：傅里叶分析，自伴性”。 第 2 卷。学术出版社。 （1975）。

[20] Jarrod R McClean、Sergio Boixo、Vadim N Smelyanskiy、Ryan Babbush 和 Hartmut Neven。 “量子神经网络训练领域的贫瘠高原”。 自然通讯 9, 4812 (2018)。
https:/​/​doi.org/​10.1038/​s41467-018-07090-4

[21] Andrew Arrasmith、Zoë Holmes、Marco Cerezo 和 Patrick J Coles。 “量子贫瘠高原等同于成本集中和狭窄的峡谷”。 量子科学与技术 7, 045015 (2022).
https://doi.org/10.48550/arXiv.2104.05868

[22] 沃尔特·鲁丁. “泛函分析”。 麦格劳-希尔。 （1991）。

[23] 埃利亚斯·M·斯坦和拉米·沙卡奇。 “傅里叶分析：简介”。 第 1 卷。普林斯顿大学出版社。 （2011）。

[24] 杰拉尔德·B·福兰德. “抽象谐波分析课程”。 第 29 卷。CRC 出版社。 （2016）。

[25] 唐·扎吉尔. “双对数函数”。 数论、物理学和几何前沿 II。 第 3–65 页。 施普林格（2007）。

[26] 伦纳德·C·马克西蒙. “复数论证的双对数函数”。 伦敦皇家学会会刊。 A 系列：数学、物理和工程科学 459, 2807–2819 (2003)。
https：/ / doi.org/ 10.1098 / rspa.2003.1156

[27] 埃利亚斯·M·斯坦和拉米·沙卡奇。 “复杂分析”。 第 2 卷。普林斯顿大学出版社。 （2010）。

[28] 沃尔特·鲁丁. “真实和复杂的分析”。 麦格劳-希尔。 （1987）。

[29] 海因茨·鲍尔. “质量与整合理论”。 沃尔特·德·格鲁特. （1992）。 第二版。

[30] 弗朗茨·雷利希和约瑟夫·伯科维茨。 “特征值问题的微扰理论”。 CRC出版社。 （1969）。

被引用

[1] Roeland Wiersema、Dylan Lewis、David Wierichs、Juan Carrasquilla 和 Nathan Killoran，“$mathrm{SU}(N)$ 来了：多元量子门和梯度”， 的arXiv：2303.11355, (2023).

以上引用来自 SAO / NASA广告 （最近成功更新为2023-07-14 10:03:06）。 该列表可能不完整，因为并非所有发布者都提供合适且完整的引用数据。

On Crossref的引用服务 找不到有关引用作品的数据（上一次尝试2023-07-14 10:03:04）。

该论文发表在《量子》杂志上 国际知识共享署名署名4.0（CC BY 4.0） 执照。 版权归原始版权持有者所有，例如作者或其所在机构。

时间戳记：

更多来自 量子杂志