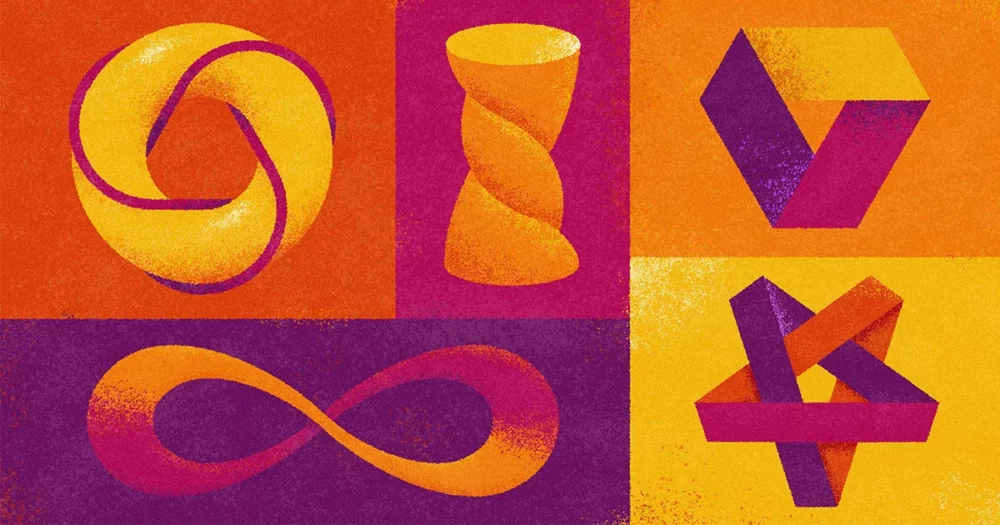Matematikere identificerer de bedste versioner af ikoniske former | Quanta Magasinet

I løbet af de sidste to år har matematikere identificeret de bedste versioner af et barns legeværelses former. Disse resultater indtager et skævt hjørne af matematikken og er passende nok frembragt af usandsynlige samarbejder, der involverer en matematiker, der praktiserer origami med sin kone, og en professor, der lærer hendes studerende at lege med papir.

Arbejdet foregår inden for studiet af "optimale" former, hvilket involverer at forstå, hvilken version af en form, der bedst opnår et mål givet nogle begrænsninger. Bier forstår dette implicit: De bygger honningkager med sekskantede celler, fordi sekskanter giver mest lagerkapacitet ved at bruge de færreste ressourcer.

I det mindste i lore var den første person, der søgte efter en sådan form, Dido, den grundlæggende dronning af Karthago. Efter at hun landede på det, der i dag er Tunesiens kyst, indgik hun en aftale med berberkongen Iarbas. Han gik med til at give hende det land, hun kunne indeslutte i et enkelt okseskjul. I stedet for at lægge det magre skjul fladt, som Iarbas havde forventet, skar Dido det i tynde strimler, som hun brugte til at omkranse og gøre krav på en hel bakke. Den opstigende dronnings indsigt var, at givet en fast mængde materiale, er den optimale områdeomsluttende form, som definerede Karthagos bygrænser, cirklen.

"De har normalt denne smag. Der er en familie af objekter, og du vil gerne vide, hvilken der maksimerer dette eller minimerer det," sagde Richard Schwartz fra Brown University, som postede tre resultater om optimale former i hurtig rækkefølge fra sidste august, inklusive et med sin kone, Brienne Elisabeth Brown.

Alle de seneste resultater handler om at minimere mængden af ​​papir, reb eller snor, der bruges til at lave en bestemt form. Schwartz' seneste løb startede med Möbius-strimlen, som er dannet ved at tage en papirstrimmel, give den et twist og samle enderne. Den har den bizarre egenskab, at den er en overflade, der kun har én side, hvilket betyder, at du kan spore hele overfladen uden nogensinde at løfte fingeren.

Helt tilbage i 1930'erne har matematikere forsøgt at finde det stumst mulige rektangel, der kan snos til en Möbius-strimmel. Det virker intuitivt klart, at det er nemt at sno et langt, tyndt rektangel til en ensidet strimmel, men at gøre det med en firkant er umuligt. Men hvor går grænsen egentlig?

Optimale former opstår, når vi forsøger at minimere eller maksimere en eller anden værdi, som i dette tilfælde forholdet mellem bredden af ​​en strimmel og dens længde. På afgørende matematiske måder er de den mest ekstreme version af en form. Studiet af optimale former er en bro mellem geometri, hvor længden betyder noget, og topologi, en gren af ​​matematik, der beskæftiger sig med idealiserede objekter, der er uendeligt strækbare og komprimerbare. I topologi er Möbius-strimler af forskellige størrelser udskiftelige, da en lille strimmel kan strækkes til en stor, en bred strimmel sammenpresses til en tynd, og så videre. Tilsvarende er rektangulære strimler af enhver størrelse alle, topologisk, de samme.

Men operationen med at sno en strimmel og forbinde enderne ændrer tingene. At regne med optimale former er at regne med topologiens grænser. Ja, du kan presse en Möbius-strimmel ind i en anden. Men hvor meget kan du presse, før det bliver umuligt at komme længere?

"Et spørgsmål er, hvad er den mindste længde, og det andet er, er der en måde at opnå den mindste længde på, og hvordan ser det ud," sagde Elizabeth Denne fra Washington og Lee University.

I alt har der været mindst fem resultater i de seneste år, der har identificeret nye bedste værdier for forskellige former, herunder Möbius-strimlen (med et snoning), den tre-snoede Möbius-strimmel og den simple knude. Nogle af disse resultater identificerer den bedst kendte værdi for en form; andre går et skridt videre og beviser, at bedre værdi ikke er mulig.

Den Optimale Möbius Strip

For at formalisere, hvor tæt på et kvadrat et rektangel er, bruger matematikere et tal kaldet aspektforholdet. Det er simpelthen længden divideret med bredden. En firkant har et billedformat på 1, mens et langt, tyndt, båndlignende rektangel har et meget større formatforhold. Det bånd har masser af slaphed, så rektanglets ender kan snoes og fastgøres til hinanden. Men efterhånden som strimlen bliver kortere, og billedformatet kommer tættere på 1 – en firkant — bliver det sværere. På et vist tidspunkt er det ikke muligt længere.

I 1977 formodede to matematikere, at for at blive snoet i en Möbius-strimmel, skal et rektangel med bredde 1 være længere end $latex sqrt{3}$, som i strimlen nederst til højre. I august 2023 beviste Schwartz, at de var korrekte: Noget tættere på en firkant end det, og der er ingen måde at sno rektanglet til en Möbius-strimmel.

Du kan blive fristet til at finde en smart løsning. Hvis du folder en firkant op som en harmonika, og skaber en tynd papirstrimmel, kan du så sno den til en Möbius-strimmel. Men det tæller ikke, for folderne er skarpe, ikke glatte. (Gladhed har en særlig matematisk betydning, der stemmer overens med den almindelige engelske betydning.)

Et centralt værktøj til at finde ud af, hvordan optimale former ser ud, kaldes en "begrænsende form." Begrænsende former adskiller sig på afgørende punkter fra de former, der optimeres, men deler også nogle af deres egenskaber. Tænk i grove træk over, hvordan hvis du strækker et rektangel ud for at gøre det længere og tyndere, begynder det at ligne en streg, eller hvordan polygoner med flere og flere sider begynder at ligne en cirkel.

I dette tilfælde skaber Schwartz en begrænsende form for Möbius-strimlen. Start med et fladt stykke papir, der er en enhed bredt og $latex sqrt{3}$ enheder langt. Begynd med at folde den ved at følge instruktionerne nedenfor. Dette vil skabe skarpe folder ligesom harmonikaens, men om et øjeblik vil vi gøre disse folder glatte ved at slappe af papiret en lille smule.

Fold ned fra øverste venstre hjørne og op fra nederste højre hjørne, så du får en diamant. Fold derefter op på tværs af diamantens midtlinje og tape de to kanter sammen, vist med blå og gule stiplede linjer, der mødes i diamantens indre. Tilføj nu bare den mindste smule slæk ved at gøre strimlen en lille smule længere eller en lille smule smallere, så du kan trække trekanterne fra hinanden. Dette er din Möbius-strimmel. En uendeligt lille myre, der rejste på overfladen af ​​trekanten og fulgte folderne, ville gå hele vejen rundt - den har kun én side.

Matematikere har længe vidst, at en sådan trekant er en begrænsende form for Möbius-strimler. Schwartz viste, at andre begrænsende former, der ville give mulighed for en stubber strimmel, ikke eksisterer. For at gøre dette brugte han "T" dannet af trekantens folder, som det ses i trekanten længst til højre ovenfor.

Schwartz kombinerede argumenter fra topologi og geometri. Han brugte topologi til at vise, at på hver papirstrimmel af Möbius er det muligt at tegne skærende linjer, der danner et T på en bestemt måde. Derefter viste han ved hjælp af en grundlæggende geometri - Pythagoras sætning og trekantsuligheden - at hvis et sådant T eksisterer (hvilket det skal), skal størrelsesforholdet af strimlen være større end $latex sqrt {3}$.

Den optimale snoede papircylinder

Efter at Schwartz havde identificeret den optimale Möbius-strimmel, spurgte folk ham: Hvad ville der ske med flere drejninger? Ethvert ulige antal snoninger producerer en Möbius-strimmel, fordi den resulterende form stadig kun har én side. På den anden side giver et lige antal drejninger en tosidet struktur kaldet en snoet cylinder (vist nedenfor til venstre). I modsætning til en almindelig cylinder har den ikke en veldefineret inderside og yderside.

Efter hans papir om Möbius-striben, Schwartz bevist i slutningen af ​​september, at den begrænsende form af den snoede cylinder kan laves ved at folde et 1 x 2 rektangel dannet af fire stablede ret ligebenede trekanter (som vist ovenfor til højre). For at begynde skal du folde trekant B bag trekant A og trekant D over trekant C. (Pile med stiplede linjer angiver folder, der går bagud, og solide pile angiver folder i fremadgående retning). Fold derefter den resulterende trekant i to ved at sætte den nederste halvdel bag den øverste halvdel. Tape derefter de stiplede blå og gule linjer sammen (som oprindeligt var toppen og bunden af ​​rektanglet). Til sidst skal du gøre startrektanglet lige en smule længere, så du har nok slæk til at trække den flade form op i en sammenpresset, snoet cylinder. "Den grundlæggende idé er først at bygge den begrænsende form og derefter slappe lidt af i formen og runde folderne ud," skrev Schwartz. "Jeg tænker på det her som lidt ligesom at lave tingen og derefter lægge den i blød natten over i vand." Som du kan se på figuren (ovenfor til højre), er den stablede trekantform dobbelt så lang som den er bred, så det optimale billedformat for den snoede cylinder er 2.

Den optimale Möbius-strimmel med tre snoninger

Schwartz vendte derefter sin opmærksomhed mod den tre-snoede Möbius-strimmel. Ligesom en-twist-strimlen er dette en ensidet figur, men på grund af de to ekstra snoninger er dens grænse mere kompliceret. Schwartz troede, at dens begrænsende form ville være hexaflexagon, en forvirrende form populær af Martin Gardner i en 1956 kolonne in Scientific American. Hexaflexagoner laves ved at folde en strimmel ligesidede trekanter og lime enderne sammen. En fladtrykt sekskant ligner en sekskant opdelt i seks trekanter. Men det kan "bøjes" ved at klemme tilstødende sider sammen, som i børnespil MASH. Når den åbnes igen, vender et andet sæt trekanter udad. "Denne ting er ligesom hvis en spåmand og et Möbius-band fik en baby," sagde Schwartz.

Men Schwartz' kone, Brienne Elisabeth Brown, begyndte selv at lege med papir og afslørede, at hexaflexagon var "lidt af en rød sild," sagde Schwartz. Brown fandt en konstruktion, hun kalder "krysset" (vist nedenfor), der er en begrænsende form af en tre-snoet Möbius-strimmel og er tre gange så lang som den er bred. Først folder du langs den diagonale linje i midten af ​​strimlen, idet du tager den nederste del foran den øverste del. Derefter folder du den øverste højre trekant foran trekanten under og til venstre. Du har nu formen vist i trin 2: et skrå parallelogram med en firkant, der stikker ud til højre. Bring firkanten bag parallelogrammet og trekanten øverst foran den firkant, der nu er under den. Dette laver en ny firkant, vist i trin 3.

Hvad der oprindeligt var den øverste og nederste kant (vist med stiplede blå og gule linjer) er nu begge på venstre kant af firkanten; tape dem sammen, og du har skabt en begrænsende form for en Möbius-strimmel med tre snoninger. Som i tilfældet med one-twist-strimlen, er denne flade form ikke i sig selv en Möbius-strimmel, men hvis den får bare lidt ekstra længde, så den kan slappe af i tre dimensioner uden skarpe bøjninger, vil den danne en tre-snoet strimmel.

Brown og Schwartz fandt også en helt anden begrænsende form for tre-vrid cylinderen, som de kalder koppen. I modsætning til på kryds og tværs kan koppen ikke fås til at ligge fladt. Men ligesom krydset er den tre gange så lang, som den er bred. I et papir indsendt den 16. oktober forklarer Brown og Schwartz, hvorfor de mener, at den optimale tre-snoede strimmel har et billedformat på 3. Men de har endnu ikke været i stand til at bevise det, blandt andet fordi koppens eksistens, som ikke kan være fladtrykt, betyder, at den slags argumenter, Schwartz fremførte i et- og to-vrid-tilfældene, ikke kan udvides til at omfatte tre-vrid-sagen.

Optimale Trefoil Knob

Ikke alle optimale former er varianter på Möbius-strimlen. Matematikere overvejer også, hvor meget materiale du skal bruge for at lave forskellige slags knob. I 2020, this og to af hendes bachelorstuderende - John Carr Haden og Troy Larsen - studerede knuder, der kan tegnes på overfladen af ​​en torus eller doughnut.

Den enkleste torusknude - ja, den enkleste ikke-trivielle knude, punktum - kaldes en trefoil. Det er ligesom den, mange mennesker bruger i det første trin med at binde deres snørebånd ved at lave en løkke i et stykke reb og trække den ene ende igennem, hvis de i stedet for derefter at binde en sløjfe, bare limede spidserne af snørebåndene sammen for at danne en overhåndsknude med de to løse ender forbundet.

Den sædvanlige måde at binde trefoil på svarer til at vikle et stykke snor rundt om torusen som vist her: