Nyt prøvetræk tråder nålen på et problem med klæbrig geometri | Quanta Magasinet

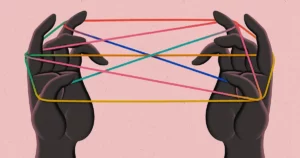
I 1917 poserede den japanske matematiker Sōichi Kakeya, hvad der i første omgang virkede som intet andet end en sjov øvelse i geometri. Læg en uendelig tynd, tommer lang nål på en flad overflade, og drej den derefter, så den peger i hver retning efter tur. Hvad er det mindste område, nålen kan feje ud?

Hvis du blot drejer den rundt om midten, får du en cirkel. Men det er muligt at flytte nålen på opfindsomme måder, så du får meget mindre plads. Matematikere har siden stillet en beslægtet version af dette spørgsmål, kaldet Kakeya-formodningen. I deres forsøg på at løse det har de afsløret overraskende forbindelser til harmonisk analyse, talteori og endda fysik.

"På en eller anden måde er denne geometri af linjer, der peger i mange forskellige retninger, allestedsnærværende i en stor del af matematik," sagde jonathan hickman fra University of Edinburgh.

Men det er også noget, matematikere stadig ikke helt forstår. I de sidste par år har de bevist variationer af Kakeya-formodningen i lettere indstillinger, men spørgsmålet forbliver uløst i det normale, tredimensionelle rum. I nogen tid virkede det, som om alle fremskridt var gået i stå på den version af formodningen, selvom det har adskillige matematiske konsekvenser.

Nu har to matematikere så at sige flyttet nålen. Deres nye bevis rammer en stor forhindring der har stået i årtier - genopliver håbet om, at en løsning endelig kan være i sigte.

Hvad er Small Deal?

Kakeya var interesseret i sæt i planet, der indeholder et linjestykke med længde 1 i hver retning. Der er mange eksempler på sådanne sæt, det enkleste er en skive med en diameter på 1. Kakeya ville vide, hvordan det mindste sådant sæt ville se ud.

Han foreslog en trekant med let indhulede sider, kaldet en deltoid, som har halvdelen af ​​skivens areal. Det viste sig dog, at det er muligt at gøre meget, meget bedre.

I 1919, blot et par år efter, at Kakeya stillede sit problem, viste den russiske matematiker Abram Besicovitch, at hvis man arrangerer sine nåle på en helt særlig måde, kan man konstruere et tornet udseende sæt, der har et vilkårligt lille område. (På grund af XNUMX. verdenskrig og den russiske revolution ville hans resultat ikke nå resten af ​​den matematiske verden i en årrække.)

For at se, hvordan dette kan fungere, skal du tage en trekant og dele den langs bunden i tyndere trekantede stykker. Skub derefter disse stykker rundt, så de overlapper så meget som muligt, men stikker ud i lidt forskellige retninger. Ved at gentage processen igen og igen - opdele din trekant i tyndere og tyndere fragmenter og omhyggeligt omarrangere dem i rummet - kan du gøre dit sæt så lille, som du vil. I den uendelige grænse kan du opnå et sæt, der matematisk ikke har noget areal, men som stadig paradoksalt nok kan rumme en nål, der peger i enhver retning.

"Det er lidt overraskende og kontraintuitivt," sagde Ruixiang Zhang fra University of California, Berkeley. "Det er et sæt, der er meget patologisk."

Dette resultat kan generaliseres til højere dimensioner: Det er muligt at konstruere et sæt med vilkårligt lille volumen, der indeholder et enhedslinjesegment, der peger i alle retninger i n-dimensionelt rum.

Besicovitch så ud til at have løst Kakeyas spørgsmål fuldstændigt. Men årtier senere begyndte matematikere at arbejde på en anden version af problemet, hvor de erstattede areal (eller volumen, i det højere-dimensionelle tilfælde) med en anden opfattelse af størrelse.

For at forstå denne omformulering af spørgsmålet skal du først tage hvert linjesegment i et Kakeya-sæt og fedte det lidt op - som om du brugte en egentlig nål i stedet for en idealiseret. I flyet vil dit sæt bestå af ekstremt tynde rektangler; i tredimensionelt rum vil du have en samling ekstremt tynde rør.

Disse fede sæt har altid et eller andet areal (eller volumen, men vi holder os til den todimensionelle sag indtil videre). Når du ændrer bredden på din nål, ændres dette område. I 1970'erne viste matematikeren Roy Davies (der døde i sidste måned), at hvis det samlede areal ændres med en lille mængde, må bredden af ​​hver nål ændre sig drastisk. For eksempel, hvis du vil have en opfedet version af Besicovitch's sæt til at have et areal på 1/10 kvadrattomme, skal hver nål have en tykkelse på omkring 0.000045 tomme: e^-10 en tomme, for at være præcis. Men hvis du ville gøre det samlede areal 1/100 af en kvadrattomme - 10 gange mindre - skulle nålen være e^-100 en tomme tyk. (Treogfyrre nuller følger decimaltegnet, før du kommer til de andre cifre.)

"Hvis du fortæller mig, hvor lille du vil have området skal være, så er jeg nødt til at kræve en nål, som bare er utrolig tynd," sagde Charles Fefferman fra Princeton University.

Matematikere måler "størrelsen" af Kakeya-sættet ved hjælp af en størrelse kaldet Minkowski-dimensionen, som er relateret til, men ikke helt det samme som en almindelig dimension (defineret som antallet af uafhængige retninger, du skal bruge for at beskrive et rum).

Her er en måde at tænke på Minkowski-dimensionen: Tag dit sæt og dæk det med små kugler, der hver har en diameter på en milliontedel af din foretrukne enhed. Hvis dit sæt er et linjestykke med længde 1, skal du bruge mindst 1 million bolde til at dække det. Hvis dit sæt er et kvadrat med område 1, har du brug for mange, mange flere: en million kvadrat eller en billion. For en kugle med volumen 1 er den omkring 1 million terninger (en kvintillion) og så videre. Minkowski-dimensionen er værdien af ​​denne eksponent. Den måler den hastighed, hvormed antallet af kugler, du skal bruge for at dække dit sæt, vokser, efterhånden som diameteren af ​​hver kugle bliver mindre. Et linjestykke har dimension 1, et kvadrat har dimension 2, og en terning har dimension 3.

Disse dimensioner er velkendte. Men ved at bruge Minkowskis definition bliver det muligt at konstruere et sæt, der har en dimension på f.eks. 2.7. Selvom et sådant sæt ikke fylder tredimensionelt rum, er det på en eller anden måde "større" end en todimensionel overflade.

Når du dækker et sæt med bolde med en given diameter, nærmer du dig volumen af ​​den opfedede version af sættet. Jo langsommere mængden af ​​sættet falder med størrelsen på din nål, jo flere kugler skal du bruge for at dække det. Du kan derfor omskrive Davies' resultat - som siger, at arealet af et Kakeya-sæt i planet falder langsomt - for at vise, at sættet skal have en Minkowski-dimension på 2. Kakeya-formodningen generaliserer denne påstand til højere dimensioner: Et Kakeya-sæt skal altid have samme dimension som det rum, det bebor.

Det simple udsagn har været overraskende svært at bevise.

Et tårn af formodninger

Indtil Fefferman lavede en opsigtsvækkende opdagelse i 1971 blev formodningen betragtet som en kuriosum.

Han arbejdede på et helt andet problem på det tidspunkt. Han ønskede at forstå Fourier-transformationen, et kraftfuldt værktøj, der gør det muligt for matematikere at studere funktioner ved at skrive dem som summer af sinusbølger. Tænk på en musikalsk node, som består af masser af overlappende frekvenser. (Det er grunden til, at et mellem C på et klaver lyder anderledes end et mellem C på en violin.) Fourier-transformationen gør det muligt for matematikere at beregne de konstituerende frekvenser af en bestemt tone. Det samme princip virker for lyde så komplicerede som menneskelig tale.

Matematikere vil også gerne vide, om de kan genopbygge den oprindelige funktion, hvis de kun får nogle af dens uendeligt mange konstituerende frekvenser. De har en god forståelse for, hvordan man gør dette i én dimension. Men i højere dimensioner kan de træffe forskellige valg om, hvilke frekvenser de skal bruge, og hvilke de skal ignorere. Fefferman beviste, til sine kollegers overraskelse, at man måske ikke kunne genopbygge sin funktion, når man stolede på en særlig velkendt måde at vælge frekvenser på.

Hans bevis var afhængig af at konstruere en funktion ved at modificere Besicovitchs Kakeya-sæt. Dette inspirerede senere matematikere til at udvikle et hierarki af formodninger om Fourier-transformationens højere dimensionelle adfærd. I dag inkluderer hierarkiet endda formodninger om adfærden af ​​vigtige partielle differentialligninger i fysik, som Schrödinger-ligningen. Hver formodning i hierarkiet antyder automatisk den, der er under den.

Kakeya-formodningen ligger i bunden af ​​dette tårn. Hvis det er falsk, så er udsagnene også højere i hierarkiet. På den anden side vil bevis for, at det er sandt, ikke umiddelbart indebære sandheden af ​​de formodninger, der er placeret over det, men det kan give værktøjer og indsigt til at angribe dem.

“Det fantastiske ved Kakeya-formodningen er, at det ikke kun er et sjovt problem; det er en rigtig teoretisk flaskehals,” sagde Hickman. "Vi forstår ikke mange af disse fænomener i partielle differentialligninger og Fourier-analyse, fordi vi ikke forstår disse Kakeya-sæt."

Udklække en plan

Feffermans bevis - sammen med efterfølgende opdagede forbindelser til talteori, kombinatorik og andre områder - genoplivede interessen for Kakeya-problemet blandt topmatematikere.

I 1995 beviste Thomas Wolff, at Minkowski-dimensionen af ​​et Kakeya-sæt i 3D-rum skal være mindst 2.5. Den nedre grænse viste sig at være svær at øge. Så, i 1999, matematikerne Nets Katz, Izabella Łaba , Terence tao formåede at slå den. Deres nye bund: 2.500000001. På trods af hvor lille forbedringen var, overvandt den en massiv teoretisk barriere. Deres papir var offentliggjort i Annals of Mathematics, feltets mest prestigefyldte tidsskrift.

Katz og Tao håbede senere at kunne anvende nogle af ideerne fra det arbejde til at angribe 3D Kakeya-formodningen på en anden måde. De antog, at ethvert modeksempel skal have tre særlige egenskaber, og at sameksistensen af ​​disse egenskaber må føre til en modsigelse. Hvis de kunne bevise dette, ville det betyde, at Kakeya-formodningen var sand i tre dimensioner.

De kunne ikke gå hele vejen, men de gjorde nogle fremskridt. Især viste de (sammen med andre matematikere), at ethvert modeksempel skal have to af de tre egenskaber. Det skal være "plany", hvilket betyder, at når linjestykker skærer hinanden i et punkt, ligger disse segmenter også næsten i samme plan. Det skal også være "kornet", hvilket kræver, at planene for nærliggende skæringspunkter er tilsvarende orienteret.

Det efterlod den tredje ejendom. I et "sticky" sæt skal linjestykker, der peger i næsten samme retning, også være placeret tæt på hinanden i rummet. Katz og Tao kunne ikke bevise, at alle modeksempler måtte være klæbrige. Men intuitivt virker et klæbrigt sæt som den bedste måde at tvinge en masse overlap mellem linjesegmenterne og derved gøre sættet så lille som muligt - præcis hvad du har brug for for at skabe et modeksempel. Hvis nogen kunne vise, at et klæbrigt Kakeya-sæt havde en Minkowski-dimension på mindre end 3, ville det modbevise 3D Kakeya-formodningen. "Det lyder som om 'klæbende' ville være det mest bekymrende tilfælde," sagde Larry Guth fra Massachusetts Institute of Technology.

Det er ikke længere en bekymring.

Klæbepunktet

I 2014 - mere end et årti efter Katz og Tao forsøgte at bevise Kakeya-formodningen - Tao opslået en oversigt over deres tilgang på sin blog, hvilket giver andre matematikere mulighed for selv at prøve det.

I 2021, blev Hong Wang, en matematiker ved New York University, og Joshua Zahl fra University of British Columbia besluttede at fortsætte, hvor Tao og Katz var slap.

De startede med at antage eksistensen af ​​et klæbrigt modeksempel med en Minkowski-dimension på mindre end 3. De vidste fra tidligere arbejde, at et sådant modeksempel skulle være fladt og kornet. "Så vi var i den slags verden, som Terry Tao og Nets Katz tænkte på," sagde Zahl. Nu skulle de vise, at de plane, kornede og klæbrige egenskaber spillede ud af hinanden og førte til en modsigelse, som ville betyde, at dette modeksempel faktisk ikke kunne eksistere.

For at få den modsigelse vendte Wang og Zahl imidlertid deres opmærksomhed i en retning, som Katz og Tao ikke havde forudset - mod et område kendt som projektionsteori.

De startede med at analysere strukturen af ​​deres klæbrige modeksempel mere detaljeret. Hvis du overvejer den idealiserede version af sættet, har det et uendeligt antal linjesegmenter, der peger i alle retninger. Men i dette problem skal du huske, at du har at gøre med opfedede versioner af disse linjesegmenter - en flok nåle. Hver af disse nåle kan indeholde mange af de idealiserede linjesegmenter, hvilket betyder, at du kan kode hele det uendelige sæt med et begrænset antal nåle. Afhængigt af hvor tykke nålene er, kan dit fedtede sæt se meget anderledes ud.

Hvis sættet er klistret, vil det se nogenlunde ens ud, uanset hvor tykke nålene er.

Wang og Zahl brugte denne egenskab til at vise, at når nålene bliver tyndere, bliver sættet mere og mere plan. Gennem denne proces kunne de "udtrække et endnu mere patologisk objekt," sagde Zahl - noget, der så ud til at have umulige kvaliteter.

Det var det, de viste næste gang. De beviste, at dette patologiske objekt skulle se ud på en af ​​to måder, som begge førte til modsigelser. Enten ville du være i stand til at projicere det ned i 2D-rummet på en måde, der gjorde det meget mindre i mange retninger - noget som Wang og hendes kolleger netop havde vist sig umuligt. Eller i det andet tilfælde ville nålene i sættet være organiseret efter en meget specifik slags funktion, som Zahl og hans samarbejdspartnere for nylig havde bevist kunne ikke eksistere, fordi det ville føre til andre former for projektioner, der ikke gav mening.

Wang og Zahl havde nu deres modsigelse - hvilket betyder, at der ikke er nogen klæbrige modeksempler på Kakeya-formodningen. (De viste dette ikke kun for Minkowski-dimensionen, men også for en beslægtet størrelse kaldet Hausdorff-dimensionen.) "Resultatet udelukker hele denne klasse af modeksempler," sagde Zahl - den nøjagtige type af mængder, matematikere havde anset for mest sandsynligt at modbevise. formodningen.

Det nye værk "er stærk støtte til, at Kakeya-formodningen er sand," sagde Pablo Shmerkin fra University of British Columbia. Selvom det kun gælder for det tredimensionelle tilfælde, kan nogle af dets teknikker være nyttige i højere dimensioner. Efter at have brugt år på at gøre fremskridt med formodningerne i andre talsystemer, er matematikere begejstrede over denne tilbagevenden til problemets oprindelige domæne med reelle tal.

"Det er bemærkelsesværdigt, at de løste denne sag fuldstændigt," sagde Zhang. "I de virkelige omgivelser er det ekstremt sjældent." Og hvis nogen kan bevise, at et modeksempel må være klistret, vil det nye resultat antyde den fulde formodning i tre dimensioner. Hierarkiet af formodninger bygget over det vil så forblive sikkert, dets fundament stabilt.

"På en eller anden måde passer disse to forskellige problemer i projektionsteorien, som på forsiden ikke har meget med hinanden at gøre, ganske fint sammen for at give præcis det, der var nødvendigt for Kakeya," sagde Zahl.